線形回帰の理論的な深堀り
Deep dive into the theory of linear regression.
線形回帰の背後にある理由と、様々な方法で自然に拡張する方法を学ぶ
ほとんどのデータサイエンスのアスピリングブロガーが行うこと:線形回帰に関する入門記事を書くことです。このモデルは、この分野に入ると最初に学ぶものの一つであるため、自然な選択肢です。これらの記事は初心者には素晴らしいものですが、ほとんどの場合、シニアデータサイエンティストを満足させるには十分に深くはありません。
そこで、線形回帰についてのあまり知られていないが、新鮮な詳細をいくつかご案内します。これらは、あなたをより良いデータサイエンティストにし(そして面接中にボーナスポイントを与えます)。
この記事はかなり数学的なので、追跡するためには、確率と微積分についての堅固な基礎を持っていることが有益です。
データ生成プロセス
モデリングするときに、データ生成プロセスについて考えることが好きです。ベイジアンモデリングに取り組んだことがある人は、私が何を意味するか知っていますが、その他の人のために説明します:データセット( X 、 y )は、サンプル( x 、 y )で構成されています。 x が与えられた場合、目標の y にどのように到達できますか?
- GPTとBERT:どちらが優れているのか?
- DeepMind RoboCat:自己学習ロボットAIモデル
- BITEとは 1枚の画像から立ち姿や寝そべりのようなポーズなど、困難なポーズでも3D犬の形状とポーズを再構築する新しい手法
n個のデータポイントがあり、各 x にはk個のコンポーネント/特徴があると仮定してみましょう。
係数w₁、…、wₖ(係数)、b(切片)、σ(ノイズ)を持つ線形モデルの場合、データ生成プロセスは次のようになります。
- µ = w₁x₁ + w₂x₂ + … + wₖxₖ + bを計算します。
- ランダムにy〜N(µ、σ²)をロールします。これは他のランダムに生成された数とは独立しています。代替方法:ε〜N(0、σ²)をロールし、y = µ + ε を出力します。
これで十分です。これらの2つの単純な行は、人々が長々と説明することが好きな最も重要な線形回帰の仮定、すなわち線形性、同分散性、およびエラーの独立性に相当します。
プロセスのステップ1からもわかるように、私たちは実際のターゲットではなく、典型的な線形方程式w₁x₁ + w₂x₂ + … + wₖxₖ + bで期待値µをモデル化しています。私たちはどちらにせよターゲットを命中させないことを知っているため、yを生成する分布の平均値に落ち着くことになります。
拡張
一般化線形モデル。データ生成プロセスに正規分布を使用する必要はありません。 正のターゲットのみを含むデータセットを扱う場合、ポアソン 分布 Poi(µ)を使用することが有益である場合があります。これにより、ポアソン回帰が得られます。
データセットにはターゲット0と1のみが含まれている場合は、p = sigmoid(µ)であるベルヌーイ分布 Ber(p)を使用し、et voilà: ロジスティック回帰が得られます。
0、1、…、nの間の数字のみですか? 二項分布を使用して、二項回帰を取得します。
リストは続きます。長い話を短くすると:
データで観察されるラベルを生成できる分布について考えてください。
実際に最小化しているものは何ですか?
よし、モデルを決めました。それでは、どのようにトレーニングし、パラメータを学習しますか?もちろん、あなたは知っています:(平均)二乗誤差を最小限に抑えました。しかし、なぜですか?
秘密は、先に説明した生成プロセスを使用して、計画的に最大尤度推定を行うだけだからです。私たちが観測するラベルは、すべて独立してµ₁、µ₂、…、µₙの平均を持つ正規分布によって生成されたy₁、y₂、…、yₙです。これらのyを見る可能性は何ですか?それは以下のとおりです。
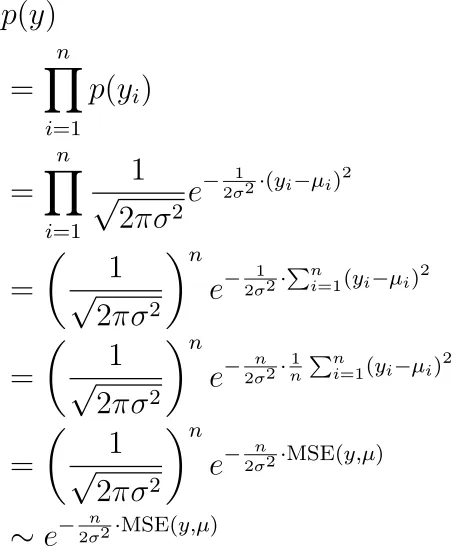
今度は、この項目を最大化するパラメータ(µᵢの中に隠れている)を見つけたいと思います。これは、平均二乗誤差を最小化することと同じです。
拡張
等分散ではない。実際、σは一定である必要はありません。データセット内の各観測値に異なるσᵢを持つことができます。その場合、代わりに
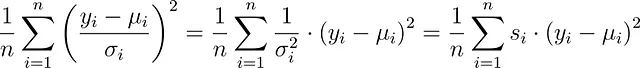
に最小化することができます。これは、サンプル重み付き最小二乗法です。モデリングライブラリには、これらの重みを設定できるようにする機能が通常あります。たとえば、scikit-learnでは、fit関数のsample_weightキーワードを設定できます。
これにより、対応するsを増やすことで、特定の観測値に重点を置くことができます。これは、分散σ²を減らすことに相当し、つまり、この観測値の誤差が小さいことについてより自信を持っているということです。この方法は重み付き最小二乗法とも呼ばれます。
入力に依存する分散。分散は入力xにも依存すると言えます。この場合、分散減衰とも呼ばれる興味深い損失関数が得られます:

全体の導出プロセスはこちらに概要が記載されています:
回帰ニューラルネットワークで不確実性の推定を無料で取得する
適切な損失関数が与えられた場合、標準ニューラルネットワークでも不確実性を出力できます
towardsdatascience.com
正則化。観測ラベルy₁、y₂、…、yₙの尤度だけを最大化するのではなく、ベイズ的な立場を取り、事後尤度を最大化することができます。
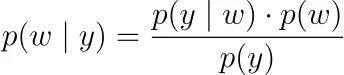
ここで、p(y | w)は上記の尤度関数です。p(w)に対して確率密度を決定する必要があります。これを事前分布または事前分布と呼びます。パラメータが0を中心に独立して正規分布すると言うと、つまり、wᵢ〜N(0, ν²)とすると、L2正則化、つまりリッジ回帰が得られます。ラプラス分布の場合、L1正則化、つまりLASSOが得られます。
なぜそうなのでしょうか?正規分布を例にとってみましょう。私たちは次のようになります。
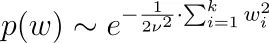
したがって、上記のp(y | w)の式と一緒に、次を最大化する必要があります。
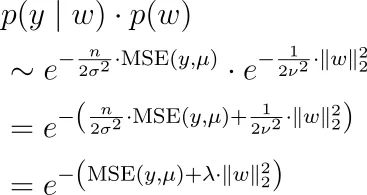
つまり、平均二乗誤差に加えて正則化ハイパーパラメーターのL2ノルムを掛けたものを最小化する必要があります。
ベイズの公式から、wに依存しない分母p(y)を落としたことに注意してください。したがって、最適化のために無視することができます。
パラメータの事前分布として他の分布を使用して、より興味深い正則化を作成することができます。パラメータwが正規分布であり、いくつかの相関行列Σと相関していると言うことさえできます。
Σが正定値であると仮定しましょう。そうでない場合、密度p(w)はありません。
数学をすると、次のように最適化する必要があることがわかります。
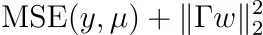
行列Γのために最適化する必要があります。 注:Γは可逆であり、Σ⁻¹=ΓᵀΓとなります。 これはまた、Tikhonov正則化とも呼ばれます。
ヒント:次のことから始めてください。
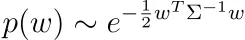
そして、正定値行列は可逆行列とその転置行列の積に分解できることを覚えておいてください。
損失関数を最小化する
素晴らしい、私たちはモデルを定義し、最小化するための最良のパラメータを学習する方法を知っています。しかし、どのように最適化し、つまり損失関数を最小化する最良のパラメータを学習できますか?そして、一意の解があるのはいつですか?調べてみましょう。
最小二乗法
正則化を行わず、サンプルの重みを使用しないと仮定しましょう。その場合、MSEは次のように書くことができます。
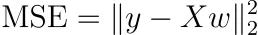
これはかなり抽象的ですので、別の方法で書いてみましょう。
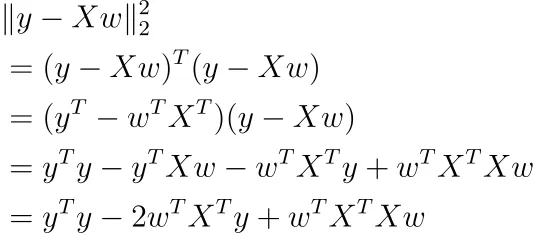
行列微積分を使用すると、この関数のwに関する微分を取ることができます(バイアス項bが含まれていると仮定しています)。
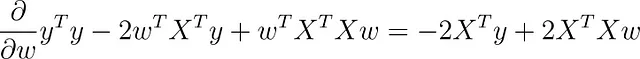
この勾配をゼロに設定すると、次のようになります。
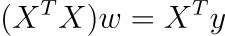
(n×k)行列Xがランクkである場合、(k×k)行列XᵀXもランクkであるため、それは可逆です。なぜでしょうか?rank(X)=rank(XᵀX)からわかります。
この場合、私たちは唯一の解を得ます。
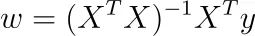
注:ソフトウェアパッケージはこのように最適化しませんが、勾配降下法またはその他の反復技術を使用するため、より速くなります。それでも、この式は素敵であり、問題に関するいくつかの高レベルな洞察を提供してくれます。
しかし、これは本当に最小値なのでしょうか?Hessianを計算することで、それを確認できます。HessianはX ᵀ Xであり、任意のwに対してw ᵀ X ᵀ Xw = |Xw|² ≥ 0であるため、行列は正半定義的です。X ᵀ Xが可逆であるため、つまり0が固有ベクトルではないため、それは厳密に正定義的です。したがって、私たちの最適なwは、私たちの問題を最小化していることになります。
完全多重共線性
これはフレンドリーなケースでした。しかし、Xのランクがkよりも小さい場合はどうなるでしょうか?これは、データセットに2つの特徴があり、1つが他の特徴の倍数である場合に起こる可能性があります。たとえば、私たちのデータセットで高さ(m単位)と高さ(cm単位)の特徴を使用する場合、高さ(cm単位)= 100 *高さ(m単位)となります。
また、カテゴリデータをワンホットエンコードし、列の1つを削除しない場合にも発生する可能性があります。たとえば、データセットに赤、緑、または青という色の特徴がある場合、ワンホットエンコードしてcolor_red、color_green、color_blueの3つの列が残ります。これらの特徴では、color_red + color_green + color_blue = 1であり、完全多重共線性を誘発します。
これらの場合、X ᵀ Xのランクもkよりも小さくなるため、この行列は可逆ではありません。
物語の終わり。
それとも違うのかもしれません。実際には、2つのことを意味する可能性があります:( X ᵀ X ) w = X ᵀ yには
- 解が存在しない場合、または
- 無限の解が存在する場合。
これは、Moore-Penrose逆を使用して1つの解を得ることができるということがわかりました。これは、無限に多くの解がある場合であり、それらすべてが同じ(トレーニング)平均二乗誤差損失を与えます。
行列AのMoore-Penrose逆をA ⁺で示すと、線形方程式を解くことができます。
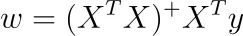
X ᵀ Xのヌル空間をこの特定の解に追加すると、他に無限に多くの解を得ることができます。
Tikhonov正則化による最小化
重みに事前分布を追加することができることを思い出してください。その場合、いくつかの可逆行列Γに対して、最小化する必要がありました。
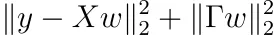
通常の最小二乗法と同じ手順に従って、つまりwに関して導関数を取り、その結果をゼロに設定することで、解を得ることができます。
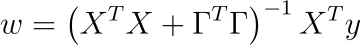
素敵な部分:
XᵀX + ΓᵀΓは常に可逆です!
なぜかを調べてみましょう。X ᵀ X + ΓᵀΓのヌル空間が{0}だけであることを示せば十分です。したがって、( X ᵀ X + ΓᵀΓ) w = 0となるwを取ります。今、私たちの目標は、w = 0を示すことです。
( X ᵀ X + ΓᵀΓ) w = 0から、
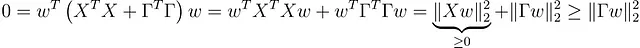
が導かれ、これは |Γ w | = 0 → Γ w = 0 を意味します。Γが可逆であるため、wは0でなければなりません。同じ計算を使用して、Hessianも正定義的であることがわかります。
素晴らしい、Tikhonov正則化が自動的に解を一意にするのに役立ちます!Ridge回帰はTikhonov回帰の特殊な場合であり(Γ = λ Iₖの場合、Iₖはk次元の単位行列)、同じことが当てはまります。
サンプルの重み付けの追加
最後に、Tikhonov正則化にサンプルの重み付けを追加しましょう。サンプル重み付けを追加することは、
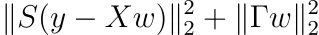
正の対角エントリsᵢを持つ対角行列Sについてのものです。最小化は通常の最小二乗法の場合と同様に簡単です。結果は以下の通りです。
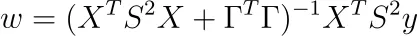
注意:ヘッセ行列も正定値です。
あなたの宿題
Tikhonov正則化の場合、重みが0を中心に置く必要はなく、他の点w₀に置くことができると仮定します。最適化問題が以下のようになることを示しましょう。
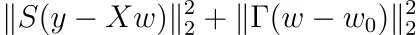
そして、その解決策は以下の通りです。
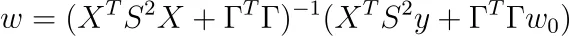
これはTikhov正則化の最も一般的な形式です。ここではP := S²、Q := ΓᵀΓと定義する人がいます。
まとめ
この記事では、線形回帰のいくつかの高度な側面について紹介しました。生成モデルを採用することで、一般化線形モデルは通常の線形モデルと異なるのは、サンプリングされるターゲットyの分布のタイプだけであることがわかりました。
次に、平均二乗誤差を最小化することが、観測値の尤度を最大化することと等価であることを見ました。学習可能なパラメータに事前正規分布を課すと、Tikhonov(およびL2を特殊な場合として)正則化になります。Laplace分布など、異なる事前分布を使用することもできますが、その場合は解決策の閉形式がありません。それでも、凸計画アプローチを使用することで最適なパラメータを見つけることができます。
最後に、考慮された各最小化問題に対して多くの直接的な解決策の公式を見つけました。これらの式は大規模なデータセットの場合には通常使用されませんが、解決策が常に一意であることがわかりました。そして、私たちはいくつかの微積分を学んだ。😉
今日、新しい、興味深く、かつ価値のあることを学んでいただけたことを願っています。読んでいただきありがとうございました!
最後に、もし
- 私が機械学習についてもっと書くことをサポートしたい場合、そして
- VoAGIのサブスクリプションを取得する予定がある場合、
なぜこのリンクを介してそれをしないのですか?それは私をとても助けることになります! 😊
透明性を保つために、あなたにとっての価格は変わりませんが、サブスクリプション料金の約半分が直接私に送金されます。
サポートを検討していただける場合は、ありがとうございます!
何か質問があれば、LinkedInで私に書いてください!
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles





