「音のシンフォニーを解読する：音楽工学のためのオーディオ信号処理」

Decoding the Symphony of Sound Audio Signal Processing for Music Engineering

Pythonを使った時間と周波数領域の音声特徴抽出の究極ガイド

イメージ by OpenClipart-Vectors from Pixabay

はじめに
時間領域の特徴抽出 2.1 オーディオ信号処理の基礎: フレームサイズとホップ長さ 2.2 特徴1: 振幅包絡2.3 特徴2: ルート平均二乗エネルギー 2.4 特徴3: クレストファクター2.5 特徴4: ゼロクロス数
周波数領域の特徴抽出3.1 特徴5: 帯域エネルギー比3.2 特徴6: スペクトル重心3.3 特徴7: スペクトル帯域幅3.4 特徴8: スペクトルフラットネス
結論
参考文献

はじめに

情報時代において、さまざまなデータを処理し分析して実用的な知見を得る能力は、最も重要なスキルの一つです。データは私たちの周りにあります。読む本から観る映画、Instagramでいいねをする投稿、聴く音楽まで。この記事では、オーディオ信号処理の基礎を理解しようとします。

コンピューターがオーディオ信号を読む方法は？
時間領域と周波数領域の特徴とは何か？
これらの特徴はどのように抽出されるのか？
なぜこれらの特徴を抽出する必要があるのか？

特に、以下の特徴について詳細に説明します：

時間領域の特徴：振幅包絡、ルート平均二乗エネルギー、クレストファクター（およびピークから平均電力比）、ゼロクロス数。
周波数領域の特徴：帯域エネルギー比、スペクトル重心、スペクトル帯域幅（拡がり）、スペクトルフラットネス。

この記事では、音楽楽器（アコースティックギター、ブラス、ドラムセット）のオーディオ信号からこれらの特徴を抽出するための理論とPythonコードをゼロから説明します。使用するサンプルオーディオデータファイルはこちらからダウンロードできます：https://github.com/namanlab/Audio-Signal-Processing-Feature-Extraction

コード全体は上記のリポジトリで利用可能であり、また次のリンクからアクセスできます：https://github.com/namanlab/Audio-Signal-Processing-Feature-Extraction/blob/main/Audio_Signal_Extraction.ipynb

時間領域の特徴抽出

まず、音とは何か、私たちがそれをどのように知覚するのかを思い出してみましょう。高校の授業から覚えている人もいるかもしれませんが、音は振動の伝播です。音の発生によって周囲の空気分子が振動し、圧縮（高圧）と希薄化（低圧）の交互の領域が現れます。これらの圧縮と希薄化は音を伝え、私たちの耳に届き、私たちが音を知覚することを可能にします。したがって、音の伝播には時間の経過に伴うこれらの圧力変動の伝達が関与します。音の時間領域表現では、時間の異なる区間でこれらの圧力変動を捉え、分析することによって、音波を離散的な時間点でサンプリングすることで実現します（通常はデジタルオーディオ録音技術を使用）。各サンプルは特定の瞬間の音圧レベルを表します。これらのサンプルをプロットすることにより、時間の経過に伴う音圧レベルの変化が表示される波形が得られます。横軸は時間を、縦軸は音の振幅または強度を表し、通常は-1から1の間にスケーリングされます。正の値は圧縮を示し、負の値は希薄化を示します。これにより、音波の特性（振幅、周波数、持続時間など）の視覚的な表現が可能になります。

Pythonを使用して特定のオーディオの波形を抽出するためには、まず必要なパッケージを読み込むことから始めます：

import numpy as npimport matplotlib.pyplot as pltimport librosaimport librosa.displayimport IPython.display as ipdimport scipy as spp

NumPyは、配列と行列の処理や操作に関する人気のあるPythonパッケージです。線形代数から多くのタスクを簡単にするためのさまざまなツールが含まれています！

librosaは、オーディオ処理と解析のためのPythonパッケージであり、さまざまな種類のオーディオ特徴を簡単に利用できるようにするいくつかの関数とツールが含まれています。前述のように、3つの異なる楽器（アコースティックギター、ブラス、ドラムセット）の波形を分析します。オーディオファイルは以前共有されたリンクからダウンロードしてローカルリポジトリにアップロードしてください。オーディオファイルを再生するためには、IPython.displayを使用します。以下にコードを示します：

# オーディオファイルを再生する# 音声ファイルへの相対/絶対パスが正しいことを確認してください。
acoustic_guitar_path = "acoustic_guitar.wav"
ipd.Audio(acoustic_guitar_path)
brass_path = "brass.wav"
ipd.Audio(brass_path)
# 音量を低くしてください！
drum_set_path = "drum_set.wav"
ipd.Audio(drum_set_path)

次に、librosaを使用して音楽ファイルをロードします。librosa.load()関数を使用すると、オーディオファイルを解析し、2つのオブジェクトを返すことができます：

y（NumPy配列）：異なる時間区間の振幅値が含まれています。配列を表示してみてください！
sr（0より大きい数値）：サンプリングレート

サンプリングレートは、アナログ信号をデジタル表現に変換する際に、単位時間あたりに取得されるサンプル数を指します。上記で説明したように、VoAGI全体の圧力変動はアナログ信号を構成し、時間に連続的に変動する波形を持ちます。理論的には、連続データを格納するには無限の容量が必要です。したがって、これらのアナログ信号をデジタル的に処理および格納するためには、離散的な表現に変換する必要があります。これは、サンプリングが、離散（均等に間隔を空けて）時間間隔で音波のスクリーンショットをキャプチャする役割を果たすところです。これらの間隔の間隔は、サンプリングレートの逆数によって捉えられます。

サンプリングレートは、アナログ信号からサンプルを取得する頻度を決定し、そのためにサンプル数（秒あたりまたはヘルツで測定される）を意味します。より高いサンプリングレートは、毎秒より多くのサンプルが取得されるため、元のアナログ信号のより正確な表現を提供しますが、より多くのメモリリソースが必要です。対照的に、より低いサンプリングレートは、毎秒より少ないサンプルが取得されるため、元のアナログ信号のより正確な表現を提供しますが、より少ないメモリリソースが必要です。

通常のデフォルトのサンプリングレートは22050です。ただし、アプリケーション/メモリに応じて、ユーザーはより低いまたは高いサンプリングレートを選択することができます。これはlibrosa.load()のsr引数で指定することができます。アナログからデジタルへの変換に適切なサンプリングレートを選択する際には、ナイキスト・シャノンのサンプリング定理について知ることが重要かもしれません。この定理によれば、アナログ信号を正確にキャプチャして再構築するためには、サンプリングレートはオーディオ信号に存在する最高周波数成分の2倍以上でなければなりません（ナイキストレート/周波数と呼ばれます）。

ナイキスト周波数よりも高い周波数でサンプリングすることで、エイリアシングと呼ばれる現象を回避することができます。本記事の目的にはエイリアシングについての議論は特に関係ありませんが、興味がある場合は、以下の優れたソースを参照してください：https://thewolfsound.com/what-is-aliasing-what-causes-it-how-to-avoid-it/

次に、オーディオ信号を読み込むためのコードを示します：

# 音楽をlibrosaでロードする
sr = 22050
acoustic_guitar, sr = librosa.load(acoustic_guitar_path, sr=sr)
brass, sr = librosa.load(brass_path, sr=sr)
drum_set, sr = librosa.load(drum_set_path, sr=sr)

上記の例では、サンプリングレートは22050（デフォルトのレートでもあります）と言われています。上記のコードを実行すると、3つの配列が返されます。それぞれの配列は、離散的な時間間隔（サンプリングレートによって指定される）での振幅値を格納しています。次に、librosa.display.waveshow()を使用して3つのオーディオサンプルの波形を視覚化します。振幅密度をより明確に可視化するために、いくらかの透明度が追加されています（alpha=0.5）。

def show_waveform(signal, name=""):
    # 特定の大きさの新しい図を作成します
    plt.figure(figsize=(15, 7))
    # librosaを使用して信号の波形を表示します
    librosa.display.waveshow(signal, alpha=0.5)
    # プロットのタイトルを設定します
    plt.title("Waveform for " + name)
    # プロットを表示します
    plt.show()
show_waveform(acoustic_guitar, "Acoustic Guitar")
show_waveform(brass, "Brass")
show_waveform(drum_set, "Drum Set")

上記のプロットをじっくり見てください。見えるパターンについて考えてみてください。アコースティックギターの波形では、振幅の定期的な振動によって特徴付けられる周期的なパターンが確認できます。これは、ギターの音の複雑な波形を生成する弾かれた弦による振動に対応しており、多くの倍音が特徴的な音色と音質に寄与しています。

同様に、ブラスの波形も周期的なパターンを示し、一貫した音高と音質を持っています。ブラス楽器は、楽器奏者の唇を吹き込むことによって音を生成します。この吹き込む動作によって、特徴的な倍音と振幅変動の規則的なパターンを持つ波形が生成されます。

対照的に、ドラムセットの波形は明確な周期的なパターンを示しません。ドラムはドラムスティックや手がドラムヘッドや他の打楽器の表面に衝撃を与えることで音を出すため、振幅や持続時間が異なる複雑で不規則な波形が生成されます。区別できる周期的なパターンの欠如は、ドラムの音の打楽器的で非音調的な性質を反映しています。

オーディオ信号処理の基礎：フレームサイズとホップ長

重要な時間領域オーディオ特徴について説明する前に、フレームサイズとホップ長という2つの重要な特徴抽出パラメータについて話しましょう。通常、信号がデジタル処理されると、フレームに分割されます（重なる場合もあれば、重ならない場合もあります）。フレームの長さは、これらのフレームのサイズを示し、ホップ長はフレームの重なり具合に関する情報を包括します。では、なぜフレーミングが重要なのでしょうか？

フレーミングの目的は、信号の異なる特徴の時間変動を捉えることです。通常の特徴抽出方法では、入力信号の1つの数字の要約（平均、最小値、最大値など）が得られます。これらの特徴抽出方法を直接使用する問題は、これにより時間に関連する情報が完全に失われることです。たとえば、信号の平均振幅を計算する場合、単一の数値の要約（xと仮定します）が得られます。しかし、自然な場合では、平均が低い間隔と高い間隔が存在します。単一の数値の要約を取ると、平均の時間変動に関する情報が失われます。そのため、信号をフレームに分割することが解決策です。たとえば、[0 ms、10 ms）、[10 ms、20 ms）…といった時間フレームごとに信号の一部の平均が計算され、この集合的な特徴セットが最終的な抽出特徴ベクトル、つまり時間依存の特徴の要約を与えます。これは素晴らしいですね！

さて、詳細に2つのパラメータについて話しましょう：

フレームサイズ：各フレームのサイズを示します。たとえば、フレームサイズが1024の場合、1024サンプルを各フレームに含め、これらの1024サンプルのセットごとに必要な特徴を計算します。一般的には、フレームサイズを2のべき乗とすることが推奨されています。その理由は、フーリエ変換（時間領域から周波数領域に信号を変換する非常に効率的なアルゴリズム）にフレームが2のべき乗のサイズであることが必要なためです。後のセクションでフーリエ変換についてさらに詳しく話します。
ホップ長：フレームがデータのシーケンス全体を横断する際のフレームの進行に関するサンプルの数を指します。フレームは、ホップ長で定義されたステップで信号内を移動するスライディングウィンドウのようなものと考えると役立ちます。各ステップでは、ウィンドウが信号またはシーケンスの新しいセクションに適用され、そのセグメントで特徴抽出が行われます。したがって、ホップ長は連続するオーディオフレーム間の重なりを決定します。フレームサイズと等しいホップ長は、フレームが前のフレームが終わる場所とまったく同じ場所から始まるため、重なりがないことを意味します。ただし、スペクトルリーク（信号を時間領域から周波数領域に変換する際に発生する現象）の影響を軽減するために、ウィンドウ関数が適用され、各フレームの端のデータが失われます（詳しい技術的な説明は本記事の目的を超えますが、気になる方はこちらのリンクをご覧ください：https://dspillustrations.com/pages/posts/misc/spectral-leakage-zero-padding-and-frequency-resolution.html）。したがって、フレーム間の重なりの程度が異なるように、中間的なホップ長が選ばれることがよくあります。

一般的に、ホップ長が小さいほど、信号の詳細や急激な変化をより高い時間分解能で捉えることができます。ただし、メモリの要件も増加します。逆に、ホップ長が大きいと、時間分解能は低下しますが、スペースの複雑さも低減されます。

注：上記の画像では、視覚化をより明確にするために、フレームサイズが非常に大きく表示されています。実際の目的では、選択されたフレームサイズははるかに小さいです（おそらく数千のサンプル、約20〜40ミリ秒）。

時間領域での異なる特徴抽出手法に進む前に、数学的な表記を明確にしておきましょう。この記事全体で以下の表記を使用します：

xᵢ: 第iサンプルの振幅
K: フレームサイズ

H: ホップ

上記のコードでは、amplitude_envelopeという関数を定義しています。この関数は、入力信号配列（librosa.load()を使用して生成されたもの）、フレームサイズ（K）、ホップ長（H）を引数として受け取り、フレーム数と同じサイズの配列を返します。配列のk番目の値は、k番目のフレームの振幅エンベロープの値に対応します。計算は、ホップ長によって決まるステップで、信号全体を走査する単純なforループを使用して行われます。これらの値を格納するためにリスト（res）が定義され、最終的に返す前にNumPy配列に変換されます。また、plot_amplitude_envelopeという別の関数も定義されており、同じセットの入力（name引数も含む）を受け取り、元のフレームに対して振幅エンベロープのプロットを重ねて表示します。波形をプロットするためには、前のセクションで説明したように、伝統的なlibrosa.display.waveform()が使用されています。

振幅エンベロープをプロットするためには、時間と対応する振幅エンベロープの値が必要です。時間の値は、非常に便利な関数であるlibrosa.frames_to_times()を使用して取得されます。この関数は、フレーム数に対応するイテラブル（range関数を使用して定義される）とホップ長の2つの入力を受け取り、各フレームの平均時間を生成します。その後、matplotlib.pyplotを使用して赤いプロットを重ねます。上記の手順は、時間領域の特徴抽出手法すべてに対して一貫して使用されます。

以下の図は、各楽器の計算された振幅エンベロープを示しています。これらは元の波形に赤い線として追加され、波形の上限を近似する傾向があります。振幅エンベロープは周期的なパターンだけでなく、金管楽器とアコースティックギター、ドラムセットとの音の振幅の一般的な差を示す低い強度も保存します。

Acoustic Guitarの振幅エンベロープ[Image by Author]

特徴2：ルート平均二乗エネルギー

次に、時間領域解析におけるもう一つの重要な特徴であるルート平均二乗エネルギー（RMSE）について説明します。オーディオ信号のフレームのルート平均二乗エネルギーは、フレーム内のすべての振幅値の二乗の平均値の平方根を取ることによって得られます。数学的には、k番目のフレームのルート平均二乗エネルギー（重なりのないフレームの場合）は次のように表されます：

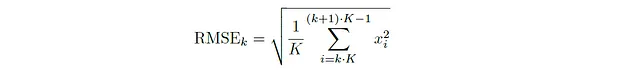
一般に、サンプルxⱼ₁、xⱼ₂、· · ·、xⱼₖを含むフレームkの場合、RMSEは次のようになります：

RMSエネルギーは、波形の正のおよび負の変動を両方考慮して、ピーク振幅などの他の測定値と比較して信号のパワーをより正確に測定するため、音信号の全体的な強度や強さを表現します。与えられた信号のRMSEを計算するためのPythonコードは以下の通りです。コードの構造は、振幅エンベロープを生成するためのものと同じです。唯一の違いは、特徴を抽出するために使用される関数です。最大値の代わりに、現在の信号の部分の二乗値の平均値を計算し、その後に平方根を取ることによってRMSE値が計算されます。

def RMS_energy(signal, frame_size=1024, hop_length=512):    """    スライディングウィンドウを使用して信号のRMS（ルート平均二乗）エネルギーを計算します。    Args:        signal (array): 入力信号。        frame_size (int): サンプルごとのフレームサイズ。        hop_length (int): 連続するフレーム間のサンプル数。    Returns:        np.array: RMSエネルギー値の配列。    """    res = []    for i in range(0, len(signal), hop_length):        # 信号の一部を抽出        cur_portion = signal[i:i + frame_size]          # その部分のRMSエネルギーを計算        rmse_val = np.sqrt(1 / len(cur_portion) * sum(i**2 for i in cur_portion))          res.append(rmse_val)    # 結果をNumPy配列に変換    return np.array(res)def plot_RMS_energy(signal, name, frame_size=1024, hop_length=512):    """    RMSエネルギー値をオーバーレイした信号の波形をプロットします。    Args:        signal (array): 入力信号。        name (str): プロットのタイトルに使用する信号の名前。        frame_size (int): サンプルごとのフレームサイズ。        hop_length (int): 連続するフレーム間のサンプル数。    """    # RMSエネルギーの計算    rmse = RMS_energy(signal, frame_size, hop_length)    # フレームのインデックスを生成    frames = range(0, len(rmse))      # フレームを時間に変換    time = librosa.frames_to_time(frames, hop_length=hop_length)     # 特定のサイズの新しい図を作成    plt.figure(figsize=(15, 7))    # スペクトログラムのようなプロットとして波形を表示    librosa.display.waveshow(signal, alpha=0.5)      # RMSエネルギー値をプロット    plt.plot(time, rmse, color="r")     # プロットのタイトルを設定    plt.title(name + "の波形（RMSエネルギー）")    plt.show()plot_RMS_energy(acoustic_guitar, "Acoustic Guitar")plot_RMS_energy(brass, "Brass")plot_RMS_energy(drum_set, "Drum Set")

次の図は、各楽器の計算されたRMSエネルギーを示しています。これらは元の波形の上に赤い線として追加され、波形の重心を近似する傾向があります。前と同様に、この指標は周期的なパターンだけでなく、音波の全体的な強度レベルも近似します。

特徴3：クレストファクター

次に、波形のピークの極端さを測るクレストファクターについて話しましょう。オーディオ信号のフレームのクレストファクターは、ピーク振幅（振幅の最大絶対値）をRMSエネルギーで割ることによって得られます。数学的には、k番目のフレーム（オーバーラップしないフレームの場合）のクレストファクターは次のように与えられます：

一般的に、サンプルxⱼ₁、xⱼ₂、···、xⱼₖを含む任意のフレームkに対して、クレストファクターは次のようになります：

クレストファクターは、波形の最高ピークレベルと平均強度レベルの比率を示します。与えられた信号のクレストファクターを計算するためのPythonコードは以下の通りです。構造は上記と同様で、RMSE値（分母）と最高ピーク値（分子）の計算を含みます。これらを使用して目的の分数（クレストファクター！）を取得します。

def crest_factor(signal, frame_size=1024, hop_length=512):    """    スライディングウィンドウを使用して信号のクレストファクターを計算します。    Args:        signal (array): 入力信号。        frame_size (int): 各フレームのサンプル数。        hop_length (int): 連続するフレーム間のサンプル数。    Returns:        np.array: クレストファクターの値の配列。    """    res = []    for i in range(0, len(signal), hop_length):        # 信号の一部を取得        cur_portion = signal[i:i + frame_size]          # その部分のRMSエネルギーを計算        rmse_val = np.sqrt(1 / len(cur_portion) * sum(i ** 2 for i in cur_portion))          # クレストファクターを計算        crest_val = max(np.abs(cur_portion)) / rmse_val          # クレストファクターの値を保存        res.append(crest_val)      # 結果をNumPy配列に変換    return np.array(res)  def plot_crest_factor(signal, name, frame_size=1024, hop_length=512):    """    信号のクレストファクターを時間に沿ってプロットします。    Args:        signal (array): 入力信号。        name (str): プロットのタイトルに使用する信号の名前。        frame_size (int): 各フレームのサンプル数。        hop_length (int): 連続するフレーム間のサンプル数。    """    # クレストファクターを計算    crest = crest_factor(signal, frame_size, hop_length)      # フレームのインデックスを生成    frames = range(0, len(crest))      # フレームを時間に変換    time = librosa.frames_to_time(frames, hop_length=hop_length)      # 特定のサイズで新しい図を作成    plt.figure(figsize=(15, 7))      # 時間に沿ったクレストファクターをプロット    plt.plot(time, crest, color="r")      # プロットのタイトルを設定    plt.title(name + " (クレストファクター)")      # プロットを表示    plt.show()      plot_crest_factor(acoustic_guitar, "アコースティックギター")plot_crest_factor(brass, "ブラス")plot_crest_factor(drum_set, "ドラムセット")

以下の図は、各楽器の計算されたクレストファクターを示しています：

アコースティックギターやブラスのような高いクレストファクターは、ピークレベルと平均レベルの間の差が大きく、振幅の変動が大きい、よりダイナミックまたはピークのある信号を示しています。ドラムセットのような低いクレストファクターは、振幅の変動が小さく、より均一または圧縮された信号を示しています。クレストファクターは、システムのヘッドルームや利用可能なダイナミックレンジを考慮する必要がある場合に特に重要です。たとえば、音楽の録音で高いクレストファクターがある場合、限られたヘッドルームを持つ機器で再生する際に歪みやクリッピングを防ぐために注意が必要です。

実際には、クレストファクターに密接に関連するピーク-平均電力比（PAPR）と呼ばれる別の特徴があります。PAPRはクレストファクターの2乗値であり、通常はデシベル電力比に変換されます。一般的に、サンプルxⱼ₁、xⱼ₂、· · ·、xⱼₖを含む任意のフレームkの場合、ピーク-平均電力比は次のようになります：

楽しいチャレンジとして、上記のコードを変更して3つの楽器のPAPRのプロットを生成し、結果を分析してみてください。

特徴4：ゼロクロスレート

最後に、ゼロクロスレート（ZCR）について説明します。オーディオ信号のフレームのゼロクロスレートは、単純に信号がゼロ（x/時間軸）を横切る回数です。数学的には、k番目のフレームのZCR（オーバーラップしないフレームの場合）は次のようになります：

連続する値が同じ符号を持つ場合、絶対値内の式はキャンセルされ、0が得られます。互いに逆の符号を持つ場合（信号が時間軸を横切ったことを示す）、値が追加され、絶対値を取った後に2になります。ゼロクロスは値2を与えるため、結果に必要なカウントを得るために結果に半分の係数を乗算します。一般的に、サンプルxⱼ₁、xⱼ₂、· · ·、xⱼₖを含む任意のフレームkの場合、ZCRは次のようになります：

上記の式では、ゼロクロスレートは信号が軸を横切る回数を単純に合計して計算されます。ただし、応用によっては値を正規化することもできます（フレームの長さで割るなど）。与えられた信号のクレストファクターを計算するためのPythonコードは以下の通りです。構造は上記からの続きで、与えられた信号の符号がいくつ変化するかを決定するnum sign changesという別の関数の定義が含まれます。

def ZCR(signal, frame_size=1024, hop_length=512):    """    スライディングウィンドウを使用して信号のゼロクロスレート（ZCR）を計算します。    Args:        signal (array): 入力信号。        frame_size (int): サンプルごとの各フレームのサイズ。        hop_length (int): 連続するフレーム間のサンプル数。    Returns:        np.array: ZCRの値の配列。    """    res = []    for i in range(0, len(signal), hop_length):        # 信号の一部を取得        cur_portion = signal[i:i + frame_size]           # 一部の信号内の符号変化の数を計算        zcr_val = num_sign_changes(cur_portion)         # ZCRの値を保存        res.append(zcr_val)      # 結果をNumPy配列に変換    return np.array(res)  def num_sign_changes(signal):    """    信号内の符号変化の数を計算します。    Args:        signal (array): 入力信号。    Returns:        int: 符号変化の数。    """    res = 0    for i in range(0, len(signal) - 1):        # 連続するサンプル間で符号の変化があるかをチェック        if (signal[i] * signal[i + 1] < 0):              res += 1    return resdef plot_ZCR(signal, name, frame_size=1024, hop_length=512):    """    信号のゼロクロスレート（ZCR）を時間の経過に沿ってプロットします。    Args:        signal (array): 入力信号。        name (str): プロットのタイトルの信号の名前。        frame_size (int): サンプルごとの各フレームのサイズ。        hop_length (int): 連続するフレーム間のサンプル数。    """    # ZCRを計算    zcr = ZCR(signal, frame_size, hop_length)      # フレームのインデックスを生成    frames = range(0, len(zcr))     # フレームを時間に変換    time = librosa.frames_to_time(frames, hop_length=hop_length)       # 特定のサイズで新しい図を作成    plt.figure(figsize=(15, 7))     # 時間の経過に沿ってZCRをプロット    plt.plot(time, zcr, color="r")      # プロットのタイトルを設定    plt.title(name + "（ゼロクロスレート）")      # プロットを表示    plt.show()      plot_ZCR(acoustic_guitar, "アコースティックギター")plot_ZCR(brass, "ブラス")plot_ZCR(drum_set, "ドラムセット")

以下の図は、各楽器の計算されたゼロ交差率を示しています。

ゼロ交差率が高いほど、信号が頻繁に方向を変えることを示し、高周波成分やより動的な波形の存在を示唆します。逆に、ゼロ交差率が低いと比較的滑らかなまたは一定の波形を示します。

ゼロ交差率は、音声や音楽の分析の応用において特に有用であり、音色やリズムパターンなどの特性に関する洞察を提供する能力を持っています。たとえば、音声分析では、ゼロ交差率は声帯の振動によるということから、声帯音と非声帯音を区別するのに役立ちます。ゼロ交差率は、シンプルかつ計算効率が良い特徴量ですが、信号の複雑さのすべての側面を捉えることができない場合があります（上記の図では周期性が完全に失われていることがわかります）。そのため、より包括的なオーディオ信号の分析のために他の特徴量と組み合わせて使用されることがよくあります。

周波数領域の特徴抽出

周波数領域は、オーディオ波形の別の表現方法を提供します。時間領域では、信号は時間の関数として表されますが、周波数領域では、信号は構成する周波数ごとに分解され、各周波数に関連する振幅と位相情報が明らかになります。つまり、信号は周波数の関数として表されます。時間のさまざまな時点での信号の振幅ではなく、信号を構成する異なる周波数成分の振幅を調べることになります。それぞれの周波数成分は特定の周波数の正弦波を表し、これらの成分を組み合わせることで、元の信号を時間領域で再構成することができます。

（最も一般的な）数学的なツールであるフーリエ変換は、信号を時間領域から周波数領域に変換するために使用されます。フーリエ変換は、信号を入力として受け取り、振幅と位相を持つさまざまな周波数の正弦波と余弦波の和に分解します。これにより得られる表現が周波数スペクトルです。数学的には、連続信号の時間領域g(t)のフーリエ変換は次のように定義されます：

i = √−1は虚数です。フーリエ変換は、位相と振幅がそれぞれの成分の正弦波と一致するため、複素数の出力を生成します。ただし、ほとんどのアプリケーションでは、変換の振幅のみに関心があり、関連する位相は無視されます。デジタルで処理される音は離散的であるため、同様の離散フーリエ変換（DFT）を定義することができます：

Tは1つのサンプルの時間です。サンプリングレートに関しては、次のように表されます：

周波数表現も連続的であるため、離散化された周波数ビン上でフーリエ変換を評価し、オーディオ波形の離散周波数領域表現を得ることができます。これは短時間フーリエ変換と呼ばれます。数学的には、次のように表されます：

心配しないでください！ゆっくりと復習しましょう。ハット関数 h(k) は、整数 k ∈ {0, 1, · · · , N − 1} を周波数 k · Sᵣ/N の大きさに対応させる関数です。ここで、信号内のサンプル数を表す N に対して、Sᵣ/N の整数倍の離散周波数ビンのみを考慮しています。これがどのように機能するかについてまだ不明な場合は、以下の優れたフーリエ変換の説明をご覧ください: https://www.youtube.com/watch?v=spUNpyF58BY&t=393s

フーリエ変換は、最も美しい数学の革新の一つであり、この記事の目的とは直接関係がないにもかかわらず、それを知る価値があります。Pythonでは、librosa.stft()を使用して簡単に短時間フーリエ変換を取得できます。

注意: 音声データの場合、より効率的なフーリエ変換の計算方法である高速フーリエ変換（FFT）がありますので、興味があればぜひチェックしてみてください！

以前と同様に、どの周波数がより優勢であるかを知るだけでなく、これらの周波数が優勢である時点も表示したいと考えています。そのために、フレーム分割が登場します：信号を時間フレームに分割し、各フレームで得られたフーリエ変換の大きさを取得します。これにより、行数が周波数ビンの数（Φ、通常はフレームサイズ K/2 + 1）で与えられ、列数がフレーム数で与えられる値の行列が得られます。フーリエ変換は複素値の出力を与えるため、生成される行列も複素値です。Pythonでは、フレームサイズとホップ長のパラメーターを引数として指定し、結果の行列を簡単に計算することができます。ただし、大きさのみに関心があるため、複素値の行列を実数値の行列に変換するために numpy.abs() を使用することができます。与えられた音の周波数内容と時間特性に関する貴重な洞察を提供する視覚的に魅力的な信号の表現を得るために、この行列をプロットすることは非常に便利です。このような表現はスペクトログラムと呼ばれます。

スペクトログラムは、x軸に時間フレーム、y軸に周波数ビンをプロットして得られます。色は、指定された時間フレームの周波数の強度または大きさを示すために使用されます。通常、周波数軸は対数スケールに変換されます（人間は対数変換下でより良く認識できるとされているため）、大きさはデシベルで表されます。

スペクトログラムを生成するためのPythonコードは以下の通りです:

FRAME_SIZE = 1024HOP_LENGTH = 512def plot_spectrogram(signal, sample_rate, frame_size=1024, hop_length=512):    """    オーディオ信号のスペクトログラムをプロットします。    Args:        signal (array-like): 入力オーディオ信号。        sample_rate (int): オーディオ信号のサンプリングレート。        frame_size (int): 各フレームのサンプル数。        hop_length (int): 連続するフレーム間のサンプル数。    """    # STFTを計算する    spectrogram = librosa.stft(signal, n_fft=frame_size, hop_length=hop_length)      # STFTをdBスケールに変換する    spectrogram_db = librosa.amplitude_to_db(np.abs(spectrogram))      # 特定のサイズの新しい図を作成する    plt.figure(figsize=(15, 7))      # スペクトログラムを表示する    librosa.display.specshow(spectrogram_db, sr=sample_rate, hop_length=hop_length, x_axis='time', y_axis='log')     # 大きさのスケールを表示するためにカラーバーを追加する    plt.colorbar(format='%+2.0f dB')     # プロットのタイトルを設定する    plt.title('スペクトログラム')      # x軸のラベルを設定する    plt.xlabel('時間')     # y軸のラベルを設定する    plt.ylabel('周波数 (Hz)')      # プロットのレイアウトを調整する    plt.tight_layout()      # プロットを表示する    plt.show()      plot_spectrogram(acoustic_guitar, sr)plot_spectrogram(brass, sr)plot_spectrogram(drum_set, sr)

上記のコードでは、plot_spectrogramという名前の関数を定義しています。この関数は、入力信号配列、サンプリングレート、フレームサイズ、ホップ長の4つの引数を受け取ります。まず、librosa.stft()を使用してスペクトログラム行列を取得します。その後、np.abs()を使用して大きさを抽出し、関数librosa.amplitude_to_db()を使用して振幅値をデシベルに変換します。最後に、関数librosa.display.specshow()を使用してスペクトログラムをプロットします。この関数は、変換されたスペクトログラム行列、サンプリングレート、ホップ長、およびx軸とy軸の仕様を受け取ります。対数変換されたy軸は、y_axis=’log’の引数を使用して指定できます。オプションのカラーバーはplt.colorbar()を使用して追加できます。3つの楽器のスペクトログラムは以下に示されています:

スペクトログラムは、時間と周波数のトレードオフを視覚化するユニークな方法を提供します。時間領域は、信号が時間の経過に伴ってどのように変化するかを正確に表現します。一方、周波数領域は、異なる周波数のエネルギーの分布を見ることができます。これにより、特定の周波数の存在だけでなく、その持続時間や時間的な変動も把握することができます。スペクトログラムは音を表現するための最も有用な手法の一つであり、オーディオ信号の機械学習アプリケーション（例えば、サウンドウェーブのスペクトログラムをディープコンボリューションニューラルネットワークに入力して予測する）で頻繁に使用されます。

異なる周波数領域の特徴抽出手法に進む前に、数学的な表記法を明確にしておきましょう。次の表記法を後続のセクションで使用します：

mₖ(i)：k番目のフレームのi番目の周波数の振幅。
K：フレームサイズ
H：ホップ長
Φ：周波数ビンの数（= K/2 + 1）

特徴5：バンドエネルギー比

まず、バンドエネルギー比について話しましょう。バンドエネルギー比は、与えられた時間フレーム内で低周波数のエネルギーと高周波数のエネルギーの比を量化するための指標です。数学的には、任意のフレームkに対して、バンドエネルギー比は次のようになります：

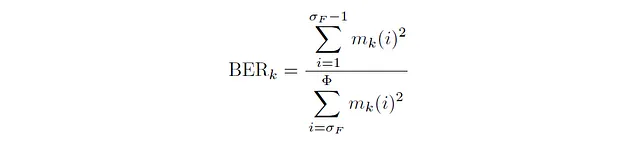
ここで、σբは分割周波数ビンを示し、低周波数と高周波数を区別するためのパラメータです。バンドエネルギー比を計算する際には、σբに対応する周波数よりも値が小さいすべての周波数が低周波数とみなされます。これらの周波数の二乗エネルギーの合計が分子となります。同様に、σբよりも値が大きいすべての周波数が高周波数とみなされ、これらの周波数の二乗エネルギーの合計が分母となります。信号のバンドエネルギー比を計算するためのPythonコードは以下のとおりです：

def find_split_freq_bin(spec, split_freq, sample_rate, frame_size=1024, hop_length=512): """ 与えられた分割周波数に対応するビンインデックスを計算する。 Args: spec (array): スペクトログラム。 split_freq (float): 分割周波数（Hz）。 sample_rate (int): オーディオのサンプルレート。 frame_size (int, optional): 各フレームのサンプル数。デフォルトは1024です。 hop_length (int, optional): 連続するフレーム間のサンプル数。デフォルトは512です。 Returns: int: 分割周波数に対応するビンインデックス。 """ # 周波数の範囲を計算する range_of_freq = sample_rate / 2 # ビンごとの周波数の変化を計算する change_per_bin = range_of_freq / spec.shape[0] # 分割周波数に対応するビンを計算する split_freq_bin = split_freq / change_per_bin return int(np.floor(split_freq_bin))def band_energy_ratio(signal, split_freq, sample_rate, frame_size=1024, hop_length=512): """ 信号のバンドエネルギー比（BER）を計算する。 Args: signal (array): 入力信号。 split_freq (float): 分割周波数（Hz）。 sample_rate (int): オーディオのサンプルレート。 frame_size (int, optional): 各フレームのサンプル数。デフォルトは1024です。 hop_length (int, optional): 連続するフレーム間のサンプル数。デフォルトは512です。 Returns: ndarray: 信号の各フレームのバンドエネルギー比。 """ # 信号のスペクトログラムを計算する spec = librosa.stft(signal, n_fft=frame_size, hop_length=hop_length) # 分割周波数に対応するビンを見つける split_freq_bin = find_split_freq_bin(spec, split_freq, sample_rate, frame_size, hop_length) # 振幅を抽出して転置する modified_spec = np.abs(spec).T res = [] for sub_arr in modified_spec: # 低周波数範囲のエネルギーを計算する low_freq_density = sum(i ** 2 for i in sub_arr[:split_freq_bin]) # 高周波数範囲のエネルギーを計算する high_freq_density = sum(i ** 2 for i in sub_arr[split_freq_bin:]) # バンドエネルギー比を計算する ber_val = low_freq_density / high_freq_density res.append(ber_val) return np.array(res)def plot_band_energy_ratio(signal, split_freq, sample_rate, name, frame_size=1024, hop_length=512): """ 信号のバンドエネルギー比（BER）を時間の経過に沿ってプロットする。 Args: signal (ndarray): 入力信号。 split_freq (float): 分割周波数（Hz）。 sample_rate (int): オーディオのサンプルレート。 name (str): プロットのタイトルとなる信号の名前。 frame_size (int, optional): 各フレームのサンプル数。デフォルトは1024です。 hop_length (int, optional): 連続するフレーム間のサンプル数。デフォルトは512です。 """ # バンドエネルギー比（BER）を計算する ber = band_energy_ratio(signal, split_freq, sample_rate, frame_size, hop_length) # フレームインデックスを生成する frames = range(0, len(ber)) # フレームを時間に変換する time = librosa.frames_to_time(frames, hop_length=hop_length) # 特定のサイズで新しい図を作成する plt.figure(figsize=(15, 7)) # 時間の経過に沿ってBERをプロットする plt.plot(time, ber) # プロットのタイトルを設定する plt.title(name + " (バンドエネルギー比)") # プロットを表示する plt.show() plot_band_energy_ratio(acoustic_guitar, 2048, sr, "アコースティックギター")plot_band_energy_ratio(brass, 2048, sr, "ブラス")plot_band_energy_ratio(drum_set, 2048, sr, "ドラムセット")</pre

上記のコードの構造は、時間領域の抽出と非常に似ています。最初のステップは、spectrogram、分割周波数の値、およびサンプルレートを受け取り、分割周波数に対応する分割周波数ビン (σբ ) を決定するためのfind split_freq_bin()という関数を定義することです。このプロセスは非常にシンプルです。周波数の範囲（前述のようにナイキスト周波数、Sᵣ/2）を見つけることを含みます。周波数ビンの数は、spectrogramの行数によって与えられます。これはspec.shape[0]として抽出されます。周波数の総範囲を周波数ビンの数で割ることで、ビンごとの周波数の変化を計算し、与えられた分割周波数で割ることで、分割周波数ビンを決定することができます。

次に、この関数を使用してバンドエネルギー比ベクトルを計算します。band_energy_ratio()という関数は、入力信号、分割周波数、サンプルレート、フレームサイズ、およびホップ長を受け取ります。まず、librosa.stft()を使用してspectrogramを抽出し、次に分割周波数ビンを計算します。次に、np.abs()を使用してspectrogramの振幅を計算し、反転して各フレームを繰り返し処理するために準備します。繰り返し処理中に、定義された式と見つかった分割周波数ビンを使用して、各フレームのバンドエネルギー比を計算します。値はリストresに格納され、最終的にNumPy Arrayとして返されます。最後に、plot_band_energy_ratio()関数を使用して値をプロットします。

以下に3つの楽器のバンドエネルギー比プロットが示されています。これらのプロットでは、分割周波数を2048 Hzに設定しています。つまり、2048 Hz以下の周波数は低エネルギー周波数と見なされ、2048 Hz以上の周波数は高エネルギー周波数と見なされます。

Band Energy Ratio for Acoustic Guitar [Image by Author] — アコースティックギターのバンドエネルギー比[Image by Author]

Band Energy Ratio for Brass [Image by Author] — ブラスのバンドエネルギー比[Image by Author]

Band Energy Ratio for Drum Set [Image by Author] — ドラムセットのバンドエネルギー比[Image by Author]

ブラスの高いバンドエネルギー比は、高周波成分に対して低周波成分の存在がより大きいことを示しています。したがって、ブラス楽器は、他の楽器に比べて低周波帯において相当量のエネルギーを生成します。アコースティックギターは、ブラス楽器と比較して低いBERを持っており、低周波帯におけるエネルギーの寄与が比較的少ないことを示しています。一般的に、アコースティックギターは、他の楽器と比較して周波数スペクトル全体におけるエネルギー分布がよりバランスされており、低周波数に対する重点が相対的に少ない傾向があります。最後に、ドラムセットは3つの楽器の中で最も低いBERを持っており、他の楽器に比べて低周波帯におけるエネルギー寄与が比較的少ないことを示しています。

特徴6：スペクトル重心

次に、スペクトル重心について説明します。スペクトル重心は、信号のスペクトルの中心または平均周波数を特定の時間枠で定量化する指標です。数学的には、任意のフレームkに対して、スペクトル重心は次のようになります：

これは、周波数ビンのインデックスの重み付き合計であり、重みは与えられた時間フレーム内のビンのエネルギー寄与によって決まります。正規化も行われ、重みの合計で重み付き合計を割ることで、異なる信号間での一様な比較を容易にします。信号のスペクトル重心を計算するためのPythonコードは以下のとおりです：

def spectral_centroid(signal, sample_rate, frame_size=1024, hop_length=512):    """    信号のスペクトル重心を計算します。    Args:        signal (array): 入力信号。        sample_rate (int): オーディオのサンプルレート。        frame_size (int, optional): 各フレームのサイズ（サンプル数）。デフォルトは1024です。        hop_length (int, optional): 連続するフレーム間のサンプル数。デフォルトは512です。    Returns:        ndarray: 信号の各フレームのスペクトル重心。    """    # 信号のスペクトログラムを計算する    spec = librosa.stft(signal, n_fft=frame_size, hop_length=hop_length)    # 振幅を抽出して転置する    modified_spec = np.abs(spec).T    res = []    for sub_arr in modified_spec:        # スペクトル重心を計算する        sc_val = sc(sub_arr)        # 現在のフレームのスペクトル重心の値を格納する        res.append(sc_val)    return np.array(res)def sc(arr):    """    信号のスペクトル重心を計算します。    Args:        arr (array): 現在のフレームの周波数領域配列。    Returns:        float: 現在のフレームのスペクトル重心の値。    """    res = 0    for i in range(0, len(arr)):        # 重み付き合計を計算する        res += i*arr[i]    return res/sum(arr)def bin_to_freq(spec, bin_val,上記のコードでは、スペクトル重心関数が定義され、すべてのフレームのスペクトル重心の配列を生成するようになっています。その後、sc()関数が定義され、インデックス値を振幅と乗算し、正規化して平均周波数ビンを取得する単純な反復プロセスによって1つのフレームのスペクトル重心を計算します。spectral_centroid()が返すスペクトル重心値をプロットする前に、プロットのためのヘルパー関数としてbin to freqという別の関数が定義されます。この関数は、平均ビン値を対応する周波数値に変換し、スペクトログラム上にプロットすることで、時間にわたるスペクトル重心の変動の一貫したイメージを得るために使用されます。出力プロット（スペクトログラム上の重心変動のオーバーレイ付き）は以下に示されています：
アコースティックギターのスペクトル重心[Image by Author]
金管楽器のスペクトル重心[Image by Author]
ドラムセットのスペクトル重心[Image by Author]
スペクトル重心は、時間領域解析のRMSE指標に非常に類似しており、音の音色や明るさの記述子として一般的に使用されます。スペクトル重心が高い音は、より明るくまたは高音志向の特性を持ち、低い重心値はむしろ暗くまたは低音志向の特性と関連付けられます。スペクトル重心は、音楽ジャンル分類を含むオーディオ機械学習の最も重要な特徴の1つです。
特徴7：スペクトル帯域幅
さて、スペクトル帯域幅/拡散について話しましょう。これは、信号のスペクトルの成分周波数全体にわたるエネルギーの拡散を量子化する尺度です。スペクトル重心が平均値であるならば、スペクトル帯域幅はその重心に対する拡散/分散の尺度です。数学的には、任意のフレームkに対して、スペクトル帯域幅は次のようになります：
ここで、SCₖはk番目のフレームのスペクトル重心を表します。先ほどと同様に、正規化は重みの総和で重み付きの合計を除算することで行われ、異なる信号間での一様な比較を容易にします。信号のスペクトル帯域幅を計算するためのPythonコードは以下の通りです：
def spectral_bandwidth(signal, sample_rate, frame_size=1024, hop_length=512):    """    シグナルのスペクトル帯域幅を計算します。    Args:        signal (array): 入力シグナル。        sample_rate (int): オーディオのサンプルレート。        frame_size (int, optional): 各フレームのサイズ（サンプル数）。デフォルトは1024です。        hop_length (int, optional): 連続するフレーム間のサンプル数。デフォルトは512です。    Returns:        ndarray: シグナルの各フレームのスペクトル帯域幅。    """    # シグナルのスペクトログラムを計算する    spec = librosa.stft(signal, n_fft=frame_size, hop_length=hop_length)    # 振幅を抽出して転置する    modified_spec = np.abs(spec).T    res = []    for sub_arr in modified_spec:        # スペクトル帯域幅を計算する        sb_val = sb(sub_arr)        # 現在のフレームのスペクトル帯域幅の値を格納する        res.append(sb_val)    return np.array(res)def sb(arr):    """    シグナルのスペクトル帯域幅を計算します。    Args:        arr (array): 現在のフレームの周波数ドメイン配列。    Returns:        float: 現在のフレームのスペクトル帯域幅の値。    """    res = 0    sc_val = sc(arr)    for i in range(0, len(arr)):        # 重み付き合計を計算する        res += (abs(i - sc_val))*arr[i]    return res/sum(arr)def plot_spectral_bandwidth(signal, sample_rate, name, frame_size=1024, hop_length=512):    """    シグナルのスペクトル帯域幅を時間とともにプロットします。    Args:        signal (ndarray): 入力シグナル。        sample_rate (int): オーディオのサンプルレート。        name (str): プロットのタイトルに使用されるシグナルの名前。        frame_size (int, optional): 各フレームのサイズ（サンプル数）。デフォルトは1024です。        hop_length (int, optional): 連続するフレーム間のサンプル数。デフォルトは512です。    """    # スペクトル帯域幅を計算する    sb_arr = spectral_bandwidth(signal, sample_rate, frame_size, hop_length)    # フレームのインデックスを生成する    frames = range(0, len(sb_arr))    # フレームを時間に変換する    time = librosa.frames_to_time(frames, hop_length=hop_length)    # 特定のサイズの新しい図を作成する    plt.figure(figsize=(15, 7))    # 時間とともにスペクトル帯域幅をプロットする    plt.plot(time, sb_arr)    # プロットのタイトルを設定する    plt.title(name + " (スペクトル帯域幅)")    # プロットを表示する    plt.show()    plot_spectral_bandwidth(acoustic_guitar, sr, "アコースティックギター")plot_spectral_bandwidth(brass, sr, "金管楽器")plot_spectral_bandwidth(drum_set, sr, "ドラムセット")
上記のコードと同様に、上記のコードでは、spectral bandwidth関数がsbヘルパー関数を使用して、1つのフレームの帯域幅を反復的に計算し、すべての時間フレームのスペクトルスプレッドの配列を生成するように定義されています。最後に、plot spectral bandwidth関数を使用して、これらの帯域幅の値をプロットします。出力プロットは以下に表示されます：
アコースティックギターアコースティックギターのスペクトル帯域幅 [Image by Author]
ブラスのスペクトル帯域幅 [Image by Author]
ドラムセットのスペクトル帯域幅 [Image by Author]
スペクトル帯域幅は、信号中の周波数の広がりや幅に関する情報を提供する能力を持つため、さまざまなオーディオ分析/分類のタスクで使用することができます。より高いスペクトル帯域幅（ブラスとドラムセットで見られるように）は、より広い範囲の周波数を示し、より多様または複雑な信号を示唆しています。一方、より低い帯域幅は、より狭い周波数範囲を示し、より焦点を絞ったまたは音的に純粋な信号を示します。
特徴8：スペクトル平坦度
最後に、スペクトル平坦度（またはウィーナエントロピー）について説明します。これは、オーディオ信号のパワースペクトルの平坦性または均一性に関する情報を提供する尺度です。オーディオ信号が純音にどれだけ近いか（ノイズのようなものではないか）を知るのに役立ち、そのために音調係数とも呼ばれています。任意のフレームkに対して、スペクトル平坦度はその幾何平均を算術平均で割った比率です。数学的には、

信号のスペクトル平坦度を計算するためのPythonコードは以下の通りです：
def spectral_flatness(signal, sample_rate, frame_size=1024, hop_length=512):    """    シグナルのスペクトル平坦度を計算します。    Args:        signal (array): 入力信号。        sample_rate (int): オーディオのサンプルレート。        frame_size (int, optional): フレームのサイズ（サンプル数）。デフォルトは1024です。        hop_length (int, optional): 連続するフレーム間のサンプル数。デフォルトは512です。    Returns:        ndarray: シグナルの各フレームのスペクトル平坦度。    """    # シグナルのスペクトログラムを計算する    spec = librosa.stft(signal, n_fft=frame_size, hop_length=hop_length)    # magnitudeを抽出して転置する    modified_spec = np.abs(spec).T    res = []    for sub_arr in modified_spec:        # 幾何平均を計算する        geom_mean = np.exp(np.log(sub_arr).mean())        # 算術平均を計算する        ar_mean = np.mean(sub_arr)        # スペクトル平坦度を計算する        sl_val = geom_mean/ar_mean        # 現在のフレームのスペクトル平坦度の値を保存する        res.append(sl_val)    return np.array(res)def plot_spectral_flatness(signal, sample_rate, name, frame_size=1024, hop_length=512):    """    シグナルのスペクトル平坦度を時間に沿ってプロットします。    Args:        signal (ndarray): 入力信号。        sample_rate (int): オーディオのサンプルレート。        name (str): プロットのタイトルに使用する信号の名前。        frame_size (int, optional): フレームのサイズ（サンプル数）。デフォルトは1024です。        hop_length (int, optional): 連続するフレーム間のサンプル数。デフォルトは512です。    """    # スペクトル平坦度を計算する    sl_arr = spectral_flatness(signal, sample_rate, frame_size, hop_length)    # フレームのインデックスを生成する    frames = range(0, len(sl_arr))    # フレームを時間に変換する    time = librosa.frames_to_time(frames, hop_length=hop_length)    # 特定のサイズの新しい図を作成する    plt.figure(figsize=(15, 7))    # 時間に沿ってスペクトル平坦度をプロットする    plt.plot(time, sl_arr)    # プロットのタイトルを設定する    plt.title(name + " (スペクトル平坦度)")    # プロットを表示する    plt.show()    plot_spectral_flatness(acoustic_guitar, sr, "アコースティックギター")plot_spectral_flatness(brass, sr, "ブラス")plot_spectral_flatness(drum_set, sr, "ドラムセット")
上記のコードの構造は、他の周波数領域抽出方法と同じです。唯一の違いは、forループ内の特徴抽出関数にあります。この関数はNumPy関数を使用して算術平均と幾何平均を計算し、それらの比率を計算して各時間フレームのスペクトル平坦度の値を生成します。出力プロットは以下の通りです：
アコースティックギターのスペクトル平坦度 [Image by Author]
ブラスのスペクトル平坦度 [Image by Author]
ドラムセットのスペクトル平坦度 [Image by Author]
スペクトル平坦度が高い値（1に近い値）は、信号の異なる周波数間でのエネルギーの一様またはバランスの取れた分布を示します。これは、ドラムセットでは一貫して見られ、より「ノイズのような」または広帯域であり、特定の周波数に顕著なピークや強調がない音を示唆しています（周期性の欠如から既に気づかれています）。
一方で、スペクトル平坦度の低い値（特にアコースティックギターや一部のブラスに対して）は、エネルギーが特定の周波数周辺に集中しているより均等でないパワースペクトルを示します。これは、音の音調や調和成分の存在を示しています（周期的な時間領域の構造に反映されています）。一般的に、明確な音高/周波数を持つ音楽は、スペクトル平坦度が低くなりますが、ノイズ（非音調）のある音は、スペクトル平坦度が高くなります。
結論
この記事では、音響工学のオーディオ信号処理の重要な要素である特徴抽出の異なる戦略と技術について詳しく説明しました。音の生成と伝播の基礎から学び、時間領域表現における時間による圧力変動に効果的に変換されることができることを始めに学びました。サンプリングレート、フレームサイズ、ホップ長を含む、音のデジタル表現とその重要なパラメータについて議論しました。振幅包絡線、二乗平均平方根エネルギー、クレストファクター、ピークパワー比、ゼロクロス数などの時間領域特徴について理論的に説明し、アコースティックギター、ブラス、ドラムセットの3つの楽器で計算上評価しました。その後、音の周波数領域表現を紹介し、フーリエ変換とスペクトログラムに関するさまざまな理論的な議論を通じて分析しました。これにより、バンドエネルギー比、スペクトル重心、バンド幅、音質係数など、さまざまな周波数領域の特徴が提示され、入力オーディオの特定の特性を効率的に評価するために使用できるようになりました。メルスペクトログラム、ケプストラム係数、ノイズ制御、音声合成など、信号処理アプリケーションにはさらに多くの要素があります。私はこの説明がフィールド内の高度な概念のさらなる探求の基盤となることを望んでいます。
この記事をお楽しみいただけたら幸いです！疑問や提案がある場合は、コメントボックスに返信してください。
お気軽にメールでご連絡ください。
私の記事が気に入った場合は、フォローしてください。
注意：表紙画像以外のすべての画像は、著者によって作成されました。
参考文献
Crest factor. (2023). In Wikipedia. https://en.wikipedia.org/w/index.php?title=Crest_factor&oldid=1158501578
librosa — Librosa 0.10.1dev documentation. (n.d.). Retrieved June 5, 2023, from https://librosa.org/doc/main/index.html
Spectral flatness. (2022). In Wikipedia. https://en.wikipedia.org/w/index.php?title=Spectral_flatness&oldid=1073105086
The Sound of AI. (2020, August 1). Valerio Velardo. https://valeriovelardo.com/the-sound-of-ai/

                  We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
                  
                    audioData scienceDeep DivesMachine learningMusic                  

                  
                  
                    
                      Share:















                    
                  
                  

                  
                    
                      
                    
                    
                      
                    
                  
                  
                        
        
          Was this article helpful?
        

        
          
          
        

        93 out of 132 found this helpful
      
                  Related articles
        
        「BFS、DFS、ダイクストラ、A*アルゴリズムの普遍的な実装」

        このAI研究は、近くの電話によって記録されたキーストロークを聞くことで、95％の正確さでデータを盗むことができるディープラーニングモデルを紹介しています

        「フィル・ザ・ギャップス：フィリピンの2022年貿易ネットワークの隠されたつながりを解明する」

        「生データから洗練されたデータへ：データの前処理を通じた旅 – パート2：欠損値」

        ジオスペーシャルデータ分析のための5つのPythonパッケージ

        システムエンジニアからデータアナリストへのキャリア転換

        「Jupyter AIに会おう Jupyterノートブックで人工知能の力を解き放つ」
                  
                    
                      
                      多段階回帰モデルとシンプソンのパラドックス
                    
                    

                    
                      
                        
                      
                      「AIディープフェイクの作り方（初心者向け）」