「データからドルへ：線形回帰の利用」

Data to Dollars Using Linear Regression

予測分析の魔法を解き明かす

データ駆動型の意思決定は、あらゆる業界の企業にとってゲームチェンジャーとなっています。マーケティング戦略の最適化から顧客の行動の予測まで、データは未開拓の機会を開く鍵です。この記事では、データの洞察を具体的な経済的利益に変換する強力なツールとしての線形回帰の驚異的な可能性とその数学について探求します。

線形回帰は、依存変数(Y)と独立変数(X)の関係を予測するための教師あり機械学習手法です。例えば、株価の予測などに使用されます。

線形回帰の種類

1. 単回帰: ここでは1つの入力列と1つの出力列があります。
2. 重回帰: ここでは複数の入力列と1つの出力列があります。
3. 多項式回帰: データが直線的ではない場合に使用されます。

線形回帰の仮定

1. 従属変数と独立変数の関係は直線的である
2. 変数間にはほとんどまたは全く多重共線性がない
3. 正規分布形式であると仮定される

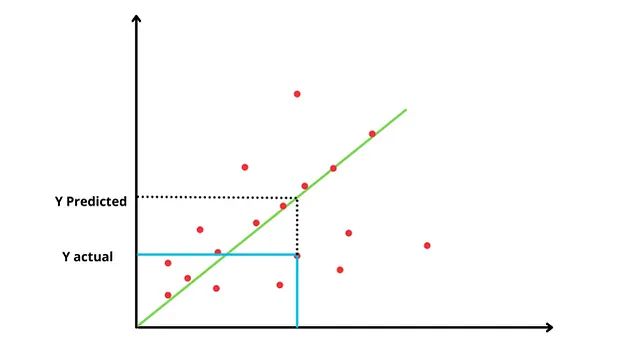
主な目的は、独立変数と従属変数の関係を最小のエラーを持つラインを求めることです。

最適フィットライン: 最大の点を通り、実際の点とラインの間の距離が最小となるラインです。

• 「Amazon SageMaker Canvasによるデータ処理、トレーニング、推論におけるパフォーマンスを70％向上させ、ビジネスの成果を加速させましょう」
• 「AIがインターネット・オブ・シングスの世界をどのように革新しているのか？」
• データサイエンスのためのSQL：ジョインの理解と活用

しかし、最適なラインをどのように見つけるのでしょうか？

まず、データの値の平均を通る水平なラインから始めます。これはおそらく最も適切でないフィットですが、データについて最適なラインを見つけるための出発点となります。この水平なラインでは、x = 0 です。y = mx+c であり、x = 0 なので、y = c となります（最悪の場合、ここではyは従属変数に依存しません）。次のステップでは、このラインの残差の二乗和（SSR）を見つけます。

残差の二乗和 (SSR) = データからラインまでの距離を二乗し、それを合計してSSRの値を求めます。残差はエラーの別名です。

最小のSSRを見つけることを目指します。そのため、水平なラインを回転させ、新しいラインに関してSSRを見つけます。そして、異なる回転のためにこれを繰り返します。

これらのSSRの中で最小のものを考慮し、そのラインをデータに適合させます。最小二乗法として知られるこの方法では、最小二乗がデータに適用されます。

線形回帰の異なるアルゴリズム

1. 最小二乗法(OLS)
2. 勾配降下法: これは最適化技術です

線形回帰の評価指標

• 平均絶対誤差 (MAE): 微分可能ではありません。MAEを求める際に単位をそのまま保持するため、データの解釈が容易であり、外れ値に対しても頑健です。

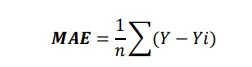
• 平均二乗誤差（MSE）：微分可能ですが、単位が変わると解釈が触れられます。ここでは単位を二乗しています。

• 平方根平均二乗誤差（RMSE）：

解釈性：MAE>RMSE>MSE外れ値に敏感：MSE>RMSE>MAE

• R二乗（R2）：決定係数または適合度です。最も適合した直線と最悪の直線を比較して、どれだけ良いかをチェックします。R2の値は0から1まで変動します。モデルが完全に近づくほど、R2の値は1に近づき、最悪に近づくほど、R2の値は0に近づきます。これは、y変数の変動のうち、x変数で説明できる割合を教えてくれます。

R2 = 説明された変動/全変動R2 = (全変動 – 未説明の変動)/全変動 R2 = 1 – (未説明の変動/全変動)ここで、全変動 = 変動（平均）：(データ-平均)²/n未説明の変動 = 変動（適合）：(データ-直線)²/n

例えば、weight_lostを予測したい場合、calories_intake変数があります。R2が70％の場合、marks変数の変動の70％がhours_studied変数の助けを借りて説明できることを意味します。これは適合度が70％であり、適合度の良さを表しています。今度は、sleeping_hoursという新しい特徴量を追加し、これが目標変数であるweight lostと関連性がない場合でも、R2が増加します。しかし、これは正しくありません。実際にはモデルの精度を増加させ、不要な列をトレーニングするために計算能力を増加させています。

R2の問題：モデルに関与する特徴量が重要ではない場合でも、R2の値は増加します。増加量は小さくても増加するので、減少することはありません。したがって、特徴量が重要ではないため、モデルを不要にトレーニングする必要があります。 したがって、「調整R2」が必要です

• 調整R2：モデルにさらに多くの特徴量を追加すると、R2の値が増加します。なぜなら、SS（res）の値は常に減少するからです。そのため、調整R2は相関性のない属性に罰則を与えます。したがって、属性が相関していない場合にのみR2の値が減少し、それ以外の場合は増加します。

調整R2 = 1 – ((1-R2)(N-1)/N-P-1)N = データポイントの数 P = 独立した特徴量の数

したがって、調整R2は、独立変数が有意であり、従属変数に影響を与える場合にのみ増加します。また、オーバーフィッティングは発生しません。なぜなら、ここでは値に罰則を与えているからです。

読んでくれてありがとう！もしこの記事が気に入ったら、私の他の作品を読んでいただけると嬉しいです。今後ももっとシェアできることを楽しみにしています。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!