「スクラッチからのPythonにおける最急降下法とニュートン法：比較」

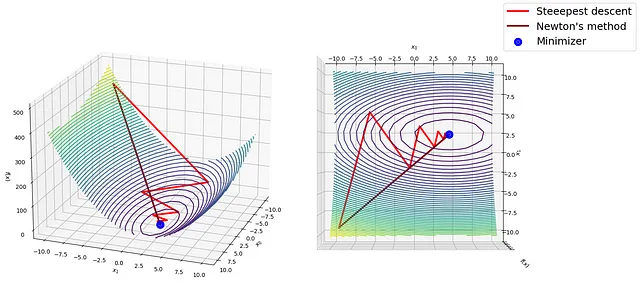
Comparing gradient descent and Newton's method in Python from scratch

目次

1. はじめに
2. 問題の設定と最急降下法
3. ニュートン法
4. 実装
5. 結論と最終的な比較

1. はじめに

前回の投稿では、最適化のための人気のある最急降下法を探求し、Pythonでゼロから実装しました：

Pythonでゼロから最急降下法アルゴリズムを実装する

目次

towardsdatascience.com

この記事では、ニュートン法を紹介し、ステップバイステップで実装しながら最急降下法と比較します。

2. 問題の設定と最急降下法

最適化は、目的関数 f(x) を最小化する変数の集合 x を見つけるプロセスです：

• 「MMDetectionを使用して物体検出モデルのトレーニング方法を学びましょう」
• 「アイデアからAIを活用したビジネスへ：AI＆自動化を活用する中小企業のための5つの重要なステップ」
• 「Hugging Face Transformersを使用したBERT埋め込みの作成」

この問題を解決するために、座標空間で始点を選び、探索方向 p を通じて最小値のより良い近似に向かって反復的に移動します：

この式では：

• x は入力変数です；
• k は現在の反復回数です；
• p は探索方向です；
• α > 0 はステップサイズまたはステップ長です；方向 p にどれだけ移動するかを示します。

探索方向

最急降下法では、現在の反復 xₖ で評価される負の勾配 -∇f(xₖ) が探索方向 pₖ です：

最小値は停留点なので、勾配のノルムが与えられた許容誤差よりも小さい場合にアルゴリズムを停止するのは合理的です。

ステップサイズ

ステップサイズ α は理想的には次の目的関数 φ(α) の最小化器です：

ただし、この追加の最適化課題は実用的ではなく、高価です。その解決には、f(x) と ∇f(x) の多くの評価が必要です。不完全な線探索方法…

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!