「クラスの不均衡：ランダムオーバーサンプリングからROSEへ」

Class Imbalance From Random Oversampling to ROSE

クラスの不均衡問題を形式的に定義し、それに対する直感的な解決策を導出しましょう！

最近、Juliaでクラスの不均衡を解決するためのパッケージ「Imbalance.jl」を作成しています。パッケージの構築中に論文を読んだり、実装を調査したりと、多くの努力を重ねました。一般的なクラスの不均衡問題と、それを解決するために最も人気のあるアルゴリズムのいくつかについて、学んだ内容を共有することが役に立つかもしれないと思いました。具体的には、ナイーブなランダムオーバーサンプリング、ROSE、SMOTE、SMOTE-Nominal、SMOTE-Nominal Continuousが含まれます。この記事では最初の2つに焦点を当てます。

アルゴリズムに入る前に、まずクラスの不均衡を形式的に理解しましょう。

クラスの不均衡問題

ほとんどすべての機械学習アルゴリズムは、一種の経験的リスク最小化として見ることができます。その目的は、いくつかの損失関数Lに対して、パラメータθを見つけることであり、次のように最小化します。

• 深層学習フレームワークの比較
• 「IoT企業のインテリジェントビデオアナリティクスプラットフォームを搭載したAIがベンガルール空港に到着」
• スマートインフラストラクチャのリスク評価における人間とAI・MLの協力

たとえば、線形回帰では二乗損失を、ロジスティック回帰では交差エントロピー損失を、SVMではヒンジ損失を、適応的ブースティングでは指数損失を使用します。

基本的な仮定は、データセット上の経験的リスクを最小化するf_θが、母集団からのランダムサンプルと見なせるデータセット上で、同じ量を最小化するモデルを求めるため、ターゲット関数fに十分近いものであるべきということです。

Kクラスのマルチクラス設定では、経験的リスクを次のように表すことができます。

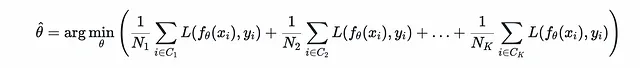
クラスの不均衡は、いくつかのクラスが他のクラスよりもはるかに少ない例を持っている場合に発生します。この場合、対応する項目は和に対して最小限の貢献しかしないため、任意の学習アルゴリズムが主要な和を最小化するような近似解を見つけることが容易になります。これにより、アプリケーションにおいて最も重要な可能性があるマイノリティクラスに関して、真のターゲットfから非常に異なる仮説f_θが得られる可能性があります。

結論として、以下の条件でクラスの不均衡問題が発生します:

1 — トレーニングセットのポイントがクラス間で「公平に」配分されていない。一部のクラスには他のクラスに比べてはるかに少ないポイントがあります。

2— トレーニング後に、そのようなマイノリティクラスに属するポイントでモデルがうまく機能しない。

この問題の深刻度は、そのようなマイノリティクラスがアプリケーションにとってどれだけ重要かに依存します。ほとんどの場合、それらは多数派のクラスよりもはるかに重要です（例：不正なトランザクションの分類）。

クラスの不均衡問題の解決

問題の説明から明らかなように、1つの解決策は、（マイノリティクラスに属する）小さな和の重みを調整することで、学習アルゴリズムがそれらの無視されることを利用した近似解を避けやすくすることです。この目的のために、機械学習アルゴリズムを修正することはしばしば容易です。特に、それが明示的に経験的リスク最小化の形式であり、損失関数に対して等価なものではない場合です。

問題を解決しようとするもう1つのアプローチは、データのリサンプリングです。最も単純な形では、これは重みを割り当てるコスト感度のアプローチと同等であると見なすことができます。次のアルゴリズムを考えてみてください

与えられた: Kクラスの不均衡なデータセットと各クラスの整数求められる: 各クラスのデータが関連する整数に従って複製されたデータセット操作: クラスkの各ポイントをc回繰り返します（cは関連する整数です）

和にプラグインすることで、これがコスト感度のアプローチと同等であることは明らかです。関数の最小化は、それのスカラー正の倍数の最小化と等価であることを思い出してください。

ランダムオーバーサンプリング

上記のアルゴリズムには小さな問題があります。クラスAには900の例があり、クラスBには600の例がある場合、データセットをバランスさせるためにクラスBをオーバーサンプリングするために使用できる整数の倍数はありません。私たちは、整数ではない複製比率に対応するために、ランダムに複製するポイントを選ぶことでアルゴリズムを拡張することができます。たとえば、クラスBに300の例をオーバーサンプリングしてシステムをバランスさせたい場合（比率1.5に相当）、次のようにすることができます…

1 — クラスBからランダムに300のポイントを選ぶ2— それらのポイントを複製する

このアルゴリズムはナイーブなランダムオーバーサンプリングと呼ばれ、形式的には次のことを行います:

1 — 各クラスに生成する必要のあるポイントの数を計算する（与えられた比率から計算）2— クラスXの場合、その数がNxであると仮定し、そのクラスに所属するポイントから代替を含めてNxのポイントをランダムに選択し、それらを新しいデータセットに追加する

これが上記のアルゴリズムと同等であることは明らかであり、またクラスの重み付けも行います。クラスXの比率が2.0の場合、平均して各ポイントはランダムに1回選択されます。

以下は、不均衡なランダムなデータセットの例であり、3つのクラス（0、1、2）のヒストグラムとオーバーサンプリング前後のポイントの散布図を示しています。

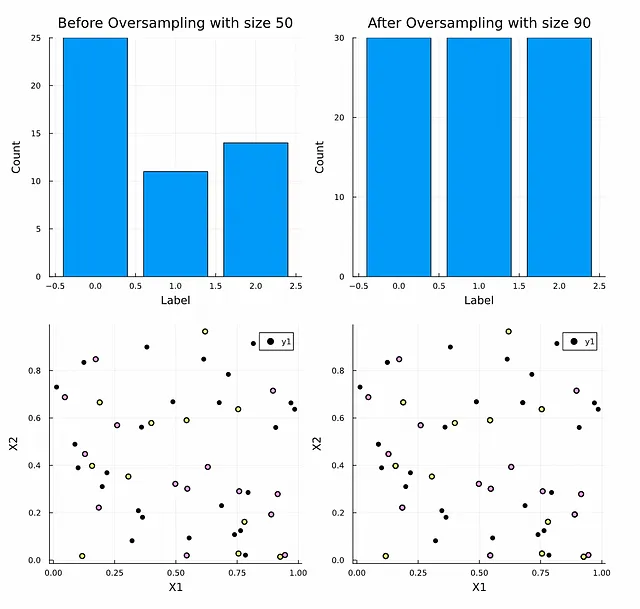
下の2つの図には視覚的な違いがないことに注意してください。すべての生成されたポイントは既存のもののレプリカです。

最後に、少数クラスの複製をランダムに選択する代わりに、多数クラスからポイントをランダムに削除すると、アルゴリズムはナイーブなランダムアンダーサンプリングになります。これには有用なデータを失うという明らかな欠点がありますが、時には「あまり有用ではない」多数クラスからデータを削除することで不均衡の問題を解決し、「より有用な」少数クラスに対してはるかに優れたパフォーマンスを発揮することがあります。この記事と次の記事では、オーバーサンプリングの手法に焦点を当てています。

ランダムオーバーサンプリングの例

自然な形でデータセットに各クラスのポイントを追加すると、ナイーブなランダムオーバーサンプリングよりも良い結果が得られることは理にかなっています。たとえば、次のような場合を考えてみましょう…

• 取引が詐欺かどうかを検出したい
• 1,000件の詐欺取引のデータセットと99万件の有効な取引のデータセットを収集しました

明らかなことですが、既存の1,000件を997,000回繰り返すよりも、少数クラスのデータをさらに998,000件収集して不均衡の問題を解決する方がはるかに優れています。特に後者の場合には、特定のデータに過剰適合するリスクが非常に高いです。

現実的には、少数クラスのためにさらにデータを収集することは一般的には不可能ですが、これは既存の例を繰り返すことよりも優れた方法があることを示しています。収集した追加のデータは、少数クラスに属する基礎となるデータの確率分布に従うことが分かっているので、この確率分布を近似し、実際の例を収集するためにそれからサンプリングすることはどうでしょう。これがランダムオーバーサンプリングの例（ROSE）アルゴリズムが行うことです。

したがって、ROSEは各クラスXに対して確率分布P(x|y=k)を推定し、必要なNxのサンプルをそれから抽出しようとします。このような密度を推定するための一つの方法として、カーネル密度推定があります。これはヒストグラム解析などよりも粗いバージョンから派生することができます。以下にKDEの説明があります:

与えられた: データポイントx 求める: P(x)の推定操作: カーネル関数K(x)を選び、次のようにP(x)を推定します

通常、カーネル関数のスケールを制御したいので、それがP(x)に影響を与えるようになります。より一般的には、次のようになります

本質的には、それは各点の上にカーネル関数を配置し、それらをすべて合計して正規化することで、合計が1になるようにします。

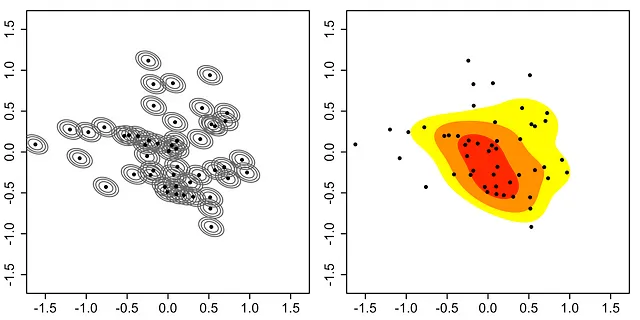
カーネル関数自体の選択はハイパーパラメータです。基本的な性質である滑らかさと対称性を満たしていれば、あまり重要ではないことが示されています。一般的な選択肢は、スケールとしてのσを持つ単純なガウス関数であり、ROSEはこれをKDEに使用します。

ROSEは、次の手順を実行してこの分布からNx個の点をサンプリングします：

• ランダムに点を選択する
• その点にガウス関数を配置する
• ガウス関数からサンプリングする

これはランダムオーバーサンプリングと同様ですが、選択した点を繰り返す代わりに、ランダムに点を選択した後、その点にガウス関数を配置し、ガウス関数から新しい点を生成します。

ROSEでは、Silvermanと呼ばれる経験則に従って帯域幅h（または一般的には高次元のスムージング行列である正規分布の共分散行列パラメータ）を設定し、平均統合二乗誤差を最小化します。特に、

ここで、D_σは各特徴の標準偏差の対角行列、dは特徴の数、Nは点の数です。

Imbalance.jlパッケージでは、この値にもう1つの定数sを乗算して、ハイパーパラメータのオプション制御を許可します。s=1の場合、論文と同じままになり、s=0の場合、ROSEはランダムオーバーサンプリングと同等になります。パッケージを使用して生成された点に対するsの増加の効果を示す次のアニメーションをご覧ください。

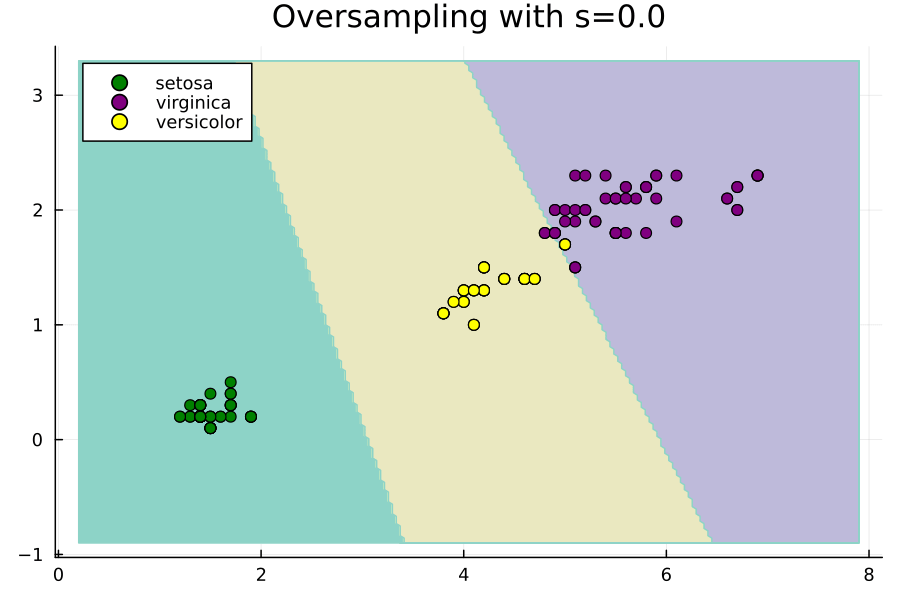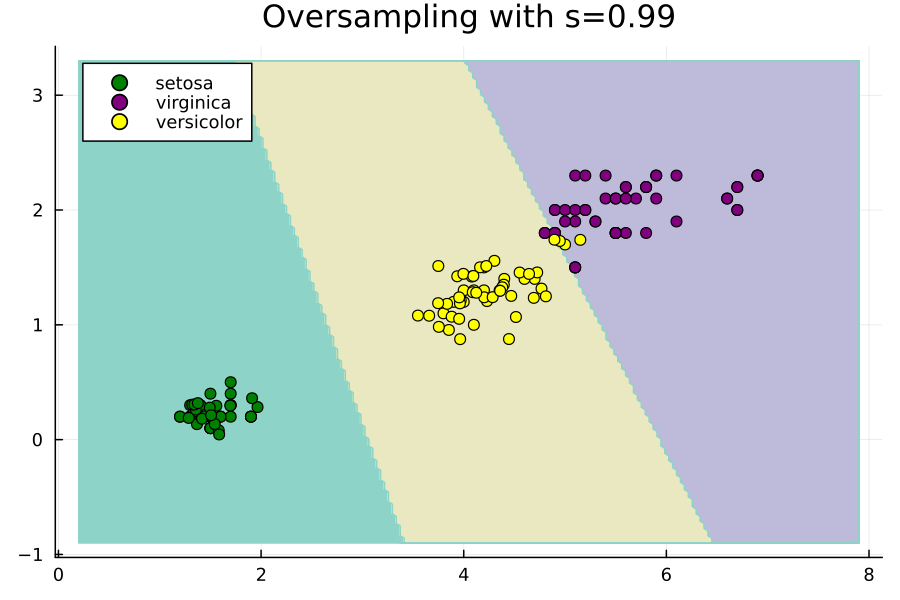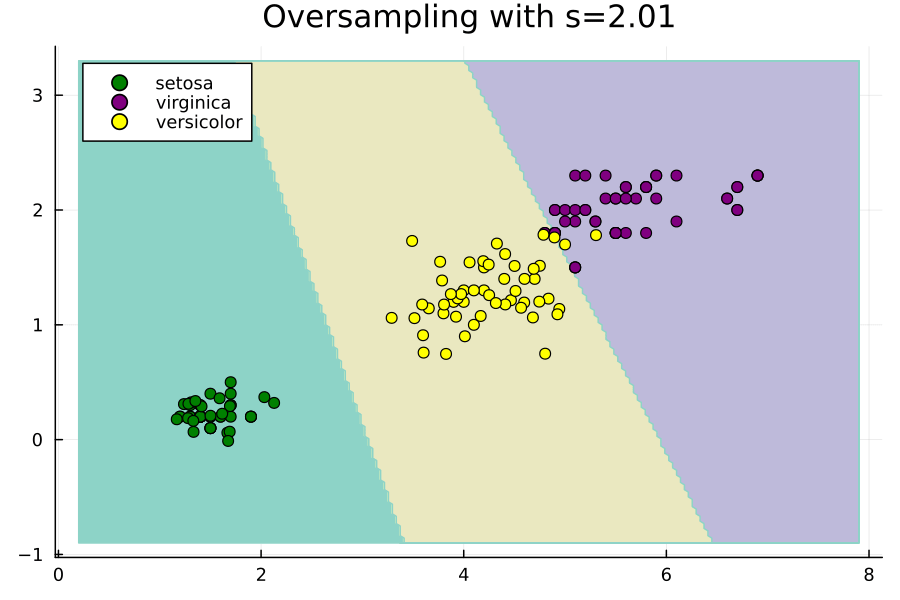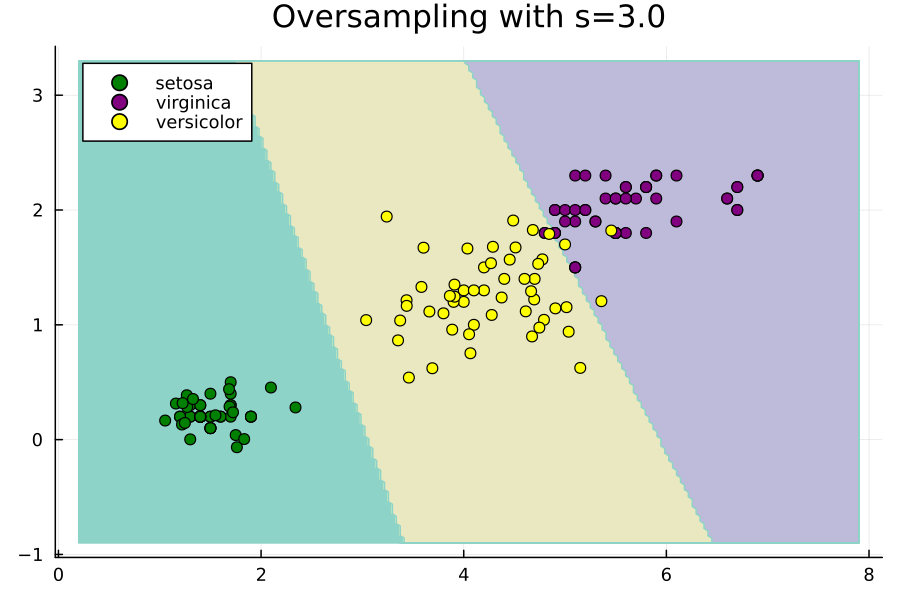
元の点は移動しないことに注意し、sを増やすと、ランダムに選択された各元のために生成された合成点がそれからさらに離れていくことがわかります。

このストーリーが、機械学習のクラス不均衡問題とその解決方法についての理解を深めることになれば幸いです。次のストーリーでは、SMOTE論文で提案されたアルゴリズムについて考えてみましょう。

参考文献：[1] G Menardi, N. Torelli, “Training and assessing classification rules with imbalanced data,” Data Mining and Knowledge Discovery, 28(1), pp.92–122, 2014.

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!