理論から実践へ:k最近傍法分類器の構築
Building k-nearest neighbor classifier From theory to practice.
また別の日、またクラシックなアルゴリズム:k-最近傍法。ナイーブベイズ分類器と同様に、分類問題を解決するための非常にシンプルな方法です。アルゴリズムは直感的でトレーニング時間が最高であり、機械学習のキャリアを開始するときに学ぶのに最適な候補です。ただし、予測を行うときは非常に遅く、特に大規模なデータセットの場合はさらに遅くなります。多くの特徴を持つデータセットの性能も、次元の呪いのために圧倒的ではない場合があります。
この記事では、以下のことを学びます。
- k-最近傍分類器がどのように機能するか
- なぜこのように設計されたのか
- これらの深刻な欠点がある理由、そしてもちろん
- Pythonを使用してNumPyを使って実装する方法。
分類器をscikit-learn準拠の方法で実装するため、自分のカスタムscikit-learn回帰を構築する記事をチェックすることも価値があります。ただし、scikit-learnのオーバーヘッドは非常に小さいため、どちらにせよ追うことができるはずです。
コードは私のGithubで見つけることができます。
理論
この分類器の主なアイデアは驚くほどシンプルです。分類の基本的な質問から直接派生しています。
データポイントxがある場合、クラスcに属する確率は何ですか?
数学の言葉で言えば、条件付き確率p(c|x)を探します。ナイーブベイズ分類器は、一部の仮定を使用してこの確率を直接モデル化しようとしますが、確率の頻度論的な見方を使用してこの確率を計算する別の直感的な方法があります。
確率のナイーブビュー
では、これは今何を意味するのでしょうか?次の簡単な例を考えてみましょう。6面、可能性があるダイスを振って、6を出す確率、つまりp(ロール番号6)を計算したいとします。これをどうやって行うのでしょうか?ダイスをn回振って、6が出た回数を書き留めます。数値6がk回現れた場合、6が出る確率はおよそk/nと言います。ここには何も新しいものやファンシーなものはありませんね。
さて、次に、次のような条件付き確率を計算したいとします。
p(ロール番号6 | 偶数をロールする)
これを解決するためにベイズの定理は必要ありません。ダイスをもう一度振って、奇数の数字のロールを無視してください。これが条件付けが行うこと:結果のフィルタリングです。ダイスをn回振り、m回偶数の数字を見て、そのうちk回が6であった場合、上記の確率はk/nではなくおよそk/mです。
k-最近傍法の動機
問題に戻ります。ベクトルxに特徴を含み、クラスcがある場合のp(c|x)を計算したいのです。ダイスの例と同様に、
- 多くのデータポイントが必要です
- xの特徴を持つデータポイントをフィルタリングする
- これらのデータポイントがクラスcに属する頻度をチェックします。
相対頻度は、確率p(c|x)の推測値です。
ここで問題が見えてきますか?
通常、同じ特徴を持つ多くのデータポイントを持っていません。ほとんど1つ、おそらく2つだけです。たとえば、身長(cm)と体重(kg)の2つの特徴を持つデータセットを想像してください。ラベルは男性または女性です。したがって、x= (x?, x?)、ここでx?は身長で、x?は体重です。cは男性と女性の値を取ることができます。ダミーデータを見てみましょう。
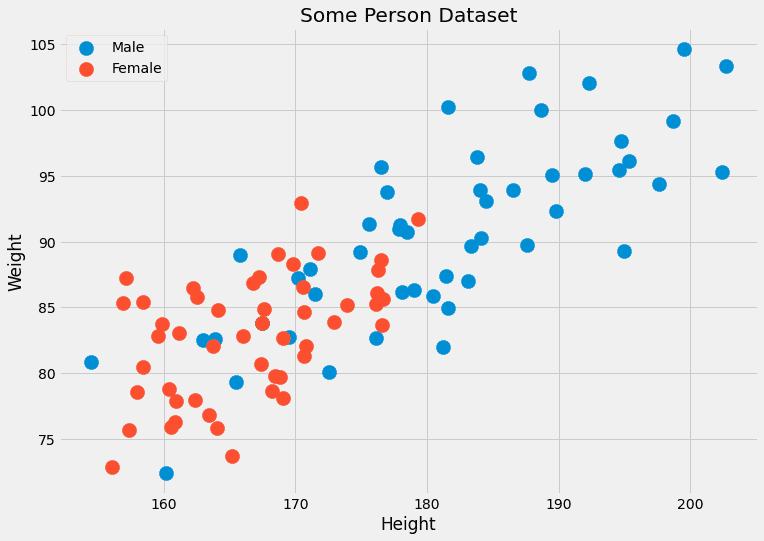
これら2つの特徴は連続しているため、2つ、または数百のデータポイントを持つ確率は限りなくゼロに近いです。
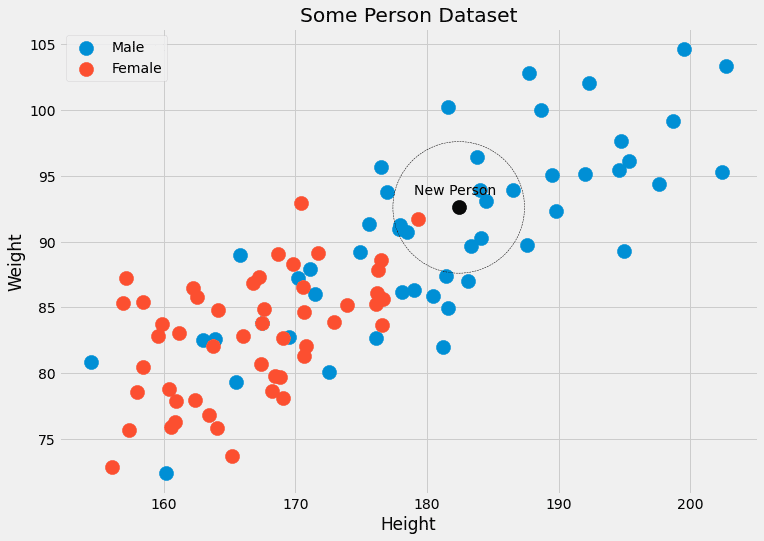
別の問題:見たことのない特徴を持つデータポイント、たとえば(190.1、85.2)のジェンダーを予測するとどうなりますか?これが予測の本当の意味です。これがなぜこのナイーブなアプローチが機能しないかの理由です。代わりに、k-最近傍アルゴリズムが行うのは次のことです。
データポイントの特徴が完全にxであるデータポイントではなく、xに近い特徴を持つデータポイントを使用して、確率p(c|x)を近似しようとします。
ある意味で少し厳格ではありません。 身長=182.4、体重=92.6の多くの人を待って、その性別を確認する代わりに、k-最近傍法では、これらの特性に近い人々を考慮することができます。 アルゴリズムのkは、考慮する人数であり、ハイパーパラメータです。
これらは、学習アルゴリズムによって直接最適化されないパラメータであり、私たちまたはグリッドサーチなどのハイパーパラメータ最適化アルゴリズムが選択する必要があるものです。
アルゴリズム
今、アルゴリズムを説明するために必要なものが全て揃っています。
トレーニング:
- トレーニングデータを整理します。予測時に、この順序により、任意のデータポイントxに対してk個の最も近いポイントを与えることができる必要があります。
- 以上です!😉
予測:
- 新しいデータポイントxに対して、整理されたトレーニングデータのk個の最近傍点を見つけます。
- これらk個の近傍のラベルを集約します。
- ラベル/確率を出力します。
これを実装することはできません。空白を埋める必要があります。
- 整理とは何ですか?
- 接近度をどのように測定しますか?
- 集約するにはどうすればよいですか?
kの値に加えて、これらはすべて選択できるものであり、さまざまな決定により、異なるアルゴリズムが得られます。以下のように答えて、質問を簡単にしましょう。
- 整理=トレーニングデータセットをそのまま保存する
- 近接度=ユークリッド距離
- 集約=平均化
これに対する例を見てみましょう。再び人のデータを持つ画像を確認しましょう。
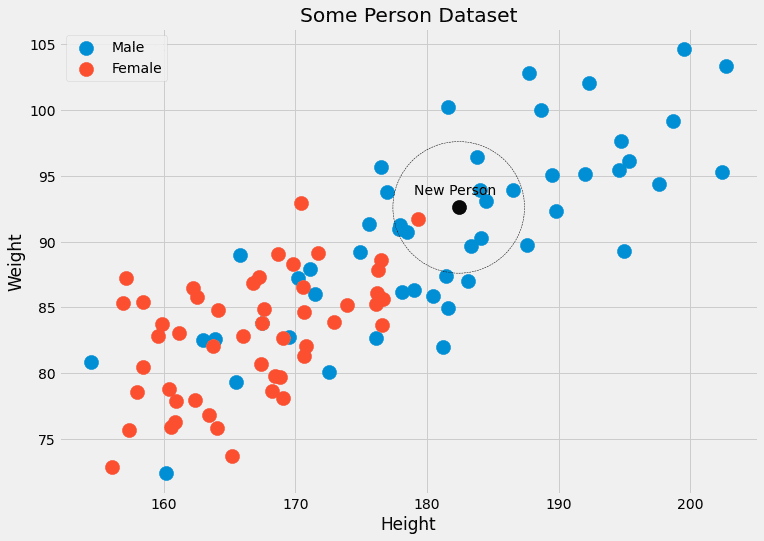
黒点に属する人と最も近いk = 5個のデータポイントが4つの男性ラベルと1つの女性ラベルを持っていることがわかります。したがって、黒点に属する人は、実際には4/5=80%男性であり、1/5=20%女性です。単一のクラスが出力されるようにする場合、男性を返すことができます。問題ありません!
では、実装しましょう。
実装
最も困難な部分は、点に最も近い近傍を見つけることです。
クイックプライマー
Pythonでこれを行う方法の小さな例を示しましょう。
import numpy as np
features = np.array([[1, 2], [3, 4], [1, 3], [0, 2]])
labels = np.array([0, 0, 1, 1])
new_point = np.array([1, 4])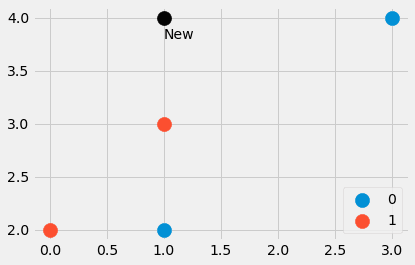
4つのデータポイントと、別の点からなる小さなデータセットを作成しました。最も近い点はどこですか?新しい点のラベルは0または1である必要がありますか?調べてみましょう。入力すると、
distances = ((features - new_point)**2).sum(axis=1)距離=[4, 4, 1, 5]が得られます。これは、new_pointからfeaturesの他のすべてのポイントまでの二乗ユークリッド距離です。素晴らしい!ポイント番号3が最も近く、次に番号1と2のポイントです。 4番目のポイントは最も遠いです。
どのようにして、配列[4,4,1,5]から最も近い点を抽出することができるでしょうか?distances.argsort()が役立ちます。結果は[2,0,1,3]であり、インデックス2のデータポイントが最も小さい(アウトポイント番号3)、次にインデックス0のポイント、次にインデックス1のポイント、最後にインデックス3のポイントが最大であることを示しています。
argsortは、最初の4つの要素が2番目の4つの要素よりもdistances配列に先立つことに注意してください。ソートアルゴリズムによっては、逆の順序になることもありますが、この入門記事ではこれらの詳細には触れません。
たとえば、3つの最も近い隣人を取得したい場合は、
distances.argsort()[:3]を使用して、これらの最も近い点に対応するラベルは、以下のように取得できます。
labels[distances.argsort()[:3]]これにより、[1, 0, 0]が得られます。ここで、1は(1, 4)に最も近い点のラベルであり、0は次に2つの最も近い点に属するラベルです。
それで十分です。本題に入りましょう。
ファイナルコード
コードにはお馴染みのものが多いです。新しい関数はnp.bincountのみで、ラベルの出現回数をカウントします。まず、確率を計算するためのpredict_probaメソッドを実装し、predictメソッドはこのメソッドを呼び出して、最高の確率を持つインデックス(=クラス)をargmax関数を使用して返します。クラスには、0からC -1までのクラスが含まれます。ここで、Cはクラスの数です。
免責事項:このコードは最適化されていません。教育目的のためのみに使用してください。
import numpy as np
from sklearn.base import BaseEstimator, ClassifierMixin
from sklearn.utils.validation import check_X_y, check_array, check_is_fitted
class KNNClassifier(BaseEstimator, ClassifierMixin):
def __init__(self, k=3):
self.k = k
def fit(self, X, y):
X, y = check_X_y(X, y)
self.X_ = np.copy(X)
self.y_ = np.copy(y)
self.n_classes_ = self.y_.max() + 1
return self
def predict_proba(self, X):
check_is_fitted(self)
X = check_array(X)
res = []
for x in X:
distances = ((self.X_ - x)**2).sum(axis=1)
smallest_distances = distances.argsort()[:self.k]
closest_labels = self.y_[smallest_distances]
count_labels = np.bincount(
closest_labels,
minlength=self.n_classes_
)
res.append(count_labels / count_labels.sum())
return np.array(res)
def predict(self, X):
check_is_fitted(self)
X = check_array(X)
res = self.predict_proba(X)
return res.argmax(axis=1)以上です!小さなテストを行って、scikit-learnのk-最近傍分類器と一致するかどうかを確認してみましょう。
コードのテスト
別の小さなデータセットを作成して、テストしてみましょう。
from sklearn.datasets import make_blobs
import numpy as np
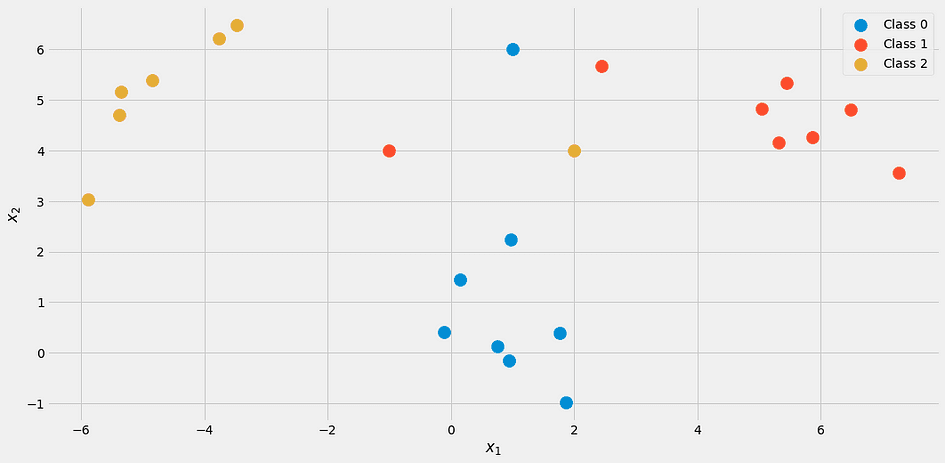
X, y = make_blobs(n_samples=20, centers=[(0,0), (5,5), (-5, 5)], random_state=0)
X = np.vstack([X, np.array([[2, 4], [-1, 4], [1, 6]])])
y = np.append(y, [2, 1, 0])このようになります。
k = 3で当社の分類器を使用して
my_knn = KNNClassifier(k=3)
my_knn.fit(X, y)
my_knn.predict_proba([[0, 1], [0, 5], [3, 4]])次のようになります。
array([[1. , 0. , 0. ],
[0.33333333, 0.33333333, 0.33333333],
[0. , 0.66666667, 0.33333333]])出力を次のように読み取ります。最初の点は100%がクラス1に属しており、2番目の点は各クラスに等しく33%含まれ、3番目の点は約67%がクラス2に属し、33%がクラス3に属しています。
具体的なラベルが必要な場合は、
my_knn.predict([[0, 1], [0, 5], [3, 4]])を試してください。これにより [0, 0, 1] が出力されます。引き分けの場合、実装したモデルでは下位クラスが出力されることに注意してください。つまり、点 (0, 5) はクラス 0 に属すると分類されます。
図を確認すると、それは理にかなっています。しかし、scikit-learn のヘルプを使って自分自身を安心させましょう。
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X, y)
my_knn.predict_proba([[0, 1], [0, 5], [3, 4]])結果:
array([[1. , 0. , 0. ],
[0.33333333, 0.33333333, 0.33333333],
[0. , 0.66666667, 0.33333333]])ふぅ!すべてうまくいっているようです。アルゴリズムの決定境界を確認してみましょう。それが美しいからです。
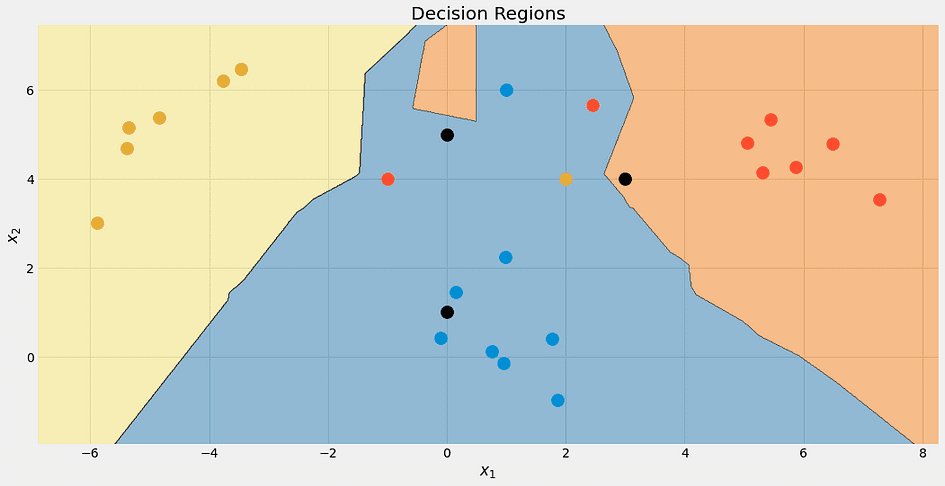
再び、上部の黒い点は完全に青ではありません。それは33%の青、赤、黄色ですが、アルゴリズムは最も低いクラス、つまり青を決定的に選択します。
異なる k の値に対する決定境界をチェックすることもできます。
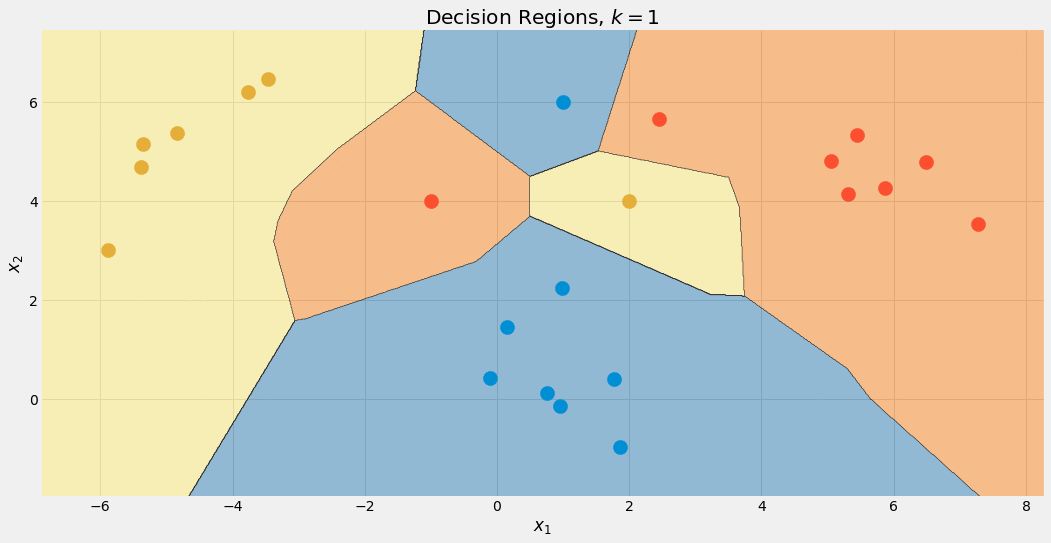
クラスに優先的な扱いがあるため、青い領域が最後に大きくなることに注意してください。k =1 の場合、境界線は混乱しています。モデルは 過剰適合 しています。反対側の極端な場合、k がデータセットのサイズと同じ場合、すべての点が集計ステップに使用されます。したがって、各データポイントには同じ予測が与えられます。つまり、多数派のクラスです。この場合、モデルは 適合不足 しています。最適なスイートスポットはその間にあり、ハイパーパラメータの最適化技術を使用して見つけることができます。
最後まで行く前に、このアルゴリズムが持つ問題を見てみましょう。
k-最近傍法の欠点
問題は次のとおりです。
- 最近傍の検索には多くの時間がかかります。特に私たちの単純な実装ではそうです。新しいデータポイントのクラスを予測する場合、データセット内のすべての他の点と比較する必要があります。これは遅いです。高度なデータ構造を使用してデータをより良い方法で整理する方法がありますが、問題は依然として存在します。
- 問題 1 に続いて:通常、より速く、より強力なコンピューターでモデルをトレーニングし、その後により弱いマシンにモデルを展開できます。たとえば、ディープラーニングを考えてみてください。しかし、k -最近傍法の場合、トレーニング時間が簡単であり、重い作業は予測時間に行われるため、私たちが必要とするものではありません。
- 最近傍がまったく近くない場合、どうなりますか?それらは何も意味しません。これは、特徴が少数しかないデータセットでもすでに起こる可能性があるが、より多くの特徴がある場合はこの問題が大幅に増加するということを意味します。これは、次元の呪いとしても知られています。Cassie Kozyrkov のこの投稿に素敵な可視化があります。
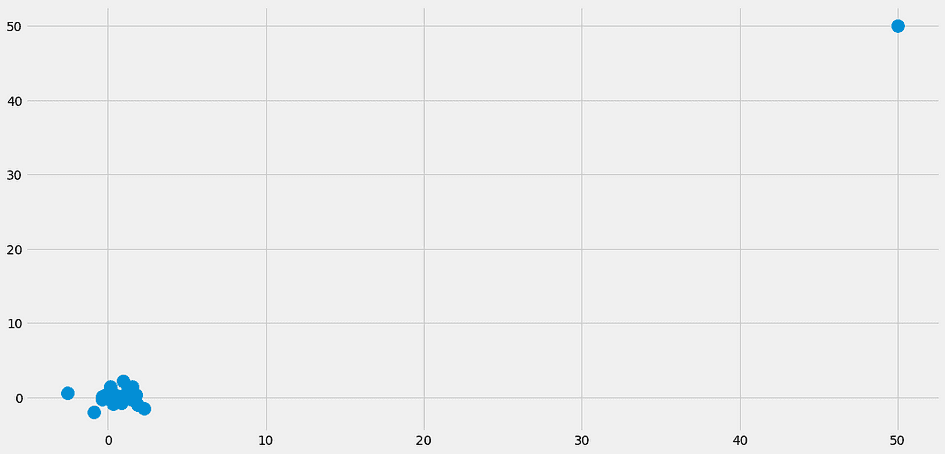
特に問題 2 のために、k -最近傍法はあまり使われていません。それでも知っておくべき素晴らしいアルゴリズムであり、小さなデータセットに使用することもできます。しかし、何百万ものデータポイントがあり、何千もの特徴がある場合、問題が発生します。
結論
この記事では、k -最近傍法分類器の動作方法と、その設計が意味を持つ理由について説明しました。それは、x に最も近いデータポイントを使用して、データポイント x がクラス c に属する確率をできるだけ正確に推定しようとするものです。非常に自然なアプローチであり、そのため、このアルゴリズムは通常、機械学習コースの最初に教えられます。
k-最近傍法回帰器を構築するのは本当に簡単であることに注意してください。クラスの出現回数を数える代わりに、最も近い隣人のラベルを平均化して予測を得るだけです。自分でこれを実装することができます。それはわずかな変更です!
その後、私たちはscikit-learn APIを模倣して、簡単な方法で実装しました。これは、scikit-learnのパイプラインやグリッドサーチでもこの推定器を使用できることを意味します。ハイパーパラメータkもグリッドサーチ、ランダムサーチ、またはベイジアン最適化を使用して最適化できるという大きな利点があります。
ただし、このアルゴリズムにはいくつかの深刻な問題があります。大規模なデータセットには適しておらず、弱いマシンに展開して予測を行うことはできません。次元の呪いへの感受性とともに、理論的には素晴らしいアルゴリズムですが、小さなデータセットにしか使用できません。
Dr. Robert Küblerは、METRO.digitalのデータサイエンティストであり、Towards Data Scienceの著者です。
元記事。許可を得て再掲載。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles




