モデルの精度にだまされない方法
Avoiding being deceived by the accuracy of the model.
バイナリ分類モデルのメトリクスとその適切な使用方法に関するビジュアルガイド

背景 – 表面的にはシンプル
分類モデルの性能評価に使用されるメトリクスは、数学的な観点からは比較的簡単です。しかし、多くのモデラーやデータサイエンティストがこれらのメトリクスを明確に説明するのに苦労し、さらに誤った方法で適用していることがよく見られます。これは簡単な間違いです。これらのメトリクスは表面的にはシンプルに見えますが、問題の領域によっては重大な意味を持つことがあります。
この記事は、一般的な分類モデルのメトリクスを説明するためのビジュアルガイドとして機能します。定義と使用例を探求し、メトリクスが不適切に使用される場所を強調します。
可視化に関する簡単な注記
各可視化は、分類したい対象を表す90のサンプルで構成されています。青のサンプルは負のサンプルを示し、赤は正のサンプルを示します。紫のボックスは、正のサンプルを予測しようとするモデルです。このボックス内のものは、モデルが正と予測するものです。
これが明確になったところで、定義に入りましょう。
適合率と再現率
多くの分類タスクでは、適合率と再現率の間にトレードオフがあります。再現率を最適化すると適合率が犠牲になることがしばしばあります。しかし、これらの用語は実際には何を意味しているのでしょうか?数学的な定義から始めて、次に視覚的な表現に移りましょう。
適合率 = TP/ (TP + FP)
再現率 = TP/(TP + FN)
ここで、TP = 真陽性の数、FP = 偽陽性の数、FN = 偽陰性の数です。
以下のチャートに焦点を当てましょう。このチャートには4つの正のサンプルがあります。モデルの正の予測は、チャート上のボックスで表されます。チャートを観察すると、モデルは4つの正のサンプルを正しく予測していることがわかります- これは、すべての正のサンプルがボックス内にあることで確認できます。モデルの再現率をチャートから計算すると、ボックス内の正のケースの数(TP = 4)を正のケースの合計数(TP = 4 + FN = 0)で割ることで求めることができます。
FNは0なので、ボックスの外には正のケースはありません。

適合率も同様に説明することができます。ボックス内の正のケースの数(TP = 4)をボックス内のケースの合計数(TP = 4 + FP = 6)で割るだけです。簡単な計算により、モデルの適合率はわずか40%であることがわかります。
モデルは再現率が高くても適合率が低くなる場合があることに注目してください。以下のチャートはこのことを示しており、再現率はわずか50%、一方で適合率は100%です。これらの数値にたどり着く方法を内面化できるか試してみてください。
これを理解するためのヒントを示します。偽陰性の数は2です。なぜなら、ボックスの外には2つの正のサンプルがあるからです。
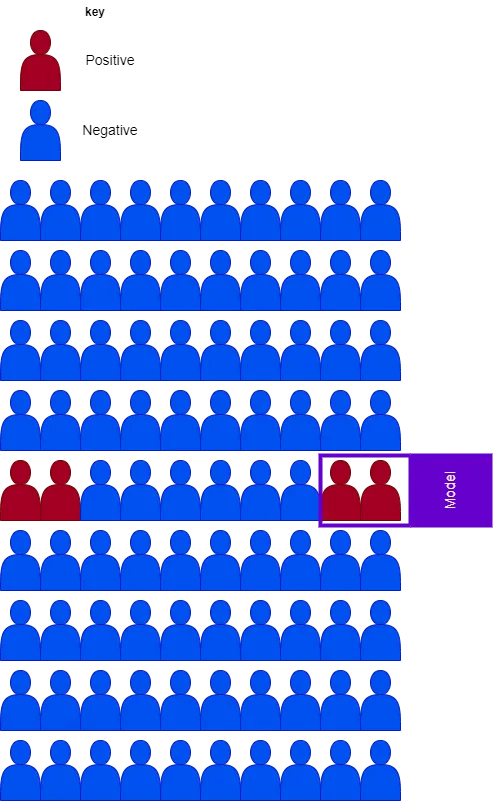
偽陽性率と真陰性率
偽陽性率(FPR)は、その名前から推測するに比較的直感的に理解できるかもしれません。しかし、他のメトリクスと同様に、この概念を探求しましょう。数学的には、FPRは次のように表されます:
FPR = FP/(FP + TN)
ここで、TNは真陰性サンプルの数を表します。
再び最初の画像を見てみると、FPRはボックス内の負のサンプルの数(FP=6)を負のサンプルの総数(FP=6 + TN=80)で割ることで決定できます。最初の画像では、偽陽性率はわずか7%であり、2番目の画像では0%です。なぜそうなるのか考えてみてください。
覚えておいてください、ボックス内のサブジェクトはモデルが陽性と予測したものです。したがって、ボックスの外の負のサンプルは、モデルが陰性と識別したものです。
真陰性率(TNR)は次の式を使って計算できます:
TNR = TN/(TN + FP)
TNRは常に偽陽性率の1から引いた値です。
正確性
正確性はモデルのパフォーマンスを評価する際に広く使われる用語ですが、実際にはどういう意味なのでしょうか?数学的な定義から始めましょう:
正確性 = (TP + TN) / (TP + TN + FP + FN)
以前に適用したロジックを使って、最初の画像のモデルの正確性は93%、2番目の画像の正確性は97%と計算できます(自分で導いてみてください)。正確性がいくつかのケースで欺瞞的なメトリックになりうる理由について、次で詳しく探っていきます。
メトリックの正しい使用
なぜこれらのメトリックに関心を持つのでしょうか?それは、モデルのパフォーマンスを評価する方法を提供してくれるからです。これらのメトリックを理解すると、モデルに関連する商業価値をさえ決定することができます。だからこそ、適切な(および不適切な)使用方法について良い直感を持つことが重要です。これを説明するために、分類タスクの一般的なシナリオであるバランスの取れたデータセットと不均衡なデータセットを簡単に調査してみましょう。
不均衡なデータセット
先に描かれた図は不均衡な分類タスクの例です。単純に言えば、不均衡なタスクでは、陽性サブジェクトの表現が陰性サブジェクトに比べて少ないです。クレジットカードの不正検知や顧客の離反予測、スパムフィルタリングなど、バイナリ分類の商業的なユースケースの多くがこのカテゴリに該当します。不均衡な分類のために選択するメトリックが間違っていると、モデルのパフォーマンスについて過度に楽観的な信念を持つことがあります。
不均衡な分類の主な問題は、真陰性サンプルの数が高く、偽陰性サンプルの数が少ない可能性があることです。例を挙げるために、別のモデルを考えて不均衡なデータで評価してみましょう。モデルが単純にすべてのサブジェクトを陰性と予測するという極端なシナリオを作成することができます。

このシナリオで各メトリックを計算してみましょう。
- 正確性 : (TP=0 + TN=86)/(TP=0 + TN=86 + FP=0 + FN=4) = 95%
- 適合率 : (TP=0) /(TP=0 + FP=0) = undefined
- 再現率 : (TP=0) / (TP=0 + FN=4) = 0%
- FPR : (FP=0) / (FP=0 + TN=86) = 0%
- TNR : (TN=86) / (TN=86 + FP=0) = 100%
正確性、FPR、およびTNRの問題がより明確になってきたはずです。不均衡なデータセットで作業している場合、高精度のモデルを作成しても、実際の展開ではパフォーマンスが低い可能性があります。前の例では、モデルは陽性サブジェクトを検出する能力を持っていませんが、正確度は95%、FPRは0%、完全なTNRを達成しています。
さあ、このようなモデルを医療診断や不正検知に展開してみてください。明らかに無意味で、場合によっては危険です。この極端な例は、不均衡なデータ上で動作するモデルのパフォーマンスを評価するために正確性、FPR、およびTPRなどのメトリックを使用することの問題を示しています。
バランスの取れたデータセット
バランスの取れた分類問題では、不均衡な場合よりも潜在的な真陰性の数がはるかに少なくなります。

「非差別的」モデルをバランスの取れたケースに適用すると、以下の結果が得られます:
- 正解率:(TP=0 + TN=45) / (TP=0 + TN=45 + FP=0 + FN=45) = 50%
- 適合率:(TP=0) / (TP=0 + FP=0) = 定義不明
- 再現率:(TP=0) / (TP=0 + FN=45) = 0%
- 偽陽性率:(FP=0) / (FP=0 + TN=45) = 0%
- 真陰性率:(TN=45) / (TN=45 + FP=0) = 100%
他のすべてのメトリックは同じままですが、モデルの正解率は50%に低下し、モデルの実際のパフォーマンスをより示唆するものとなっています。ただし、適合率と再現率がなければ、正解率だけでは騙される可能性があります。
ROC曲線と適合率-再現率曲線
ROC曲線は、2値分類モデルのパフォーマンス評価によく使用される手法です。ただし、不均衡なデータセットを扱う場合、過剰に楽観的な結果を提供することがあります。
ROCと適合率-再現率曲線の簡単な概要:異なる決定閾値に対して分類メトリックを相互にプロットしています。一般的に、曲線の下の面積(AUC)を測定し、モデルのパフォーマンスの指標とします。ROCと適合率-再現率曲線について詳しく学ぶには、リンクを参照してください。
ROC曲線が過剰に楽観的であることを示すために、Kaggleから取得したクレジットカードの不正データセットを使用して分類モデルを構築しました。データセットは284,807の取引からなり、そのうち492件が不正です。
注:データはOpen Data Commonsライセンスに従って商業目的および非営利目的で許可なく使用できます。

ROC曲線を調べると、この曲線の下の面積が0.97であるため、モデルのパフォーマンスが実際よりも良いと思い込まれる可能性があります。先に見たように、不均衡な分類問題では、偽陽性率は過剰に楽観的になることがあります。
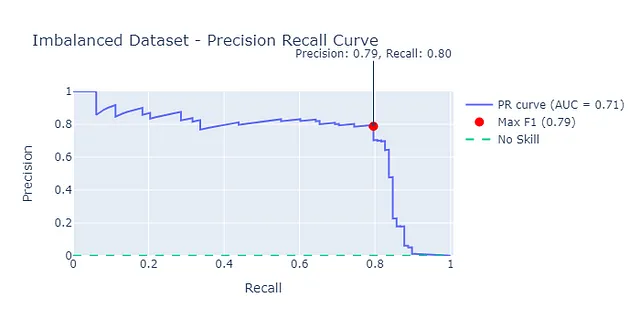
より堅牢なアプローチは、適合率-再現率曲線を利用することです。これにより、モデルのパフォーマンスのより堅牢な推定値が得られます。ここでは、適合率-再現率曲線の下の面積(AUC-PR)が0.71となります。
不正取引と非不正取引が50:50のバランスの取れたデータセットを取ると、AUCとAUC-PRがより近くなることがわかります。


これらのチャートを生成するためのノートブックは、私のGitHubリポジトリで利用できます。
不均衡なデータセット上の分類モデルのパフォーマンスを向上させる方法があります。これについては、シンセティックデータに関する私の記事で探求しています。
シンセティックデータは機械学習のパフォーマンスを向上させることができるのか?
不均衡データセット上のモデルパフォーマンスを向上させるためのシンセティックデータの能力の調査
towardsdatascience.com
結論
分類モデルのメトリクスを理解することは、数式を超えるものです。各メトリクスがどのように使用されるべきか、そしてバランスの取れたデータセットと不均衡なデータセットの両方に対するそれらの影響も理解する必要があります。一般的な指針として、真陰性または偽陰性に基づいて計算されるメトリクスは、不均衡なデータセットに適用されると過度に楽観的になる可能性があります。このビジュアルツアーがあなたに直感的な理解を与えたことを願っています。
非技術的な利害関係者にアプローチを説明するために、このビジュアルな説明が便利だと感じました。このアプローチを共有したり、借用したりしてください。
LinkedInで私をフォローしてください
私からのさらなる洞察を得るためにVoAGIに登録してください:
私の紹介リンクでVoAGIに参加する- John Adeojo
データサイエンスのプロジェクト、経験、専門知識を共有し、あなたの旅をサポートします。VoAGIには次のようにサインアップできます…
johnadeojo.medium.com
AIやデータサイエンスをビジネスの運用に組み込むことに興味がある場合は、無料の初回相談を予約することをお勧めします:
オンライン予約 | データ志向ソリューション
当社のデータサイエンティストおよび無料相談を通じて、ビジネスが野心的な目標を達成するための専門知識をご覧ください。
www.data-centric-solutions.com
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
