AUCとHarrellのCに対する直感
AUCとHarrellのCに対する直感
グラフィカルアプローチ

機械学習や予測モデリングの領域に足を踏み入れた全ての人は、モデルのパフォーマンステストの概念に直面します。教科書では、一般的には回帰分析のMSE(平均標準誤差)や、正確さ、感度、精度などのさまざまなパフォーマンス指標を持つ分類が最初に学習されます。正解/不正解の予測の割合として算出されるAccuracyは非常に直感的ですが、ROC AUCは初めて目にすると難解に思えることもあります。それにもかかわらず、これは予測モデルの品質を評価するために頻繁に使用されるパラメータです。まずはその仕組みを解説し、詳細な部分を理解しましょう。
まずはAUCを理解しましょう
あるクラスに属するサンプルの確率を予測する二値分類器を構築したと仮定しましょう。既知クラスのテストデータセットは、次の結果を示し、混同行列にまとめ、表により詳細に報告されます。ここでは、サンプルはクラスP(陽性)であると予測される確率によってソートされています。
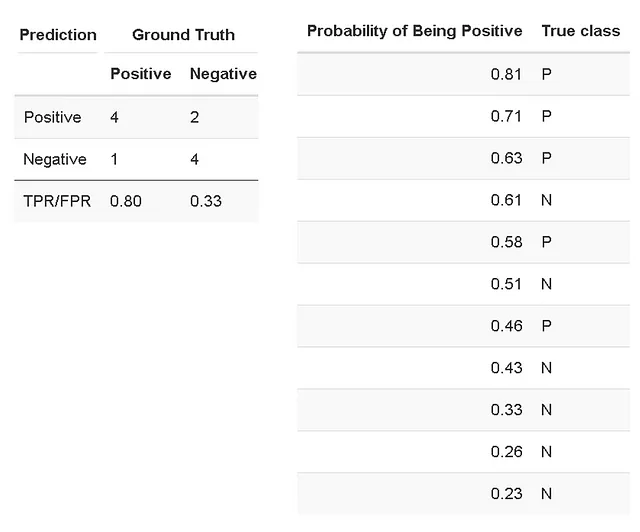
ROC AUCはROC(受信者操作特性)曲線の下の面積として定義されます。ROC曲線は、真陽性率(TPR)と偽陽性率(FPR)のプロットです[Wikipedia]。TPR(感度とも呼ばれる)は、すべての陽性ケースのうち正しく識別された陽性ケースの割合です。この場合、TPRは5つのうち4つ(5つのケースのうち4つが正しく陽性として分類されました)で計算されます。FPRは、誤って陽性として分類された負のケース(偽陽性)の数と実際の負のケースの総数の比率として計算されます。この場合、FPRは6つのうち2つ(6つの負のケースのうち2つが誤って陽性として分類されました)で計算されます(「陽性」の閾値を0.5の確率に設定した場合)。
TPRとFPRの値からROC曲線をプロットし、AUC(曲線下の面積)を計算できます:
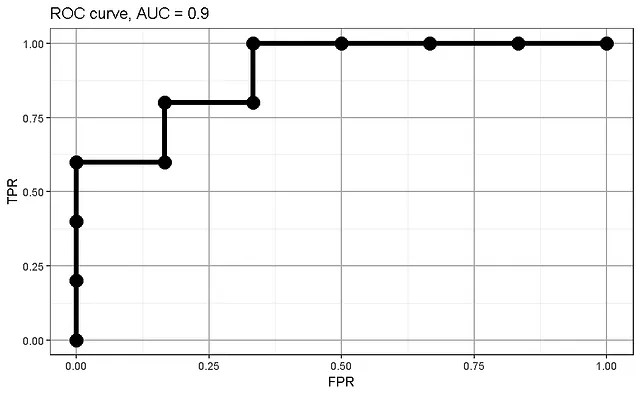
AUC曲線の個々のTPR/FPR値はどこから来たのでしょうか?それについては、確率テーブルを考慮し、各サンプルのTPR/FPRを計算します。ここでは、テーブルで与えられた確率をサンプルが陽性であると見なす確率として設定します。通常のレベルである0.5を超えても、通常「陰性」と宣言されるサンプルにも引き続き陽性を割り当てます。以下、この手順を例に従って説明します:
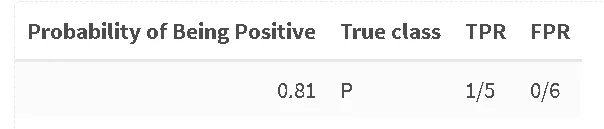
5つの陽性サンプルのうち1つが、しきい値0.81で陽性として正しく分類されましたが、陰性サンプルはありません。次に最初の陰性例に出会うまで続けます:
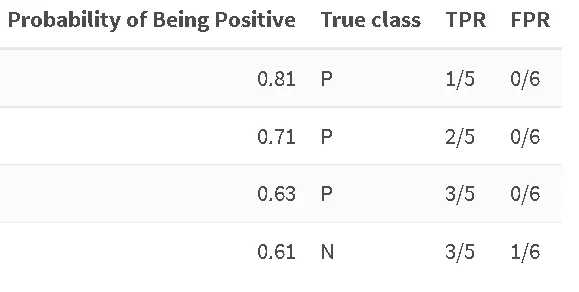
ここでは、TPRは前の値で停滞します(5つの陽性サンプルのうち3つが正しく予測されました)、しかしFPRは増加しました。6つの陰性サンプルのうち1つを誤って陽性クラスに割り当てました。最後まで続けます:
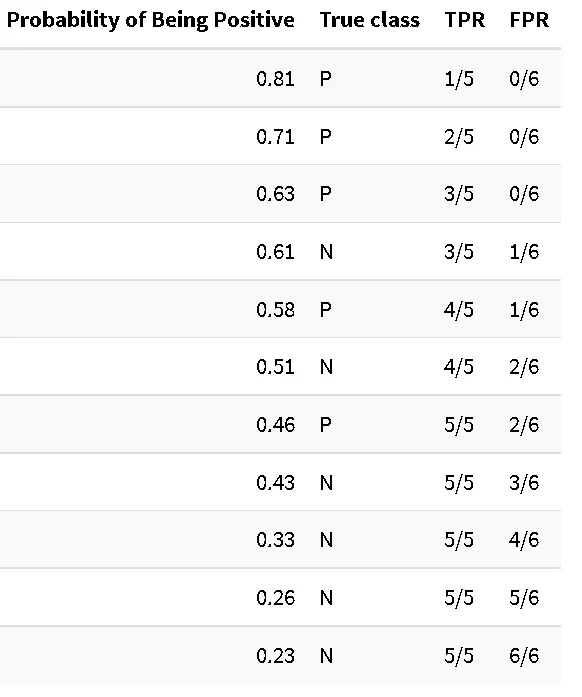
さあ、ROC曲線を作成するために使用される完全なテーブルに到着しました。
なぜHarrellのCはAUCそのものなのか
では、HarrellのC指数(コンコーダンス指数またはC指数とも呼ばれる)はどうでしょうか?特定のタスクとして、特定の病気(例:がん)の発生時に死亡を予測することを考えてみてください。最終的には、すべての患者ががんにかかわらず死亡しますので、単純な2値分類器はあまり役に立ちません。生存モデルは、結果(死亡)までの期間を考慮に入れます。イベントが早く発生するほど、個人のリスクは高くなります。生存モデルの品質を評価する場合、C指数(またはコンコーダンス、またはHarrellのCとも呼ばれます)を見ます。
C指数の計算を理解するために、許容ペアとコンコーダントペアという2つの新しい概念を紹介する必要があります。許容ペアは、観察中に異なる結果を持つサンプル(例:患者)のペアです。つまり、実験が行われている間に、そのペアのうちの1人の患者が結果を経験し、他の患者は検閲されました(まだ結果に達していません)。これらの許容ペアは、リスクスコアが高い個人がイベントを経験したかどうか、検閲された個人がまだイベントを経験していないかどうかを分析されます。これらのケースはコンコーダントペアと呼ばれます。
少し簡略化しますが、C指数はコンコーダントペアの数を許容ペアの数で割った比率として計算されます(単純化のためにリスクのタイは省略します)。前述の例を見てみましょう。リスクの確率ではなくリスクを計算する生存モデルを使用したと仮定します。次の表には許容ペアのみが含まれています。列「コンコーダンス」は、リスクスコアが高い患者がイベントを経験した場合(私たちの「陽性」グループの1つである場合)、1に設定されます。IDは、前のテーブルの行番号です。個人4と5または7の比較に特に注意してください。
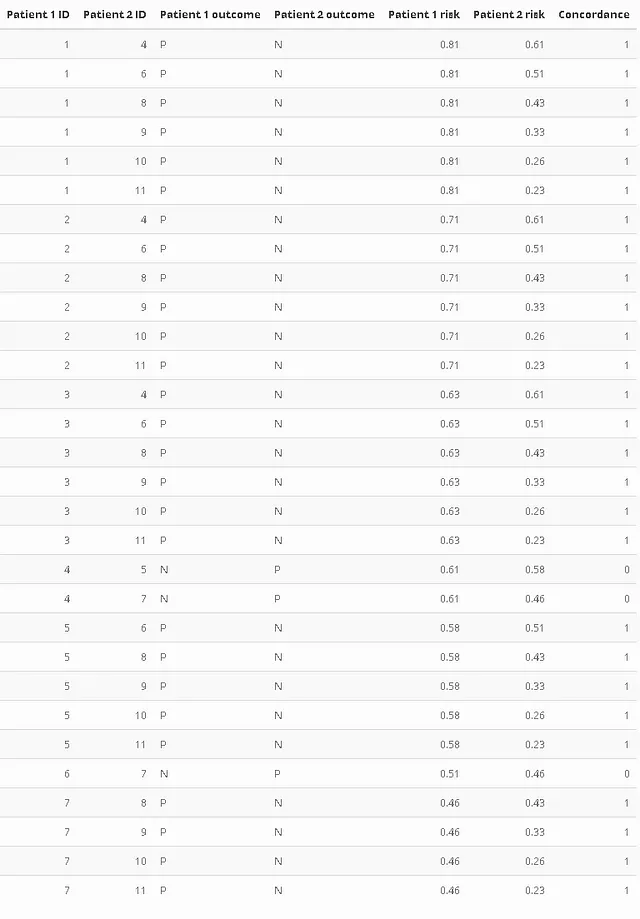
これにより、30個の許容ペアのうち27個のコンコーダントペアが残ります。比率(単純化されたHarrellのC)はC = 0.9であり、以前に計算したAUCを思い起こさせるものです。
Carringtonらによって提案されたように、C統計量が計算される方法を可視化するコンコーダンス行列を作成することができます。このプロットは、実際の陽性のリスクスコアと実際の陰性のリスクスコアを示し、正しくランク付けされたペアの割合(緑)がすべてのペア(緑+赤)の中でどれだけであるかを表示します。各グリッドスクエアをサンプルの表現として解釈すると:
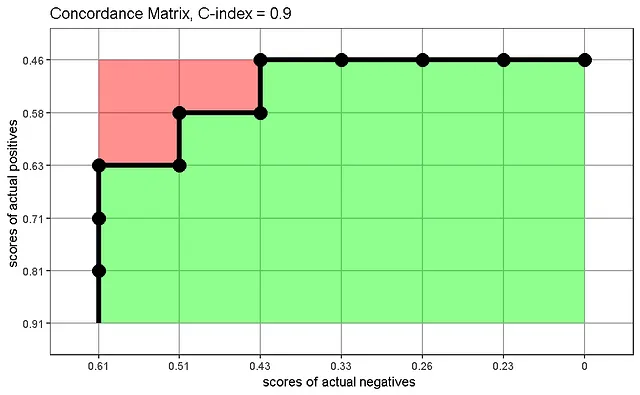
コンコーダンス行列は、正しくランク付けされたペアが右下に向かってコンコーダンスするように、ランク付けが間違っているペアが左上に向かっていること、そしてその間に境界線があることを示しています。これは以前に見たROC曲線とまったく一致します。
ROC曲線とコンコーダンス行列を構築するプロセスを展開してみると、類似性が認識できます:どちらの場合も、サンプルを確率/リスクスコアに基づいてランク付けし、ランキングが正しいかどうかを確認しました。分類のための確率の閾値を高く設定するほど、偽陽性が増えます。実際の陽性ケースのリスクが低いほど、実際の陰性ケースが誤って陽性と分類される可能性が高くなります。ランク付けされたデータを適切にプロットすると、形状と面積が同じである曲線が生成され、それをAUCまたはHarrellのCと呼びます(文脈による)。
この例がAUCとHarrellのCの直感を開発するのに役立ったことを願っています。
謝辞
これら2つのパラメータを比較するアイデアは、Advanced Machine Learning Study Groupのミートアップ中の有意義な議論から生まれました。Torstenに感謝!
参考文献: Carrington, A.M., Fieguth, P.W., Qazi, H. et al. A new concordant partial AUC and partial c statistic for imbalanced data in the evaluation of machine learning algorithms. BMC Med Inform Decis Mak 20, 4 (2020). https://doi.org/10.1186/s12911-019-1014-6
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
