「Pythonにおける記述統計と推測統計の適用」

Application of Descriptive and Inferential Statistics in Python

 

統計学は、データの収集やデータ分析からデータの解釈までを含む分野です。これは不確実性に直面した際に関係者が判断を下すための研究分野です。

統計学の主要な2つの分野は、記述統計学と推測統計学です。記述統計学は、サマリー統計、可視化、および表など、さまざまな方法を使用してデータの要約を行う分野です。一方、推測統計学はデータのサンプルに基づいて集団全体の一般化に関するものです。

この記事では、Pythonの例を使って記述統計学と推測統計学のいくつかの重要な概念を紹介します。さあ始めましょう。

• 『リンゴールド・ティルフォードアルゴリズムの解説とウォークスルー』
• 「ギザギザしたCOVIDチャートの謎を解決する」
• 「社会教育指数は学校卒業者の結果にどのような影響を与えるのか？ – Rとbrmsを用いたベイズ分析」

 

記述統計学

 

前述のように、記述統計学はデータの要約に焦点を当てています。これは生データを意味のある情報に変換する科学です。記述統計学はグラフ、表、またはサマリー統計を使用して行うことができます。ただし、サマリー統計が最も一般的な方法なので、これに焦点を当てます。

この例では、次のデータセットを使用します。

import pandas as pd
import numpy as np
import seaborn as sns

tips = sns.load_dataset('tips')
tips.head()

 

 

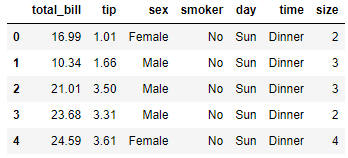
このデータを使用して記述統計学を探求します。サマリー統計では、次の2つの最も使用されるものがあります：中心傾向の指標およびばらつきの指標。

 

中心傾向の指標

 

中心傾向はデータ分布またはデータセットの中心です。中心傾向の指標は、データの中心位置を取得または説明するための活動です。中心傾向の指標は、データの中心位置を定義する単一の値を提供します。

中心傾向の指標には、次の3つの人気のある測定方法があります：

 

1. 平均値

 

平均値は、データの最も一般的な値を表す単一の値を生成する方法です。ただし、平均値は必ずしもデータ内で観察される値ではありません。

平均値は、データ内の既存の値の合計を取り、その数で割って計算することができます。平均値は次の式で表すことができます：

   

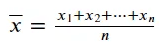
Pythonでは、次のコードでデータの平均値を計算することができます。

round(tips['tip'].mean(), 3)

 

2.998

 

pandasのシリーズ属性を使用してデータの平均値を取得することができます。データを読みやすくするためにデータを丸めています。

平均値は、外れ値に影響を受けやすいため、中心傾向の指標としては欠点があり、実際の状況を最適に表すとは限りません。偏った場合には、中央値を使用することができます。

 

2. 中央値

 

中央値は、データを並べ替えた場合に真ん中に位置する単一の値であり、データの中心位置（50%）を表します。中央値は中心傾向の測定としては、外れ値や偏った値が強く影響しないため、偏ったデータの場合には好ましい指標です。

中央値は、すべてのデータ値を昇順に並べ替え、真ん中の値を見つけることで計算されます。データ値の数が奇数の場合、中央値は真ん中の値ですが、データ値の数が偶数の場合、中央値は2つの真ん中の値の平均です。

Pythonを使用して中央値を計算するには、次のコードを使用します。

tips['tip'].median()

 

2.9

 

3. 最頻値

 

最頻値は、データ内で最も頻繁に出現する値です。データには単一の最頻値（単峰性）、複数の最頻値（多峰性）、または最頻値がない場合（繰り返し値がない場合）があります。

モードは通常、カテゴリカルデータに使用されますが、数値データでも使用することができます。ただし、カテゴリカルデータの場合、モードのみを使用することがあります。これは、カテゴリカルデータには平均値や中央値を計算するための数値がないためです。

以下のコードでデータのモードを計算することができます。

tips['day'].mode()

 

  結果はカテゴリカルな値を持つシリーズオブジェクトです。データのモードである’Sat’の値のみが表示されます。

 

ばらつきの指標

 

ばらつき（または変動性、分散）の指標は、データの値のばらつきを表すための測定です。この測定は、データ値がデータセット内でどのように変動するかに関する情報を提供します。一般的に、中心傾向の指標と組み合わせて使用され、全体的なデータ情報を補完します。

ばらつきの指標は、中心傾向の指標の出力がどれほど良いかを理解するのにも役立ちます。たとえば、データのばらつきが大きいと、観測されたデータとデータの平均値の間に大きな偏差があることを示す場合があります。これは、データを最も適切に表現するものではないかもしれません。

以下に使用できるさまざまなばらつきの指標を示します。

1. 範囲

範囲はデータの最大値と最小値の差です。この情報はデータの2つの側面のみを使用するため、情報量は限られるかもしれません。

範囲はデータの分布についてはあまり多くの情報を提供しないかもしれませんが、データに特定の閾値を使用する場合には、仮説をサポートするのに役立つかもしれません。Pythonを使用してデータの範囲を計算してみましょう。

tips['tip'].max() - tips['tip'].min()

 

9.0

 

2. 分散

 

分散は、データの平均値に基づいてデータのばらつきを示す指標です。各値の平均値からの偏差を2乗し、データの個数で割ることで分散を計算します。通常、データサンプルではなく、データ集団を扱うため、データの個数から1を引きます。サンプル分散の式は以下の画像に示されています。

   

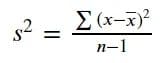
分散は、データが平均値や他のデータからどれだけ離れているかを示す値として解釈することができます。分散が高いほど、データのばらつきが大きいことを意味します。ただし、分散の計算は外れ値に対して敏感です。なぜなら、得点の平均値からの偏差を2乗しているため、外れ値により重みが大きくなるからです。

Pythonを使用してデータの分散を計算してみましょう。

round(tips['tip'].var(),3)

 

1.914

 

上記の分散は、データのばらつきが高いことを示唆していますが、データのばらつきを実際の値で測定するためには標準偏差を使用することができます。

 

3. 標準偏差

 

標準偏差は、データのばらつきを測定する最も一般的な方法であり、分散の平方根を取ることで計算されます。

   

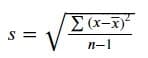
分散と標準偏差の違いは、値が提供する情報にあります。分散値は、値が平均値からどれだけ広がっているかを示すだけであり、分散の単位は元の値と異なるため、元のデータのばらつきを直接測定するためには使用できません。一方、標準偏差の値は元のデータの単位と同じであるため、データのばらつきを直接測定するために使用することができます。

以下のコードで標準偏差を計算してみましょう。

round(tips['tip'].std(),3)

 

1.384

 

標準偏差の最も一般的な応用の1つは、データの間隔を推定することです。経験則または68-95-99.7ルールを使用して、データの間隔を推定することができます。経験則は、データの68%が平均値±1つの標準偏差の範囲にあると推定され、95%が平均値±2つの標準偏差の範囲にあると推定され、99.7%が平均値±3つの標準偏差の範囲にあると推定されます。この範囲外は外れ値と見なすことができます。

 

4. 四分位範囲

 

四分位範囲（IQR）は、第1四分位数と第3四分位数のデータの差を使用して計算されるばらつきの指標です。四分位数自体は、データを4つの異なる部分に分割する値です。より良く理解するために、以下の画像を見てみましょう。

   

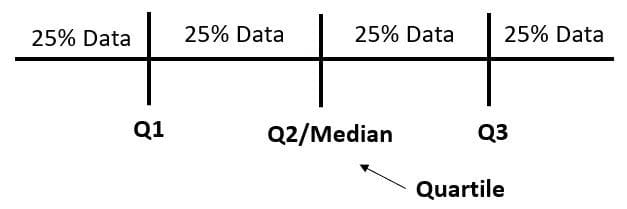
四分位数は、データを分割する値であり、除算の結果ではありません。以下のコードを使用して、四分位数とIQRを見つけることができます。

q1, q3= np.percentile(tips['tip'], [25 ,75])
iqr = q3 - q1

print(f'Q1: {q1}\nQ3: {q3}\nIQR: {iqr}')

 

Q1: 2.0

Q3: 3.5625

IQR: 1.5625

 

NumPyのパーセンタイル関数を使用することで、四分位数を取得することができます。第3四分位数と第1四分位数の差を計算することで、IQRを得ることができます。

IQRは、IQRの値を取り、データの上限/下限を計算することで、データの外れ値を特定するために使用することができます。上限の計算式は、Q3 + 1.5 * IQRであり、下限はQ1 – 1.5 * IQRです。この制限を超える値は、外れ値と見なされます。

より良く理解するために、ボックスプロットを使用してIQRの外れ値検出を理解することができます。

sns.boxplot(tips['tip'])

 

 

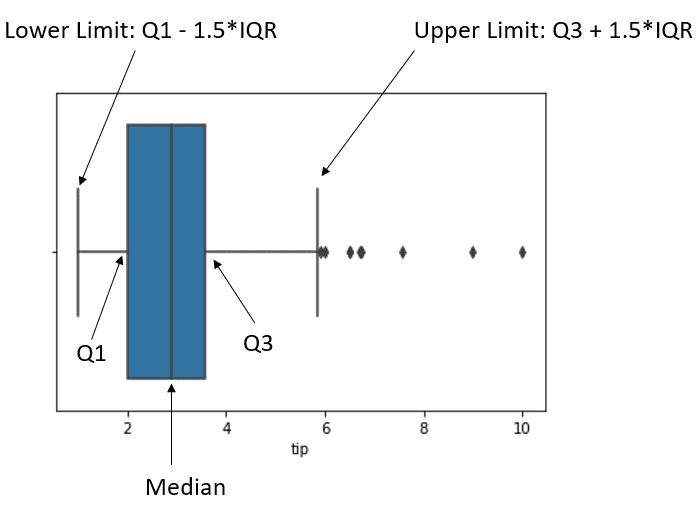
上の画像は、データのボックスプロットとデータの位置を示しています。上限の後の黒い点は、私たちが外れ値と見なすものです。

 

推測統計

 

推測統計は、データサンプルから得られる集団情報を一般化する分野です。推測統計は、全データ集団を取得することができないことが多いため使用され、データサンプルからの推測を行う必要があります。例えば、私たちはインドネシアの人々のAIに対する意見を理解したいとします。しかし、インドネシアの全人口を調査すると時間がかかりすぎます。したがって、人口を代表するサンプルデータを使用して、インドネシアの人々のAIに対する意見について推測します。

さまざまな推測統計を探ってみましょう。

 

1. 標準誤差

 

標準誤差は、サンプル統計量から真の母集団パラメータを推定するための推測統計量です。標準誤差情報は、同じ母集団からのデータサンプルで実験を繰り返した場合、サンプル統計量がどのように変動するかを示します。

平均値の標準誤差（SEM）は、最も一般的に使用される標準誤差のタイプであり、サンプルデータから得られた平均値がどのように母集団を代表するかを示します。SEMを計算するために、以下の方程式を使用します。

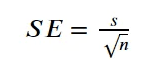  画像提供: 著者 

平均の標準誤差は、計算に標準偏差を使用します。サンプルの数が多いほど、データの標準誤差は小さくなります。つまり、より小さなSEは、サンプルがデータ集団を代表するのに適していることを意味します。

平均の標準誤差を取得するには、以下のコードを使用できます。

from scipy.stats import sem

round(sem(tips['tip']),3)

 

0.089

 

真の母集団平均は、平均±SEMの範囲内に推定されるとよく報告されます。

data_mean = round(tips['tip'].mean(),3)
data_sem = round(sem(tips['tip']),3)
print(f'真の母集団平均は、{data_mean+data_sem}から{data_mean-data_sem}の範囲内に推定されます。')

 

真の母集団平均は、範囲3.087〜2.9090000000000003の間に推定される

 

2. 信頼区間

 

信頼区間は、真の母集団パラメータを推定するために使用されますが、信頼レベルを導入します。信頼レベルは、一定の信頼度で真の母集団パラメータの範囲を推定します。

統計学では、信頼は確率として記述することができます。たとえば、信頼レベルが90％の信頼区間では、真の平均母集団推定値が信頼区間の上限値と下限値の間にある確率は100回中90回です。CIは以下の式で計算されます。

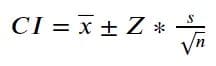  画像提供：著者 

上記の式は、Z以外は馴染みのある表記です。Zは、信頼レベル（たとえば95％）を定義し、z-クリティカル値表を使用してz-スコア（信頼レベル95％の場合は1.96）を決定することで取得されるz-スコアです。また、サンプルが小さい場合や30未満の場合は、t-分布表を使用する必要があります。

以下のコードを使用してPythonでCIを取得できます。

import scipy.stats as st

st.norm.interval(confidence=0.95, loc=data_mean, scale=data_sem)

 

(2.8246682963727068, 3.171889080676473)

 

上記の結果は、データの真の母集団平均が95％の信頼レベルで範囲2.82〜3.17の間にあることを示しています。

 

3. 仮説検定

 

仮説検定は、データサンプルから母集団について結論を導くための推測統計学の手法です。推定される母集団は、母集団パラメータまたは確率である可能性があります。

仮説検定では、帰無仮説（H0）と対立仮説（Ha）という仮定を持つ必要があります。帰無仮説と対立仮説は常に互いに反対です。仮説検定手順は、サンプルデータを使用して帰無仮説を棄却できるかどうか、または帰無仮説を棄却できないか（つまり対立仮説を受け入れること）を決定します。

帰無仮説を棄却するために仮説検定手法を実行する場合、有意水準を決定する必要があります。有意水準は、テストで許容されるタイプ1エラー（H0が真の場合にH0を棄却する）の最大確率です。通常、有意水準は0.05または0.01です。

サンプルから結論を導くために、仮説検定は帰無仮説が真であると仮定した場合にサンプル結果がどれだけ可能性があるかを測定するためにP値を使用します。P値が有意水準より小さい場合、帰無仮説を棄却します。そうでなければ、棄却できません。

仮説検定は、任意の母集団パラメータで実行できる手法であり、複数のパラメータでも実行できます。たとえば、以下のコードは2つの異なる母集団間でt検定を実行し、このデータが他のデータと有意に異なるかどうかを確認します。

st.ttest_ind(tips[tips['sex'] == 'Male']['tip'], tips[tips['sex'] == 'Female']['tip'])

 

Ttest_indResult(statistic=1.387859705421269, pvalue=0.16645623503456755)

 

t検定では、2つのグループ間の平均値を比較します（ペアワイズテスト）。t検定の帰無仮説は、2つのグループの平均値に差がないということであり、対立仮説は2つのグループの平均値に差があるということです。

t検定の結果、男性と女性のチップは有意に異ならないことが示されます。なぜなら、P値が0.05の有意水準を上回っているためです。つまり、帰無仮説を棄却できず、2つのグループの平均値には差がないと結論付けられます。

もちろん、上記のテストは仮説検定の例を簡略化したものです。仮説検定を実行する際に知る必要がある前提条件や、ニーズに応じて実行できる多くのテストがあります。

 

結論

 

統計学のフィールドには、知っておく必要のある2つの主要な分野があります：記述統計学と推測統計学です。記述統計学はデータの要約に関心を持ちますが、推測統計学は人口についての推論を行うためにデータの一般化に取り組みます。この記事では、Pythonコードを使用した具体例を交えながら、記述統計学と推測統計学について説明しました。コーネリウス・ユダ・ウィジャヤはデータサイエンスアシスタントマネージャー兼データライターです。オールリアンツ・インドネシアでフルタイムで働きながら、彼はソーシャルメディアと執筆メディアを通じてPythonとデータのヒントを共有することが大好きです。 

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!