「トランスフォーマーを用いたジャズコードの解析」
Analyzing Jazz Chords with Transformers
ツリーベースの音楽分析におけるデータ駆動型アプローチ

この記事では、「グラフベースのニューラルデコーダを用いたジャズコードシーケンスの予測」という研究論文の一部をまとめます。この論文では、音楽のツリー構造を解析するためのデータ駆動型システムを提案しています。
この研究は、音楽データに対して唯一の選択肢である文法ベースの解析システムに対する私の不満から動機づけられています。以下はその不満です:
- 文法の構築には多くのドメイン知識が必要です
- 未知の構成やノイズのあるデータの場合、パーサは失敗します
- 複数の音楽的要素を単一の文法ルールで考慮するのは難しいです
- 開発をサポートするPythonフレームワークがないため、開発に困難を伴います
私のアプローチ(自然言語処理の類似した研究に触発されて)は、文法に依存せず、ノイズのある入力に対して部分的な結果を生成する、複数の音楽的要素を容易に取り扱う、そしてPyTorchで実装されているという特徴があります。
もしも解析や文法に詳しくない場合、または知識を振り返りたい場合は、少し戻って説明します。
「パース(解析)」とは何ですか?
パースとは、数列の要素を葉とする数学的な構造(ツリー)を予測/推論することを指します。

では、なぜツリーが必要なのでしょうか?
以下は、ジャズコードのシーケンス(「Take the A Train」のセクションA)です。

ジャズ音楽では、コード同士は知覚的な関係の複雑なシステムによって結びついています。例えば、Dm7はG7の準備となります。つまり、Dm7はG7よりも重要ではなく、別の再編成では省略される可能性があります。同様に、D7は補助的なドミナント(ドミナントのドミナント)であり、またG7を指しています。
このような和音の関係をツリーで表現し、音楽の分析やリハーモナイズなどのタスクに役立てることができます。ただし、音楽の和音は主にシーケンスとして利用可能なため、自動的にそのようなツリー構造を構築できるシステムが必要です。
構成ツリーと依存ツリー
続ける前に、2種類のツリーを区別する必要があります。
音楽学者は通常、構成ツリーと呼ばれるものを使用します。以下の画像で確認できます。構成ツリーには、葉(青色のコード – 入力シーケンスの要素)と内部ノード(オレンジ色のコード – 子の葉の簡略化)が含まれています。

この研究では、代わりに依存ツリーと呼ばれる別の種類のツリーを考慮します。この種のツリーには内部ノードはなく、シーケンスの要素を接続する有向弧のみが存在します。

構成ツリーから依存ツリーを生成することも可能であり、後述するアルゴリズムで行うことができます。
データセット
このデータ駆動型アプローチでは、訓練およびテストに使用するコードシーケンス(入力データ)とツリー(正解データ)のデータセットが必要です。Jazz Treebank¹を使用します。このデータセットはGitHubリポジトリで公開されており(非営利目的のアプリケーションに無料で使用できます)、この記事で使用するための著者の許可を取得しました。具体的には、すべてのコードと注釈が含まれたJSONファイルが提供されています。
私たちのシステムでは、入力の各コードについて、3つの特徴をモデル化しています:
- ルートは[0..11]の整数で、C -> 0、C# -> 1などです。
- 基本形は[0..5]の整数で、major、minor、augmented、half-diminished、diminished、suspended (sus) の中から選択されます。
- 拡張は[0,1,2]の整数で、6、minor 7、または major 7 の中から選択されます。
コードの特徴をコードラベル(文字列)から生成するために、次のような正規表現を使用することができます(このコードはこのデータセットに対して動作するため、他のコードデータセットでは形式が異なる場合があります)。
def parse_chord_label(chord_label): # コード記号の正規表現パターンを定義
pattern = r"([A-G][#b]?)(m|\+|%|o|sus)?(6|7|\^7)?" # パターンを入力のコードにマッチさせる
match = re.match(pattern, chord_label)
if match:
# マッチオブジェクトからルート、基本コード形式、拡張を抽出する
root = match.group(1)
form = match.group(2) or "M"
ext = match.group(3) or ""
return root, form, ext
else:
# 入力が有効なコード記号でない場合は None を返す
raise ValueError("Invalid chord symbol: {}".format(chord_label))最後に、依存木を生成する必要があります。JHTデータセットには構成木のみが含まれており、ネストされた辞書としてエンコードされています。これを依存木に変換するために、再帰関数を使用します。関数のメカニズムは次のように説明できます。
完全な構成木と依存関係のない依存木(シーケンス要素のみでラベル付けされたノードのみで構成される)から開始します。アルゴリズムは、各グループの主要な子とすべてのセカンダリ子関係を使用して、グループラベルとセカンダリ子ラベルの間に依存関係アークを作成します。
def parse_jht_to_dep_tree(jht_dict):
"""Pythonのジャズハーモニーツリーディクショナリを依存関係のリストと葉のコードのリストに解析する。"""
all_leaves = []
def _iterative_parse_jht(dict_elem):
"""Pythonのジャズハーモニーツリーディクショナリを依存関係のリストに解析するための反復関数。"""
children = dict_elem["children"]
if children == []: # 再帰終了条件
out = (
[],
{"index": len(all_leaves), "label": dict_elem["label"]},
)
# 現在のノードのラベルをグローバルな葉のリストに追加する
all_leaves.append(dict_elem["label"])
return out
else: # 再帰呼び出し
assert len(children) == 2
current_label = noast(dict_elem["label"])
out_list = [] # 依存関係のリスト
iterative_result_left = _iterative_parse_jht(children[0])
iterative_result_right = _iterative_parse_jht(children[1])
# より深く計算された依存関係リストをマージする
out_list.extend(iterative_result_left[0])
out_list.extend(iterative_result_right[0])
# ラベルが左の子または右の子に対応するかどうかをチェックし、対応する結果を返す
if iterative_result_right[1]["label"] == current_label: # 両方の子が等しい場合のデフォルトは左右アーチに進む
# 現在のノードの依存関係を追加する
out_list.append((iterative_result_right[1]["index"], iterative_result_left[1]["index"]))
return out_list, iterative_result_right[1]
elif iterative_result_left[1]["label"] == current_label:
# print("right-left arc on label", current_label)
# 現在のノードの依存関係を追加する
out_list.append((iterative_result_left[1]["index"], iterative_result_right[1]["index"]))
return out_list, iterative_result_left[1]
else:
raise ValueError("Something went wrong with label", current_label)
dep_arcs, root = _iterative_parse_jht(jht_dict)
dep_arcs.append((-1,root["index"])) # ルートへの接続を追加、インデックスは-1
# ルートへの自己ループを追加
dep_arcs.append((-1,-1)) # ルートへのループ接続を追加、インデックスは-1
return dep_arcs, all_leaves依存解析モデル
私たちの解析モデルの仕組みは非常にシンプルです:すべての可能なアークを考慮し、アークの予測子(単純な2値分類器)を使用して、そのアークがツリーの一部であるかどうかを予測します。
ただし、2つのコードだけでこの選択をするのはかなり難しいです。コンテキストが必要です。このようなコンテキストは、トランスフォーマーエンコーダーで構築されます。
要約すると、パーシングモデルは2つのステップで動作します:
- 入力シーケンスはトランスフォーマーエンコーダーを通過して、文脈情報を豊かにします。
- バイナリクラシファイアは、すべての可能な依存アークのグラフを評価し、不要なアークをフィルタリングします。
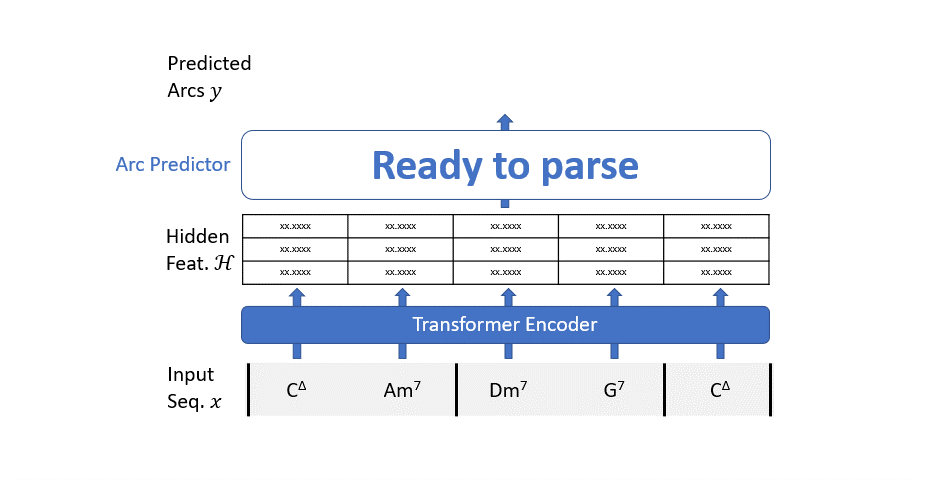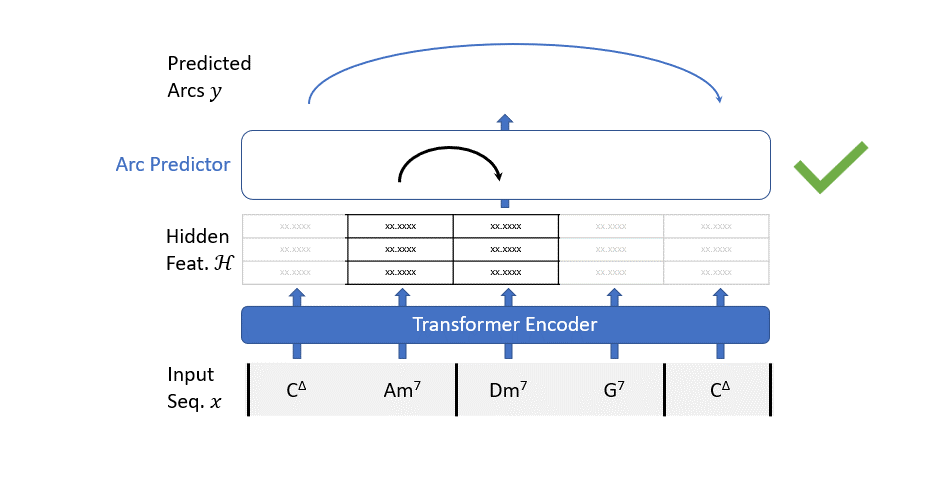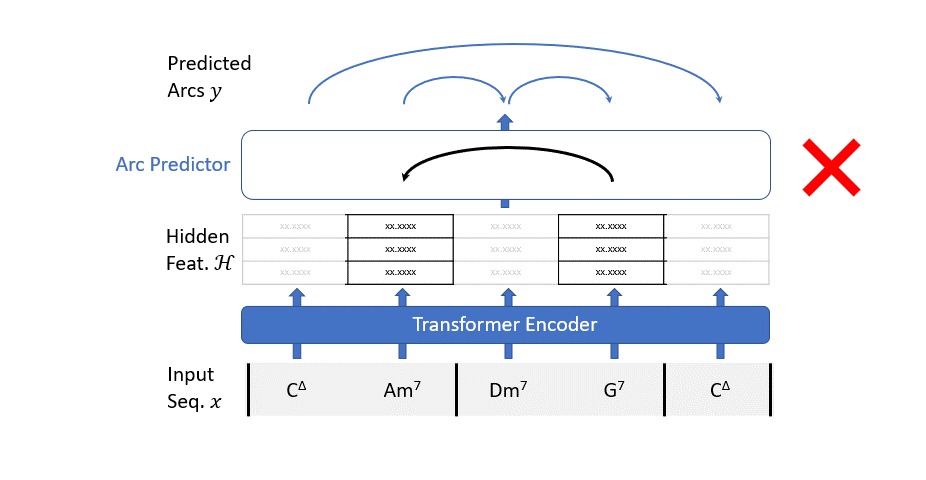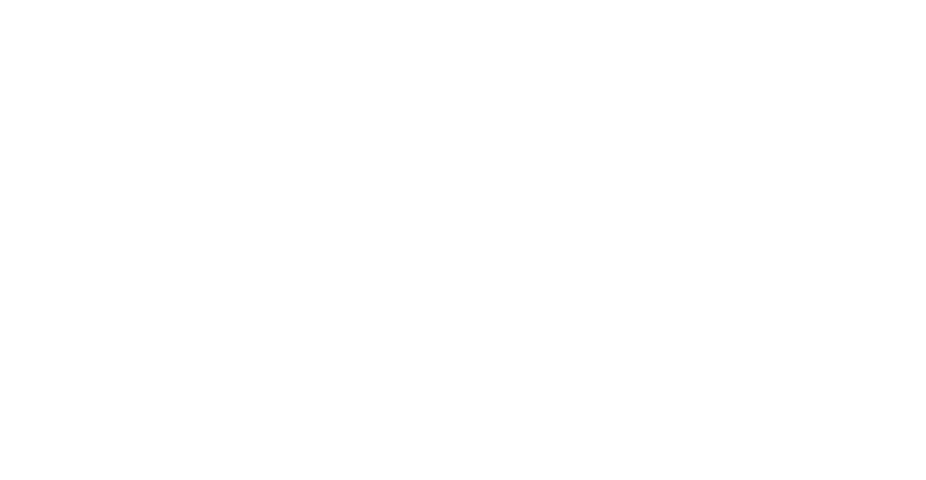
トランスフォーマーエンコーダーは標準のアーキテクチャに従います。各カテゴリカルな入力特徴を連続的な多次元空間の点にマッピングするために学習可能な埋め込みレイヤーを使用します。すべての埋め込みは合計されるため、各特徴に使用する次元をネットワークが「決定する」ことができます。
import torch.nn as nnclass TransformerEncoder(nn.Module): def __init__( self, input_dim, hidden_dim, encoder_depth, n_heads = 4, dropout=0, embedding_dim = 8, activation = "gelu", ): super().__init__() self.input_dim = input_dim self.positional_encoder = PositionalEncoding( d_model=input_dim, dropout=dropout, max_len=200 ) encoder_layer = nn.TransformerEncoderLayer(d_model=input_dim, dim_feedforward=hidden_dim, nhead=n_heads, dropout =dropout, activation=activation) encoder_norm = nn.LayerNorm(input_dim) self.transformer_encoder = nn.TransformerEncoder(encoder_layer, num_layers=encoder_depth, norm=encoder_norm) self.embeddings = nn.ModuleDict({ "root": nn.Embedding(12, embedding_dim), "form": nn.Embedding(len(CHORD_FORM), embedding_dim), "ext": nn.Embedding(len(CHORD_EXTENSION), embedding_dim), "duration": nn.Embedding(len(JTB_DURATION), embedding_dim, "metrical": nn.Embedding(METRICAL_LEVELS, embedding_dim) }) def forward(self, sequence): root = sequence[:,0] form = sequence[:,1] ext = sequence[:,2] duration = sequence[:,3] metrical = sequence[:,4] # カテゴリカル特徴を埋め込みに変換 root = self.embeddings["root"](root.long()) form = self.embeddings["form"](form.long()) ext = self.embeddings["ext"](ext.long()) duration = self.embeddings["duration"](duration.long()) metrical = self.embeddings["metrical"](metrical.long()) # すべての埋め込みを合計 z = root + form + ext + duration + metrical # 位置エンコーディングを追加 z = self.positional_encoder(z) # 形状を変更 (seq_len, batch = 1, input_dim) z = torch.unsqueeze(z,dim= 1) # トランスフォーマーエンコーダーを実行 z = self.transformer_encoder(src=z, mask=src_mask) # バッチ次元を削除 z = torch.squeeze(z, dim=1) return z, ""class PositionalEncoding(nn.Module): def __init__(self, d_model: int, dropout: float = 0.1, max_len: int = 500): super().__init__() self.dropout = nn.Dropout(p=dropout) position = torch.arange(max_len).unsqueeze(1) div_term = torch.exp(torch.arange(0, d_model, 2) * (-np.log(10000.0) / d_model)) pe = torch.zeros(max_len, d_model) pe[:, 0::2] = torch.sin(position * div_term) pe[:, 1::2] = torch.cos(position * div_term) self.register_buffer('pe', pe) def forward(self, x: torch.Tensor) -> torch.Tensor: x = x + self.pe[:x.size(0)] return self.dropout(x)アーク予測器は、2つのコードの隠れた特徴の連結を入力とする線形層です。行列の乗算の力により、すべてのアークの分類ステップが並列で行われます。
class ArcPredictor(nn.Module): def __init__(self, hidden_channels, activation=F.gelu, dropout=0.3): super().__init__() self.activation = activation self.root_linear = nn.Linear(1, hidden_channels) # rootの特徴量を生成するための線形層 self.lin1 = nn.Linear(2*hidden_channels, hidden_channels) self.lin2 = nn.Linear(hidden_channels, 1) self.dropout = nn.Dropout(dropout) self.norm = nn.LayerNorm(hidden_channels) def forward(self, z, pot_arcs): # root要素のための列を追加 root_feat = self.root_linear(torch.ones((1,1), device=z.device)) z = torch.vstack((root_feat,z)) # 計算を進める z = self.norm(z) # 2つのノードの埋め込みを連結、形状は (num_pot_arcs, 2*hidden_channels) z = torch.cat([z[pot_arcs[:, 0]], z[pot_arcs[:, 1]]], dim=-1) # 線形層を通過、形状は (num_pot_arcs, hidden_channels) z = self.lin1(z) # 活性化関数を通過、形状は (num_pot_arcs, hidden_channels) z = self.activation(z) # 正規化 z = self.norm(z) # ドロップアウト z = self.dropout(z) # さらに線形層を通過、形状は (num_pot_arcs, 1) z = self.lin2(z) # 形状が (num_pot_arcs,) のベクトルを返す return z.view(-1)トランスフォーマーエンコーダーとアーク予測器を1つのtorchモジュールに配置して、使用を簡素化できます。
class ChordParser(nn.Module): def __init__(self, input_dim, hidden_dim, num_layers, dropout=0.2, embedding_dim = 8, use_embedding = True, n_heads = 4): super().__init__() self.activation = nn.functional.gelu # エンコーダーを初期化します self.encoder = NotesEncoder(input_dim, hidden_dim, num_layers, dropout, embedding_dim, n_heads=n_heads) # デコーダーを初期化します self.decoder = ArcDecoder(input_dim, dropout=dropout) def forward(self, note_features, pot_arcs, mask=None): z = self.encoder(note_features) return self.decoder(z, pot_arcs)損失関数
損失関数として、2つの損失の合計を使用しています:
- バイナリクロスエントロピー損失:問題をバイナリ分類問題と見なし、各アークが予測されるかどうかを判断します。
- クロスエントロピー損失:問題をマルチクラス分類問題と見なし、ヘッド→従属アークの中で正しい従属アークを予測する必要があります。
loss_bce = torch.nn.BCEWithLogitsLoss()loss_ce = torch.nn.CrossEntropyLoss(ignore_index=-1)total_loss = loss_bce + loss_ce後処理
まだ解決しなければならない問題が1つあります。トレーニング中に予測されたアークがツリー構造を形成する必要があるという事実は、いかなる時点でも強制されていません。したがって、アークループなどの無効な構成が発生する可能性があります。幸いなことに、これを防止するために使用できるアルゴリズムがあります:アイズナーのアルゴリズム。²
予測された確率が0.5よりも大きい場合にのみアークが存在すると仮定する代わりに、すべての予測を保存し、サイズが(コードの数、コードの数)の正方行列(隣接行列)に実行します。
# https://github.com/HMJW/biaffine-parserからの変更def eisner(scores, return_probs = False): """アイズナーのアルゴリズムを使用して解析します。 マトリックスは次の規則に従います: scores[i][j] = p(i=head, j=dep) = p(i --> j) """ rows, collumns = scores.shape assert rows == collumns, 'scores matrix must be square' num_words = rows - 1 # 単語数(ルートを除く)。 # CKYテーブルを初期化します。 complete = np.zeros([num_words+1, num_words+1, 2]) # s、t、direction(right=1)。 incomplete = np.zeros([num_words+1, num_words+1, 2]) # s、t、direction(right=1)。 complete_backtrack = -np.ones([num_words+1, num_words+1, 2], dtype=int) # s、t、direction(right=1)。 incomplete_backtrack = -np.ones([num_words+1, num_words+1, 2], dtype=int) # s、t、direction(right=1)。 incomplete[0, :, 0] -= np.inf # より小さいアイテムからより大きいアイテムへのループ。 for k in range(1, num_words+1): for s in range(num_words-k+1): t = s + k # 最初に不完全なアイテムを作成します。 # 左の木 incomplete_vals0 = complete[s, s:t, 1] + complete[(s+1):(t+1), t, 0] + scores[t, s] incomplete[s, t, 0] = np.max(incomplete_vals0) incomplete_backtrack[s, t, 0] = s + np.argmax(incomplete_vals0) # 右の木 incomplete_vals1 = complete[s, s:t, 1] + complete[(s+1):(t+1), t, 0] + scores[s, t] incomplete[s, t, 1] = np.max(incomplete_vals1) incomplete_backtrack[s, t, 1] = s + np.argmax(incomplete_vals1) # 次に完全なアイテムを作成します。 # 左の木 complete_vals0 = complete[s, s:t, 0] + incomplete[s:t, t, 0] complete[s, t, 0] = np.max(complete_vals0) complete_backtrack[s, t, 0] = s + np.argmax(complete_vals0) # 右の木 complete_vals1 = incomplete[s, (s+1):(t+1), 1] + complete[(s+1):(t+1), t, 1] complete[s, t, 1] = np.max(complete_vals1) complete_backtrack[s, t, 1] = s + 1 + np.argmax(complete_vals1) value = complete[0][num_words][1] heads = -np.ones(num_words + 1, dtype=int) backtrack_eisner(incomplete_backtrack, complete_backtrack, 0, num_words, 1, 1, heads) value_proj = 0.0 for m in range(1, num_words+1): h = heads[m] value_proj += scores[h, m] if return_probs: return heads, value_proj else: return headsdef backtrack_eisner(incomplete_backtrack, complete_backtrack, s, t, direction, complete, heads): """ アイズナーのアルゴリズムのバックトラッキングステップ。 - incomplete_backtrackは、開始位置、終了位置、および方向フラグ(0は左、1は右を意味する)でインデックス付けされた(NW+1)×(NW+1)のnumpy配列です。この配列には、不完全スパンを構築するアイズナーアルゴリズムの各ステップのarg-maxが含まれています。 - complete_backtrackは、開始位置、終了位置、および方向フラグ(0は左、1は右を意味する)でインデックス付けされた(NW+1)×(NW+1)のnumpy配列です。この配列には、完全なスパンを構築するアイズナーアルゴリズムの各ステップのarg-maxが含まれています。 - sは現在のスパンの開始です - tは現在のスパンの終了です - directionは0(左のアタッチメント)または1(右のアタッチメント)です - completeは現在のスパンが完全である場合は1、それ以外の場合は0です - headsは、各単語のヘッドを格納するための(NW+1)サイズの整数のnumpy配列です。 """ if s == t: return if complete: r = complete_backtrack[s][t][direction] if direction == 0: backtrack_eisner(incomplete_backtrack, complete_backtrack, s, r, 0, 1, heads) backtrack_eisner(incomplete_backtrack, complete_backtrack, r, t, 0, 0, heads) return else: backtrack_eisner(incomplete_backtrack, complete_backtrack, s, r, 1, 0, heads) backtrack_eisner(incomplete_backtrack, complete_backtrack, r, t, 1, 1, heads) return else: r = incomplete_backtrack[s][t][direction] if direction == 0: heads[s] = t backtrack_eisner(incomplete_backtrack, complete_backtrack, s, r, 1, 1, heads) backtrack_eisner(incomplete_backtrack, complete_backtrack, r+1, t, 0, 1, heads) return else: heads[t] = s backtrack_eisner(incomplete_backtrack, complete_backtrack, s, r, 1, 1, heads) backtrack_eisner(incomplete_backtrack, complete_backtrack, r+1, t, 0, 1, heads) return結論
私は和音の依存解析のためのシステムを提案しました。このシステムでは、トランスフォーマーを使用して和音の文脈に基づく隠れた表現を構築し、分類器を使用して2つの和音がアークで接続されるべきかどうかを選択します。
競合するシステムと比較しての主な利点は、このアプローチが特定の象徴的な文法に依存しないことです。したがって、複数の音楽的特徴を同時に考慮することができ、連続した文脈情報を利用することができ、ノイズのある入力に対して部分的な結果を出力することができます。
この記事を適切なサイズに保つため、説明とコードはシステムの最も興味深い部分に焦点を当てています。より詳しい説明はこの科学的な論文で見つけることができ、すべてのコードはこのGitHubリポジトリで見つけることができます。
(すべての画像は筆者によるものです。)
参考文献
- D. Harasim, C. Finkensiep, P. Ericson, T. J. O’Donnell, and M. Rohrmeier, “The jazz harmony treebank,” in Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), 2020, pp. 207–215.
- J. M. Eisner, “Three new probabilistic models for dependency parsing: An exploration,” in Proceedings of the International Conference on Computational Linguistics (COLING), 1996.
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
- シンガポール国立大学の研究者が提案するMind-Video:脳のfMRIデータを使用してビデオイメージを再現する新しいAIツール
- UTオースティンとUCバークレーの研究者が、アンビエントディフュージョンを紹介します:入力としての破損したデータのみを使用してディフュージョンモデルをトレーニング/微調整するためのAIフレームワーク
- 「LLMsを使用したモバイルアプリの音声と自然言語の入力」
- CDPとAIの交差点:人工知能が顧客データプラットフォームを革新する方法
- LangChainによるAIの変革:テキストデータのゲームチェンジャー
- 最適なテクノロジー/ベンダーを選ぶための体系的なアプローチ:MLOpsバージョン
- 「Pythonを使った合成データの生成」
