「言語モデルにアルゴリズム的な推論を教える」
Algorithmic inference in language models
Posted by Hattie Zhou, MILAの大学院生、Hanie Sedghi, Googleの研究科学者
GPT-3やPaLMなどの大規模言語モデル(LLM)は、モデルとトレーニングデータのサイズを拡大することで、近年驚異的な進歩を遂げています。それにもかかわらず、LLMが象徴的に推論できるか(すなわち、論理的なルールに基づいて記号を操作できるか)という長年の議論がありました。たとえば、LLMは、数字が小さい場合には簡単な算術演算を実行できますが、数字が大きい場合は苦労します。これは、LLMがこれらの算術演算を実行するために必要な基本的なルールを学習していないことを示唆しています。
ニューラルネットワークはパターンマッチング能力に優れていますが、データ中の偶発的な統計的パターンに過学習しやすいです。これは、トレーニングデータが大きく多様であり、評価が分布内である場合には良いパフォーマンスに影響しません。ただし、加算などのルールベースの推論を必要とするタスクでは、LLMは分布外の一般化に苦労し、トレーニングデータの偶発的な相関は真のルールベースの解決策よりもはるかに容易に利用されることがしばしばあります。その結果、さまざまな自然言語処理タスクでの重要な進展にもかかわらず、加算などの簡単な算術タスクのパフォーマンスは依然として課題のままです。MATHデータセットでのGPT-4のささやかな改善にもかかわらず、エラーは主に算術と計算のミスによるものです。したがって、重要な問題は、LLMがアルゴリズム的な推論が可能かどうかということです。アルゴリズム的な推論は、アルゴリズムを定義する一連の抽象的なルールを適用してタスクを解決することを含みます。
「コンテキスト学習を通じたアルゴリズム的な推論の教育」では、コンテキスト学習を活用してLLMにアルゴリズム的な推論能力を可能にするアプローチについて説明しています。コンテキスト学習とは、モデルがモデルのコンテキスト内でそれに関するいくつかの例を見た後にタスクを実行できる能力を指します。タスクはプロンプトを使用してモデルに指定され、重みの更新は必要ありません。また、より困難な算術問題においてプロンプトで見られるものよりも強力な一般化を実現するための革新的なアルゴリズム的プロンプティング技術を提案しています。最後に、適切なプロンプト戦略を選択することで、モデルが分布外の例でアルゴリズムを信頼性を持って実行できることを示しています。
 |
| アルゴリズム的プロンプトを提供することで、コンテキスト学習を通じてモデルに算術のルールを教えることができます。この例では、LLM(単語予測)は、簡単な加算の質問(例:267 + 197)をプロンプトとして入力すると正しい答えを出力しますが、桁数の長い類似の加算の質問に対しては失敗します。ただし、より困難な質問に加算のアルゴリズム的プロンプトを追加すると(単語予測の下に表示される青いボックスと白い+)、モデルは正しく答えることができます。さらに、モデルは一連の加算計算を合成することによって乗算アルゴリズム( X )をシミュレートすることができます。 |
アルゴリズムをスキルとして教える
モデルにアルゴリズムをスキルとして教えるために、アルゴリズムプロンプトを開発します。これは、他の根拠に基づいたアプローチ(スクラッチパッドや思考の連鎖など)を基に構築されます。アルゴリズムプロンプトは、LLMからアルゴリズム的な推論能力を抽出し、他のプロンプトアプローチと比較して2つの注目すべき特徴があります。 1)アルゴリズミックな解決策に必要な手順を出力してタスクを解決し、2)LLMによる誤解釈の余地がないように、各アルゴリズミックな手順を十分な詳細で説明します。
アルゴリズム的なプロンプトの直感を得るために、2つの数字の加算のタスクを考えてみましょう。スクラッチパッドスタイルのプロンプトでは、右から左に各桁を処理し、各ステップでキャリー値(現在の桁が9より大きい場合は次の桁に1を追加します)を追跡します。ただし、キャリーのルールはキャリー値の数例を見た後ではあいまいです。キャリーのルールを明示するために明示的な方程式を含めると、モデルは関連する詳細に焦点を当て、プロンプトをより正確に解釈することができることがわかります。この洞察を活用して、2つの数字の加算のためのアルゴリズム的なプロンプトを開発しました。計算の各ステップに対して明示的な方程式を提供し、曖昧さのない形式でさまざまなインデックス操作を説明します。
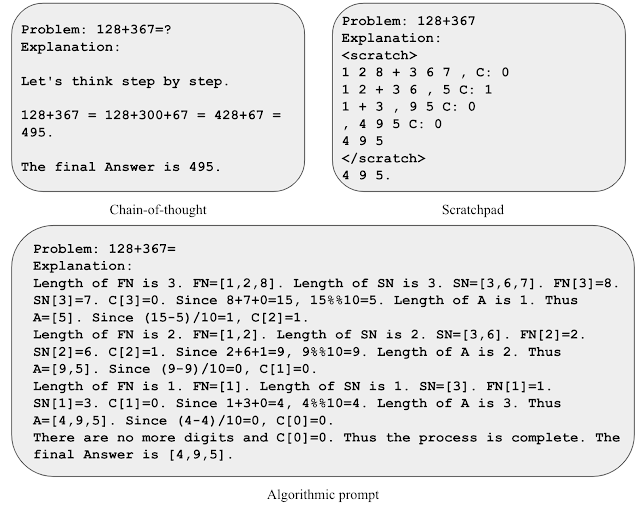 |
| さまざまな加算のプロンプト戦略のイラスト。 |
答えの桁数が最大5桁までの加算のプロンプト例を3つだけ使用して、19桁までの加算のパフォーマンスを評価します。正確性は、答えの長さに均等にサンプリングされた合計2,000の例において測定されます。以下に示すように、アルゴリズムのプロンプトの使用により、プロンプトで見られる以上に長い質問に対しても高い正確性が維持されており、モデルが入力に関係ないアルゴリズムを実行することによってタスクを解決していることが示されています。
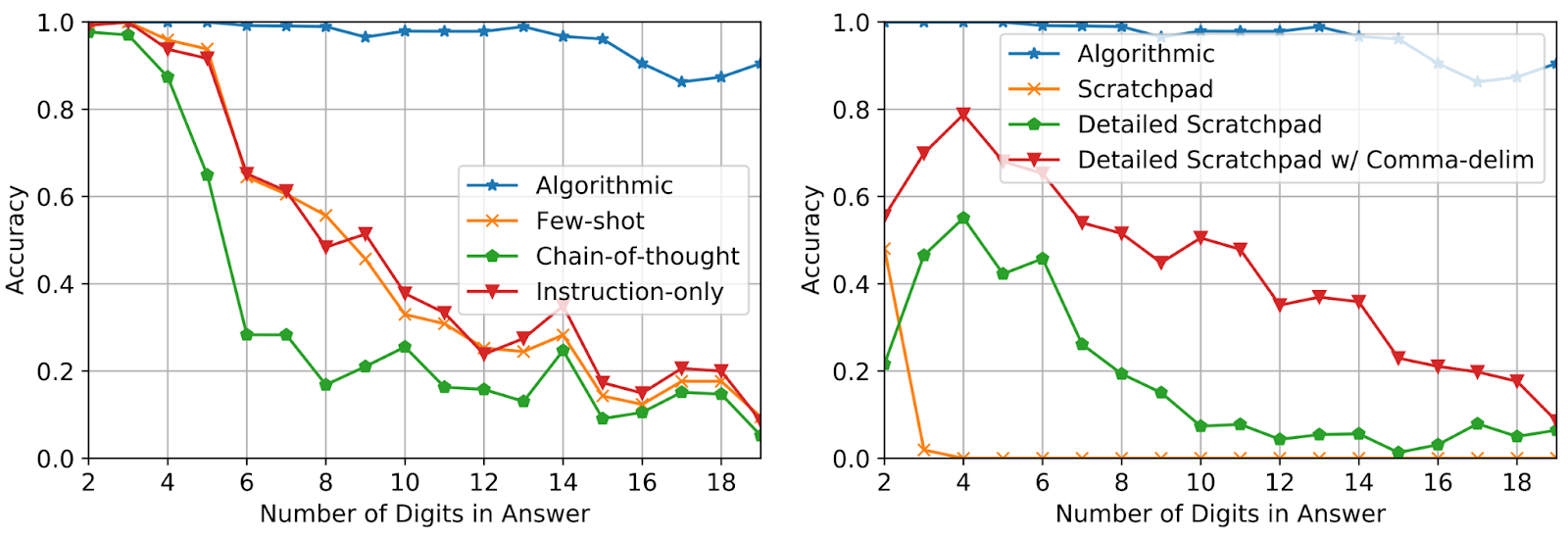 |
| 異なるプロンプトのメソッドによる加算問題のテスト正確性の長さの増加。 |
アルゴリズム的なスキルを道具として活用する
モデルがより一般的な推論プロセスにおいてアルゴリズミックな推論を活用できるかどうかを評価するために、学校の数学のワードプロブレム(GSM8k)を使用してパフォーマンスを評価します。具体的には、GSM8kからの加算計算をアルゴリズミックな解決策で置き換える試みを行います。
コンテキストの長さの制限と異なるアルゴリズム間の干渉の可能性に基づき、複雑なタスクを解決するために異なるプロンプトのモデル同士が相互作用する戦略を探求します。GSM8kの文脈では、考えの連鎖のプロンプトを使用した非公式な数学的推論を専門とするモデルと、アルゴリズム的なプロンプトを使用した加算を専門とする2つ目のモデルがあります。非公式な数学的推論モデルは、アリスメティックの手順を実行するために特化したトークンを出力するようにプロンプトされ、クエリをトークン間で抽出し、加算モデルに送信し、答えを最初のモデルに返します。その後、最初のモデルは出力を続けます。GSM8kの難しい問題(GSM8k-Hard)を使用してアプローチを評価し、加算のみの質問をランダムに50個選択し、質問の数値を増やします。
 |
| GSM8k-Hardデータセットからの例。アルゴリズミックな呼び出しが行われるべき時にブラケットで示された考えの連鎖プロンプトが補完されています。 |
私たちは、GSM8k-Hardに取り組むために、専門的なプロンプトを使用した個別のコンテキストとモデルを使用することが効果的な方法であることがわかりました。以下では、アルゴリズム的な呼び出しを行うモデルのパフォーマンスが、思考の連鎖のベースラインの2.3倍であることを確認します。最後に、この戦略は、異なるスキルに特化したLLMs間の相互作用を促進することにより、複雑なタスクを解決する例です。
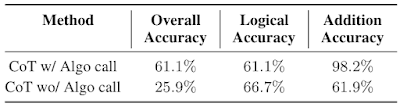 |
| アルゴリズム的な呼び出しの有無でのGSM8k-Hardにおける連鎖思考(CoT)のパフォーマンス。 |
結論
私たちは、コンテキスト内の学習と新しいアルゴリズムのプロンプティング技術を活用して、LLMs内のアルゴリズム的な推論能力を引き出すアプローチを提案します。私たちの結果は、より詳細な説明を提供することで、より長いコンテキストをより優れた推論パフォーマンスに変換することが可能かもしれないことを示唆しています。したがって、これらの結果は、長いコンテキストを使用したり、より情報量の多い根拠を生成したりする能力が有望な研究方向であることを指摘しています。
謝辞
この論文への貴重な貢献とブログへの素晴らしいフィードバックに対して、共著者のBehnam Neyshabur、Azade Nova、Hugo Larochelle、およびAaron Courvilleに感謝します。また、この投稿でのアニメーションの作成には、Tom Smallさんに感謝します。この作業は、Hattie ZhouさんのGoogle Researchでのインターンシップ中に行われました。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles