「モンテカルロシミュレーションを通じてA/Bテストのパフォーマンスを理解するための初心者向けガイド」

A beginner's guide to understanding the performance of A/B testing through Monte Carlo simulations

このチュートリアルでは、共変量がランダム化実験におけるA/Bテストの精度にどのように影響するかを探求します。適切にランダム化されたA/Bテストでは、治療群と対照群の平均結果を比較することによってリフトを計算します。ただし、治療以外の要素が結果に与える影響は、A/Bテストの統計的特性を決定します。たとえば、テストのリフト計算で影響力のある要素を省略すると、サンプルサイズが増加するにつれて真の値に収束するとしても、リフトの推定値が非常に不正確になる場合があります。

RMSE、バイアス、およびテストのサイズについて学び、シミュレートされたデータを生成しモンテカルロ実験を実行することによってA/Bテストのパフォーマンスを理解します。このような作業は、データ生成プロセス（DGP）の特性がA/Bテストのパフォーマンスにどのように影響するかを理解するのに役立ち、実世界のデータに対してA/Bテストを実行する際にも役立ちます。まず、推定量のいくつかの基本的な統計的特性について説明します。

推定量の統計的特性

平均二乗誤差（RMSE）

平均二乗誤差（Root Mean Square Error：RMSE）は、モデルまたは推定量によって予測された値と観測された値の間の差を頻繁に使用される尺度です。これは予測と実際の観測値の平均二乗差の平方根です。RMSEの式は次の通りです：

RMSE = sqrt[(1/n) * Σ(actual – prediction)²]

• 「Langchain Agentsを使用して、独自のデータアナリストアシスタントを作成しましょう」
• 知識グラフ：AIとデータサイエンスのゲームチェンジャー
• 大学フットボールカンファレンスの再編成 – Pythonにおける探索的データ分析

RMSEは、大きな誤差に対して相対的に高い重みを与えるため、大きな誤差が望ましくない場合により有用です。

バイアス

統計学において、推定量のバイアスとは、この推定量の期待値と推定されたパラメータの真の値との差です。バイアスがゼロの推定量または意思決定ルールはバイアスがないと言われます。つまり、アルゴリズムが一貫して同じ間違った結果を学習することによって正確な基礎となる関係を見逃す場合にバイアスが発生します。

たとえば、家の特徴に基づいて家の価格を予測しようとしており、予測が常に実際の価格よりも10万ドル低い場合、モデルにはバイアスがあります。

サイズ

統計学における仮説検定における「テストのサイズ」とは、テストの有意水準を指します。ギリシャ文字のα（アルファ）で表されることが多いです。有意水準またはテストのサイズは、帰無仮説を棄却するためにテスト統計量が超えなければならないしきい値です。

実際には帰無仮説が真の場合に帰無仮説を棄却する確率を表し、これはタイプIエラーや偽陽性として知られるエラーの一種です。

たとえば、テストを5％の有意水準（α = 0.05）で設定すると、帰無仮説が真の場合に帰無仮説を棄却するリスクが5％あります。この0.05のレベルはαの一般的な選択肢ですが、コンテキストや研究の分野に応じて0.01や0.10などの他のレベルも使用できます。

テストのサイズが小さいほど、帰無仮説を棄却するために必要な証拠が強くなり、タイプIエラーの可能性が低くなりますが、タイプIIエラー（帰無仮説が偽であるにもかかわらず帰無仮説を棄却しないエラー）の可能性が高まる可能性があります。タイプIエラーとタイプIIエラーのバランスは、任意の統計テストの設計において重要な考慮事項です。

実測サイズ

モンテカルロシミュレーションを通じた仮説検定の文脈での実測サイズは、帰無仮説が真の場合にシミュレーション全体で帰無仮説が誤って棄却される割合を指します。これは実質的にはタイプIエラー率のシミュレートされたバージョンです。

以下は、これを行う一般的なプロセスです：

1. 帰無仮説を設定し、テストの有意水準（たとえばα = 0.05）を選択します。

2. 帰無仮説が真であるという仮定の下で、大量のサンプルを生成します。結果の安定性を確保するために、サンプル数は通常非常に大きく、10,000個または100,000個などが使用されます。

3. 各サンプルについて、仮説検定を実行し、帰無仮説が棄却されたかどうかを記録します（棄却された場合は1、棄却されなかった場合は0として記録できます）。

4. 実測サイズを、帰無仮説が棄却されたシミュレーションの割合として計算します。これは与えられた検定手順の下で帰無仮説を棄却する確率を推定します。

以下のコードは、これの実装方法を示しています。

import numpy as npfrom scipy.stats import ttest_1sampimport randomrandom.seed(10)def calculate_empirical_size(num_simulations: int, sample_size: int, true_mean: float, significance_level: float) -> float:    """    サンプルセットをシミュレートし、それぞれの仮説検定を実行し、経験的なサイズを計算します。    パラメータ：    num_simulations（int）：実行するシミュレーションの数。    sample_size（int）：各シミュレートされたサンプルのサイズ。    true_mean（float）：帰無仮説の下での真の平均。    significance_level（float）：仮説検定の有意水準。    戻り値：    float：経験的なサイズ、または帰無仮説が棄却されたテストの割合。    """    import numpy as np    from scipy.stats import ttest_1samp    # 帰無仮説の棄却回数のカウンターを初期化    rejections = 0    # シミュレーションを実行する    np.random.seed(0)  # 再現性のために    for _ in range(num_simulations):        sample = np.random.normal(loc=true_mean, scale=1, size=sample_size)        t_stat, p_value = ttest_1samp(sample, popmean=true_mean)        if p_value < significance_level:            rejections += 1    # 経験的なサイズを計算する    empirical_size = rejections / num_simulations    return empirical_sizecalculate_empirical_size(1000, 1000, 0, 0.05)

1000回のシミュレーションごとに、平均0、標準偏差1の正規分布からサイズ1000のランダムサンプルが抽出されます。1標本t検定を実施して、サンプル平均が真の平均（この場合は0）と有意に異なるかどうかをテストします。テストのp値が有意水準（0.05）より小さい場合、帰無仮説は棄却されます。

経験的なサイズは、帰無仮説が棄却された回数（誤った陽性）をシミュレーションの総数で割ったものです。この値は、よくキャリブレーションされたテストでは名目上の有意水準に近いはずです。この場合、関数は経験的なサイズを返し、シミュレーションと同じ条件を前提とした

DGPにおける共変量のない実験

以下では、結果が処置とランダムエラーにのみ影響を受けるDGPに従うデータをシミュレートしています。

y_i = tau*T_i+e_i

結果が処置のみに影響を受ける場合、処置効果パラメータの推定値は、比較的小さいサンプルサイズでも正確であり、サンプルサイズが増加するにつれて真のパラメータ値に収束します。以下のコードでは、パラメータtauの値を2に設定しています。

tau = 2corr = .5p = 10p0 = 0 # DGPNに使用される共変量の数Nrange = range(10,1000,2) # Nの値の範囲(nvalues,tauhats,sehats,lb,ub) = fn_run_experiments(tau,Nrange,p,p0,corr)caption = """共変量のないランダム化実験における処置効果パラメータの推定結果"""fn_plot_with_ci(nvalues,tauhats,tau,lb,ub,caption)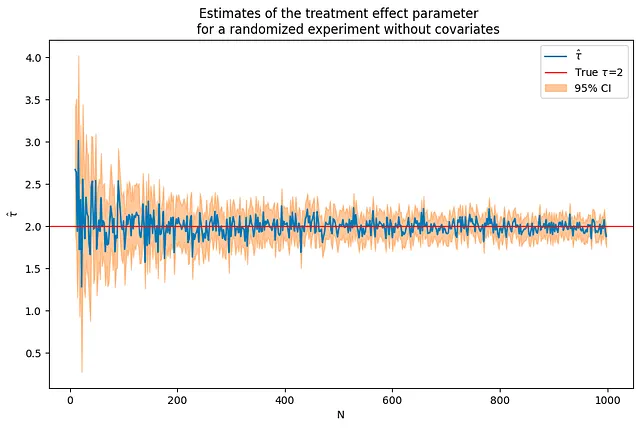

選択されたサンプルサイズで、これが切片を持つ回帰と同じであることを確認します。

切片と処置のOLS回帰を実行することで、同じ結果が得られることを確認できます。

N = 100Yexp,T = fn_generate_data(tau,N,10,0,corr)Yt = Yexp[np.where(T==1)[0],:]Yc = Yexp[np.where(T==0)[0],:]tauhat,se_tauhat = fn_tauhat_means(Yt,Yc)# n_values = n_values + [N]# tauhats = tauhats + [tauhat]lb = lb + [tauhat-1.96*se_tauhat]ub = ub + [tauhat+1.96*se_tauhat]print(f"平均の差を計算して得られるパラメータの推定値と標準誤差：{tauhat:.5f},{se_tauhat:.5f}")const = np.ones([N,1])model = sm.OLS(Yexp,np.concatenate([T,const],axis = 1))res = model.fit()print(f"切片を持つOLS回帰で得られるパラメータの推定値と標準誤差：{res.params[0]:.5f},{ res.HC1_se[0]:.5f}")

Rのモンテカルロ反復を実行し、バイアス、RMSE、およびサイズを計算します

今度は、Nパラメータの値のリストをループしてサンプルサイズを増やし、各反復でテストのRMSE、バイアス、および実際のサイズを計算します。

このPythonスクリプトは、共変量を考慮しない場合のA/Bテストの性能のバイアス、RMSE、およびサイズにサンプルサイズ(N)がどのように影響するかを研究するための実験シミュレーションを実施します。ステップごとに詳細を説明します。

1. estDict = {}は、実験結果を保存するための空の辞書を初期化します。

2. R=2000は、実験の繰り返し回数を2000に設定します。

3. for N in [10,50,100,500,1000]は、異なるサンプルサイズについてループします。

4. このループ内で、tauhats=[], sehats=[]は、各実験の推定処置効果tauhatとそれに対応する標準誤差se_tauhatを保存するための空のリストとして初期化されます。

5. for r in tqdm(range(R)):は、R回の実験をループします。進捗バーはtqdmによって提供されます。

6. Yexp,T = fn_generate_data(tau,N,10,0,corr)は、事前定義された処置効果tau、観測値の数N、10個の共変量、非ゼロ係数を持たない共変量、および事前定義された相関を持つ各実験の合成データを生成します。

7. Yt = Yexp[np.where(T==1)[0], :] および Yc = Yexp[np.where(T==0)[0], ;] は合成データを処理群と対照群に分割します。

8. tauhat, se_tauhat = fn_tauhat_means(Yt, Yc)は処置効果の推定値とその標準誤差を計算します。

9. tauhats = tauhats + [tauhat] および sehats = sehats + [se_tauhat] は処置効果の推定値とその標準誤差を対応するリストに追加します。

10. estDict[N] = {'tauhat': np.array(tauhats).reshape([len(tauahts), 1]), 'sehat': np.array(sehats).reshape([len(sehats), 1])} はサンプルサイズをキーとして推定値を辞書に格納します。

11. tau0 = tau * np.ones([R, 1]) は真の処置効果と同じ値を持つ R サイズの配列を作成します。

12. estDict の各サンプルサイズについて、スクリプトは fn_bias_rmse_size() 関数を使用してバイアス、RMSE、および処置効果の推定値のサイズを計算し、結果を表示します。

サンプルサイズが増えるにつれて、バイアスとRMSEが減少し、サイズが真のサイズである0.05に近づくことが予想されます。

estDict = {}
R = 2000
for N in [10, 50, 100, 500, 1000]:
    tauhats = []
    sehats = []
    for r in tqdm(range(R)):
        Yexp, T = fn_generate_data(tau, N, 10, 0, corr)
        Yt = Yexp[np.where(T==1)[0], :]
        Yc = Yexp[np.where(T==0)[0], :]
        tauhat, se_tauhat = fn_tauhat_means(Yt, Yc)
        tauhats = tauhats + [tauhat]
        sehats = sehats + [se_tauhat]
    estDict[N] = {
        'tauhat': np.array(tauhats).reshape([len(tauhats), 1]),
        'sehat': np.array(sehats).reshape([len(sehats), 1])
    }
    tau0 = tau * np.ones([R, 1])
for N, results in estDict.items():
    (bias, rmse, size) = fn_bias_rmse_size(tau0, results['tauhat'], results['sehat'])
    print(f'N={N}: bias={bias}, RMSE={rmse}, size={size}')

100%|██████████| 2000/2000 [00:00<00:00, 3182.81it/s]
100%|██████████| 2000/2000 [00:00<00:00, 2729.99it/s]
100%|██████████| 2000/2000 [00:00<00:00, 2238.62it/s]
100%|██████████| 2000/2000 [00:04<00:00, 479.67it/s]
100%|██████████| 2000/2000 [02:16<00:00, 14.67it/s]
N=10: bias=0.038139125088721144, RMSE=0.6593256331782233, size=0.084
N=50: bias=0.002694446014687934, RMSE=0.29664599979723183, size=0.0635
N=100: bias=-0.0006785229668018156, RMSE=0.20246779253127453, size=0.0615
N=500: bias=-0.0009696751953095926, RMSE=0.08985542730497854, size=0.062
N=1000: bias=-0.0011137216061364087, RMSE=0.06156258265280801, size=0.047

DGPでの共変量を用いた実験

次に、DGPに共変量を追加します。今回は治療効果だけでなく、いくつかの他の変数 X にも結果が依存するようになります。以下のコードは、DGPに含まれる50個の共変量を使用してデータをシミュレートします。前回の共変量を使用しないシミュレーションと同じサンプルサイズと処置効果パラメータを使用すると、今回の推定値はよりノイズが多くなりますが、それでも正しい解に収束することがわかります。

y_i = tau*T_i + beta*x_i + e_i

以下のプロットは、2つのDGPsからの推定値を比較しています。共変量がDGPsに導入された場合、推定値がどれだけノイズが多くなるかがわかります。

tau = 2corr = .5p = 100p0 = 50 # DGPsで使用される共変量の数Nrange = range(10,1000,2) # Nの値でループする(nvalues_x,tauhats_x,sehats_x,lb_x,ub_x) = fn_run_experiments(tau,Nrange,p,p0,corr)caption = """DGPにおけるXを使用したランダム化実験の治療効果パラメータの推定値ですが、推定器にはXが含まれていません"""fn_plot_with_ci(nvalues_x,tauhats_x,tau,lb_x,ub_x,caption)# 共変量を使用しないように実験を再実行p0 = 0 # DGPsで使用される共変量の数Nrange = range(10,1000,2) # Nの値でループする(nvalues_x0,tauhats_x0,sehats_x0,lb_x0,ub_x0) = fn_run_experiments(tau,Nrange,p,p0,corr)fig = plt.figure(figsize = (10,6))plt.title("""DGPにおけるXを使用したランダム化実験の治療効果パラメータの推定値ですが、大きなNではズームインしてください""")plt.plot(nvalues_x[400:],tauhats_x[400:],label = '$\hat{\\tau}^{(x)}$')plt.plot(nvalues_x[400:],tauhats_x0[400:],label = '$\hat{\\tau}$',color = 'green')plt.legend()fig = plt.figure(figsize = (10,6))plt.title("""共変量の有無でのDGPからの治療効果の推定値ですが、大きなNではズームインしてください""")plt.plot(nvalues_x[400:],tauhats_x[400:],label = '$\hat{\\tau}^{(x)}$')plt.plot(nvalues_x[400:],tauhats_x0[400:],label = '$\hat{\\tau}$',color = 'green')plt.legend()

100%|██████████| 495/495 [00:41<00:00, 12.06it/s]100%|██████████| 495/495 [00:42<00:00, 11.70it/s]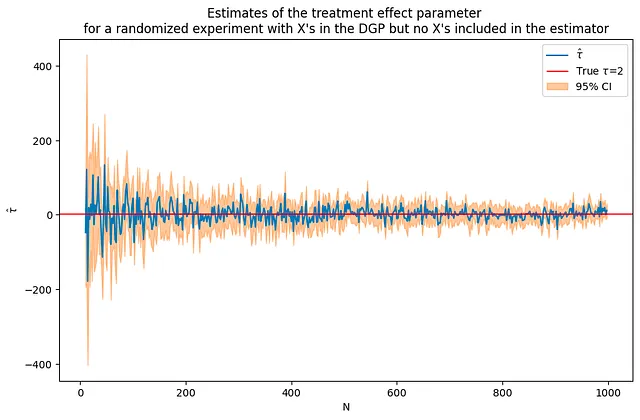

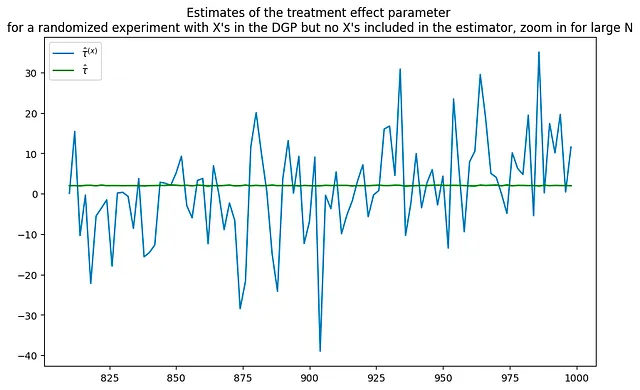
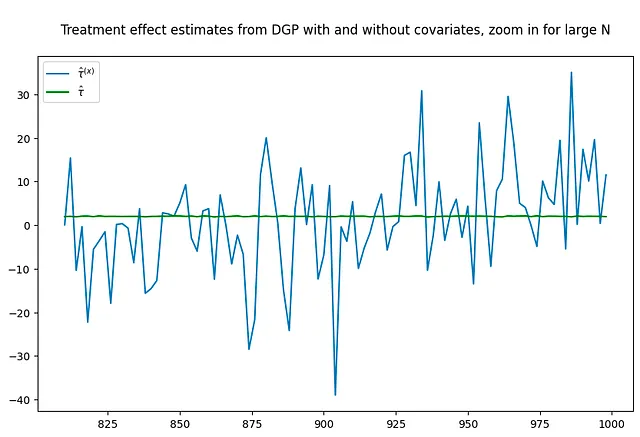
実験を非常に大きなサンプルサイズで繰り返しても、問題は解消されるでしょうか？必ずしもそうではありません。サンプルサイズの増加にもかかわらず、推定値はまだかなりノイズが多いように見えます。

tau = 2corr = .5p = 100p0 = 50 # DGPsで使用される共変量の数Nrange = range(1000,50000,10000) # Nの値でループする(nvalues_x2,tauhats_x2,sehats_x2,lb_x2,ub_x2) = fn_run_experiments(tau,Nrange,p,p0,corr)fn_plot_with_ci(nvalues_x2,tauhats_x2,tau,lb_x2,ub_x2,caption)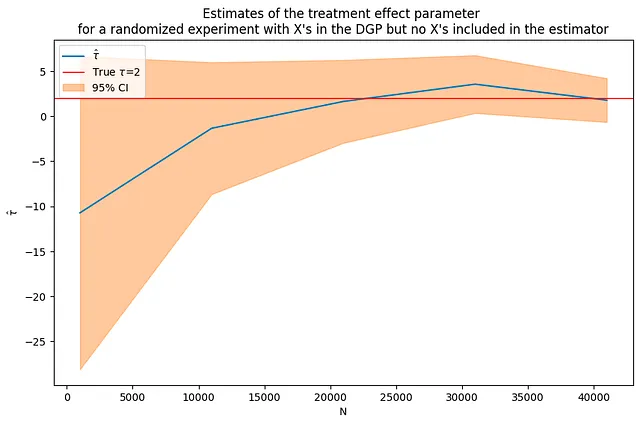

Xを含むDGP – 回帰に共変量を追加する

この部分では、前と同じDGPを使用します：

y_i = tau*T_i + beta*x_i + e_i

これから、回帰モデルにこれらの共変量Xを含めます。これにより、推定値の精度が大幅に向上することがわかります。ただし、これは少し「手抜き」です – この場合、正しい共変量を最初から含めています。

実世界のシナリオでは、含めるべき「適切な」共変量がわからない場合があり、さまざまなモデルと共変量を試す必要があるかもしれません。

tau = 2corr = .5p = 100p0 = 50 # DGPNで使用される共変量の数range = range(100,1000,2) # N値のループ# pよりも多くの観測値から始める必要があるflagX = 1(nvalues2,tauhats2,sehats2,lb2,ub2) = fn_run_experiments(tau,Nrange,p,p0,corr,flagX)caption = """右のXを使用した回帰で得られた推定値を使用したランダム化実験の治療効果パラメータの推定"""fn_plot_with_ci(nvalues2,tauhats2,tau,lb2,ub2,caption)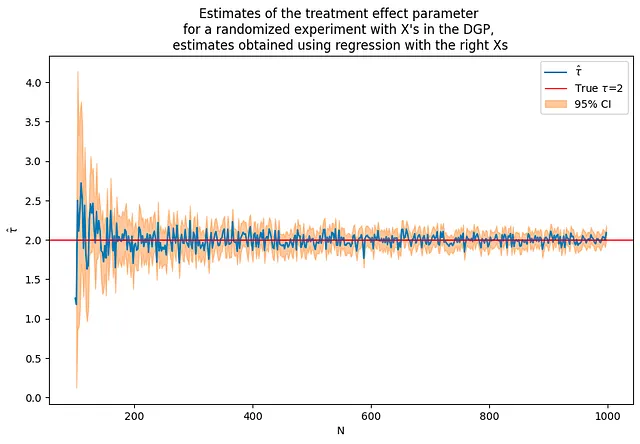

アウトカムに影響を与えるXと影響を与えないXを組み合わせた場合、どうなるのでしょうか？

このセクションでは、回帰モデルに関連する共変量と関連しない共変量を含めることを検討します。これは、共変量がアウトカムに影響を与えるかどうかが明確でない実世界のシナリオを模倣しています。

非関連の変数を含める場合でも、共変量を含めなかった場合と比較して、全体的な推定値は改善する傾向があります。ただし、関連する共変量のみを含めた場合と比較して、関連しない変数を含めると推定値にノイズと不確実性が導入され、精度が低下する可能性があります。

結論として、データの共変量の影響を理解することは、A/Bテストの結果の精度と信頼性を向上させるために不可欠です。このチュートリアルでは、RMSE、バイアス、サイズなどの推定器の統計的特性をモンテカルロシミュレーションを通じて推定し理解する方法を探求しています。また、DGPと回帰モデルに共変量を含めることの影響を強調し、実践における慎重なモデル選択と仮説検定の重要性を示しています。

# 前と同じDGPを使用tau = 2corr = .5p = 100p0 = 50 # DGPNで使用される共変量の数a = 0.9b = 0.1Nrange = range(100,1000,2) # N値のループ# pよりも多くの観測値から始める必要があるflagX = 2(nvalues3,tauhats3,sehats3,lb3,ub3) = fn_run_experiments(tau,Nrange,p,p0,corr,flagX,a,b)caption = f"""{100*a:.1f}%の正しいXと{100*b:.1f}%の関連しないXを使用した回帰で得られた推定値を使用したランダム化実験の治療効果パラメータの推定"""fn_plot_with_ci(nvalues3,tauhats3,tau,lb3,ub3,caption)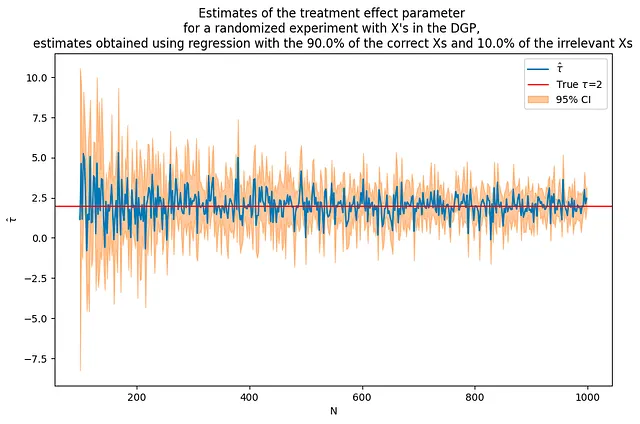

特に明記されていない場合、すべての画像は著者のものです。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!