A/Bテストの意味を理解する：厳しい質問でよりよく理解する

A/Bテストの意味を理解するためには、厳しい質問でよりよく理解しましょう

A/Bテストの直感に反する側面を挑戦的な問題を通じて明らかにし、理解を深めてミスを避けましょう

この記事では、実験の文脈での一般的な統計的エラーに焦点を当てています。これは、多くの人が直感的でないと感じる答え付きの5つの質問として設定されています。これは、すでにA/Bテストに精通しているが、理解を広げたい人を対象としています。これにより、日常の業務で一般的なエラーや面接での成功につながるかもしれません。

質問1：A/Bテスト（α = 0.05、β = 0.2）を実施し、統計的に有意な結果が得られた場合、それが真の陽性である可能性は何％ですか？

仮説がすべて機能する場合、成功したA/Bテストの100％が真の陽性です。仮説が機能しない場合、成功したA/Bテストの100％が偽の陽性です。

これらの2つの極端な例は、仮説の分布についての仮定なしでは、この質問に答えることができないことを示しています。

• JavaScriptを使用してOracleデータベース内からHugging Face AIを呼び出す方法
• LangChainを使用したLLMパワードアプリケーションの構築
• LangChain：LLMがあなたのコードとやり取りできるようにします

もう一度試してみましょう。テストする仮説の10％が有効であると仮定しましょう。その場合、A/Bテストから統計的に有意な結果が得られた場合、それが真の陽性である確率は64％（ベイズの定理による、(1–0.2)*0.1 / ((1–0.2)*0.1 + 0.05*(1–0.1))）です。

質問2：帰無仮説が真である場合、より高いp値またはより低いp値の方がより可能性が高いですか？

多くの人は前者だと思います。これは直感的です：効果がない場合、結果は統計的に有意でない可能性が高いため、より高いp値です。

しかし、答えはいずれでもありません。帰無仮説が真である場合、p値は一様に分布しています。

混乱が生じるのは、人々がこれらの概念を通常分布のzスコア、またはサンプル平均、またはサンプル平均の差として視覚化することが多いためです。これらはすべて正規分布しています。そのため、p値の一様性を理解するのは困難かもしれません。

シミュレーションでこれを説明しましょう。治療群と対照群の両方が同じ正規分布（μ = 0、σ = 1）から抽出されると仮定します（つまり、帰無仮説が真である）。それぞれの平均値を比較し、p値を計算し、このプロセスを複数回繰り返します。単純化のため、治療群の平均値が大きいケースのみを見ることにします。そして、p値が0.9から0.8および0.2から0.1の範囲の場合を見てみましょう。

シミュレーションした分布上にこれらのp値の範囲をマッピングすると、より明確になります。ピークはゼロ付近で高くなりますが、ここでは幅が狭くなります。逆に、ゼロから離れるにつれて、ピークは縮小しますが、区間の幅は広がります。これは、p値が等しい長さの区間が曲線の下の同じ面積を包含するように計算されるためです。

質問3：いくつかの技術的またはビジネス上の制約により、通常よりも小さなサンプルサイズでA/Bテストを実行しました。結果はわずかに有意です。ただし、効果サイズは大きく、類似のA/Bテストで通常見られるよりも大きいです。より大きな効果サイズは結果への信頼性を高めるべきでしょうか？

実際には、そうではありません。効果が有意であるためには、ゼロからプラスまたはマイナス2倍の標準誤差離れる必要があります（α = 0.05の場合）。サンプルサイズが小さくなると、標準誤差は一般的に上昇します。これは、サンプルサイズが小さい場合に統計的に有意な効果が大きくなる傾向があることを意味します。

以下のシミュレーションは、次のことを示しています：両グループ（N=1000）が同じ正規分布（μ=0、σ=1）からサンプリングされた場合の、有意なA/Bテストの絶対効果サイズです。

質問4：前の質問から得た理解を基に考えましょう 。2つの標準誤差よりも小さい真の効果を検出することは可能ですか？

はい、ただし、ここでは意味合いが曖昧です。真の効果サイズは2つの標準誤差よりも著しく小さいかもしれません。それでも、一定の割合のA/Bテストが統計的有意性を示すことが予想されます。

ただし、これらの条件下では、検出される効果サイズは常に誇張されます。真の効果が0.4であると想像してくださいが、p値が0.05で0.5の効果が検出されたとします。これを真の陽性と考えますか？真の効果サイズがわずか0.1である場合にも、0.5の効果が検出された場合はどうでしょうか？真の効果がわずか0.01である場合、それはまだ真の陽性と言えるでしょうか？

このシナリオを視覚化してみましょう。制御グループ（N=100）は正規分布（μ=0、σ=2）からサンプリングされますが、処理グループ（N=100）は同じ分布からサンプリングされ、ただしμは0.1から1まで変動します。真の効果サイズに関係なく、成功したA/Bテストは少なくとも0.5の推定効果サイズを生成します。真の効果がこれよりも小さい場合、推定結果は明らかに誇張されます。

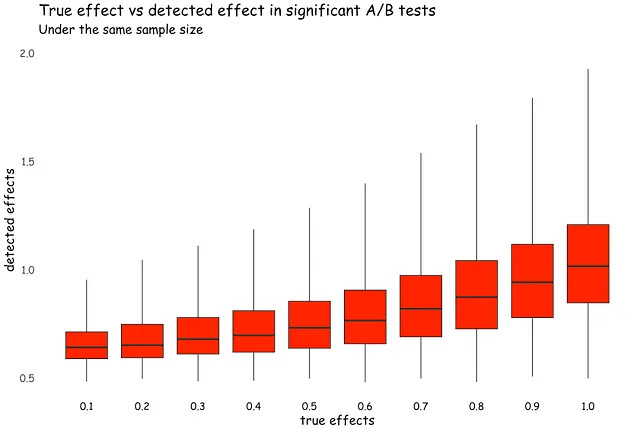
これが、一部の統計学者が「真の陽性」と「偽の陽性」のような2つのバイナリカテゴリに結果を分類するのを避ける理由です。代わりに、より連続的な方法で扱います[1]。

質問5：p値が0.04で有意な結果を示すA/Bテストを実施しましたが、上司はまだ納得せず、2回目のテストを要求します。この後続のテストでは有意な結果が得られず、p値は0.25です。これは元の効果が実際には存在せず、最初の結果が偽の陽性だったことを意味しますか？

p値をバイナリ、辞書的な意思決定規則として解釈することには常にリスクがあります。実際のp値が何を意味するかを思い出しましょう。それは驚きの尺度です。そして、それはランダムで連続的です。そして、それはただ1つの証拠です。

最初の実験（p=0.04）は1,000人のユーザーで実施されました。2番目の実験（p=0.25）は10,000人のユーザーで実施されました。品質の顕著な違いに加えて、3番目と4番目の質問で議論したように、2番目のA/Bテストはおそらくもはや実用的に有意ではないほど小さな推定効果サイズを持っていたかもしれません。

このシナリオを逆に考えてみましょう：最初の実験（p=0.04）は10,000人で実施され、2番目の実験（p=0.25）は1,000人で実施されました。ここでは、効果が「存在する」という確信度が高くなります。

さて、2つのA/Bテストが同一であると想像してみてください。この状況では、2つのかなり似た、やや驚きのある結果が観察されますが、どちらもヌル仮説とはあまり一致していません。.05の反対側に落ちるという事実はあまり重要ではありません。重要なのは、ヌル仮説が真である場合に2つの小さなp値が連続して観察されることはまれであるということです。

考慮すべきもう1つの質問は、この違い自体が統計的に有意であるかどうかです。p値をバイナリ的な方法で分類することは、直感を歪め、閾値の異なる側にあるp値間に広大でありさえ存在論的な違いがあるかのように思わせるかもしれません。しかし、p値はかなり連続的な関数であり、異なるp値を持つ2つのA/Bテストが、ヌル仮説に対する非常に似た証拠を示している可能性があるということがあります[2]。

これを別の視点から見るもう1つの方法は、証拠を組み合わせることです。両方のテストに対してヌル仮説が真であると仮定すると、フィッシャーの方法によると、結合されたp値は0.05になります。p値を組み合わせるための他の方法もありますが、一般的な論理は同じです。ほとんどの状況では、鮮明なヌルは現実的な仮説ではありません。したがって、個々に統計的に有意ではないかもしれない「驚き」の結果が十分にあれば、ヌルを棄却するのに十分です。

結論

A/Bテストを分析するために一般的に使用する帰無仮説検定フレームワークは、特に直感的ではありません。定期的な精神的な練習がないと、しばしば「直感的な」理解に戻ってしまい、誤解を招くことがあります。また、この認知負荷を軽減するためのルーティンを開発することもあります。残念ながら、これらのルーティンはしばしば何らかの儀式的な要素を持ち、形式的な手順の遵守が推論の実際の目的を覆い隠すことがあります。

参考文献

1. McShane, B. B., Gal, D., Gelman, A., Robert, C., & Tackett, J. L. (2019). Abandon statistical significance. The American Statistician , 73 (sup1), 235–245.
2. Gelman, A., & Stern, H. (2006). The difference between “significant” and “not significant” is not itself statistically significant. The American Statistician , 60 (4), 328–331.

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!