類似検索、パート6：LSHフォレストによるランダム射影

類似検索、パート6：LSHフォレスト

ランダムハイパープレーンを構築してデータのハッシュ化と類似性の反映を理解する

「類似性検索」とは、クエリが与えられた場合、データベース内のすべてのドキュメントの中からそれに最も類似したドキュメントを見つけることを目的とした問題です。

導入

データサイエンスでは、類似性検索はNLP領域、検索エンジン、またはレコメンドシステムなどで頻繁に使用され、クエリに対して最も関連性の高いドキュメントやアイテムを取得する必要があります。大量のデータの検索性能を向上させるためのさまざまな方法が存在します。

前回は、LSHの主なパラダイムである入力ベクトルを低次元のハッシュ値に変換し、類似性に関する情報を保持する方法を見てきました。ハッシュ値（シグネチャ）を取得するためには、minhash関数が使用されました。この記事では、入力データをランダムに射影して類似したバイナリベクトルを得る方法について説明します。

• このAI論文では、「Retentive Networks（RetNet）」を大規模言語モデルの基礎アーキテクチャとして提案していますトレーニングの並列化、低コストの推論、そして良好なパフォーマンスを実現しています
• マルチディフュージョンによる画像生成のための統一されたAIフレームワーク、事前学習されたテキストから画像へのディフュージョンモデルを使用して、多目的かつ制御可能な画像生成を実現します
• 「機械学習モデルのバリデーション方法」

類似性検索、パート5：局所敏感ハッシング（LSH）

類似性情報をハッシュ関数に組み込む方法を探る

towardsdatascience.com

アイデア

高次元空間に存在する一群の点を考えてみましょう。ランダムなハイパープレーンを構築することで、それぞれの点を正と負の2つのサブグループに分けることができます。正の側には「1」が割り当てられ、負の側には「0」が割り当てられます。

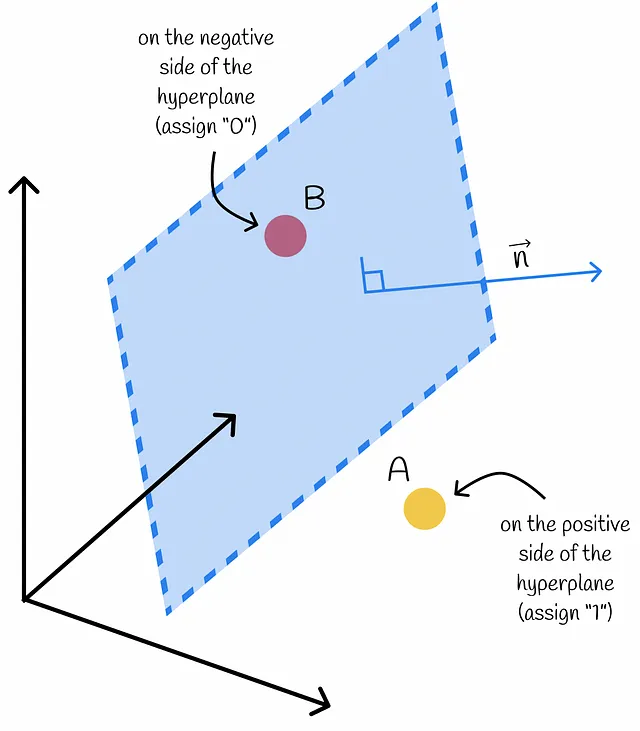
あるベクトルのハイパープレーンの側はどのように決定されるのでしょうか？内積を使用することで判定できます！線型代数の本質に迫ると、与えられたベクトルとハイパープレーンの法線ベクトルの内積の符号によって、ベクトルがどの側にあるかが決まります。これにより、データセットの各ベクトルは2つの側のいずれかに分離されます。

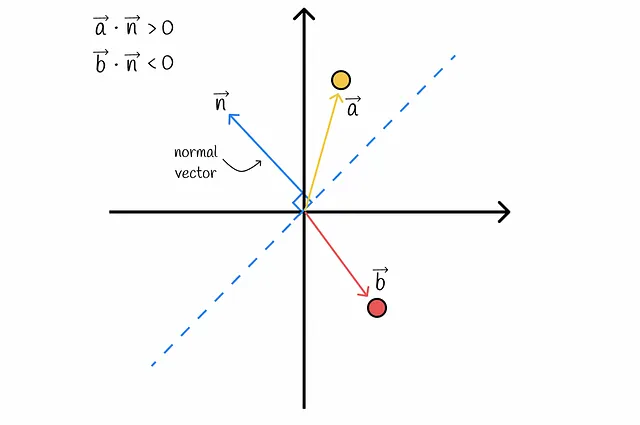
明らかに、データセットの各ベクトルを1つのバイナリ値でエンコードするだけでは不十分です。したがって、複数のランダムハイパープレーンを構築する必要があります。これにより、各ベクトルは特定のハイパープレーンに対する相対的な位置に基づいて、0と1の複数の値でエンコードされます。2つのベクトルが完全に同じバイナリコードを持つ場合、構築されたハイパープレーンのどれもそれらを異なる領域に分離することができなかったことを示しています。したがって、実際には非常に近い可能性があります。

与えられたクエリの最近傍点を見つけるためには、クエリをすべてのハイパープレーンに対して相対的な位置を調べ、0と1でエンコードするだけで十分です。クエリのために見つかったバイナリベクトルは、データセットベクトル用に得られたすべての他のバイナリベクトルと比較することができます。これは、ハミング距離を使用して線形に行うことができます。

2つのベクトル間のハミング距離は、その値が異なる位置の数です。

クエリに対してハミング距離が最も少ないバイナリベクトルが候補として選ばれ、初期クエリと完全に比較されます。

なぜハイパープレーンはランダムに構築されるのですか？

現時点では、ハイパープレーンがランダムに構築される理由と、データセットのポイントを分離するためのカスタムルールが定義されていない決定論的な意味での方法を要求するのは論理的に思えます。これには2つの主な理由があります：

• まず第一に、決定論的なアプローチはアルゴリズムを一般化することができず、オーバーフィッティングを引き起こす可能性があります。
• 第二に、ランダム性により、アルゴリズムのパフォーマンスに関する確率的な声明をすることが可能になります。これは入力データに依存しないからです。決定論的なアプローチでは、これはうまく機能するかもしれませんが、別のデータではパフォーマンスが低下する可能性があります。これについての良い類似例は、決定論的なクイックソートアルゴリズムです。これは平均して O(n * log n) の時間で動作しますが、最悪の場合ではソート済みの配列では O(n²) の時間がかかります。アルゴリズムのワークフローに関する知識がある場合、常に最悪のケースのデータを提供することでシステムの効率を大幅に損なうことができます。そのため、ランダム化されたクイックソートのほうがはるかに好まれます。ランダムハイパープレーンでもまったく同様の状況が発生します。

LSHランダムプロジェクションはなぜ「ツリー」とも呼ばれるのですか？

ランダムプロジェクション法は、時々LSHツリーと呼ばれます。これは、ハッシュコードの割り当てプロセスを現在のハイパープレーンの負の側または正の側にベクトルがあるかどうかの条件を含む意思決定ツリーの形式で表現できるためです。

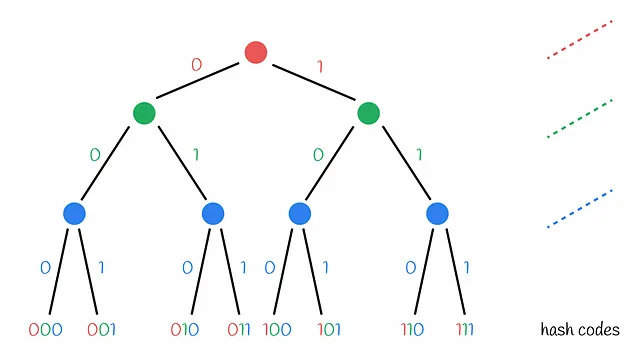
ハイパープレーンの集合

ハイパープレーンはランダムに構築されます。これにより、データセットのポイントをうまく分離できないシナリオが発生する場合があります。以下の図に示されています。

技術的には、2つのポイントが同じハッシュコードを持ちながら互いに遠くにある場合は大したことではありません。アルゴリズムの次のステップでは、これらのポイントが候補として取り込まれ、完全に比較されます。これにより、誤検出されたケースを除外することができます。誤検出の場合はより複雑です。2つのポイントが異なるハッシュコードを持つが実際には近くにある場合です。

なぜ古典的な機械学習の決定木と同様のアプローチを使用しないのですか？それらはランダムフォレストに組み合わされて、全体的な予測品質を向上させることができます。1つの推定器がエラーを犯した場合、他の推定器がより良い予測を行い、最終的な予測エラーを緩和することができます。このアイデアを利用すると、ランダムハイパープレーンの構築プロセスを独立して繰り返すことができます。結果のハッシュ値は、前の章での最小ハッシュ値の場合と同様に、2つのベクトルのために集約されます：

もしクエリが別のベクトルと少なくとも一度同じハッシュコードを持っている場合、それらは候補とみなされます。

この仕組みを使用すると、誤りの陰性（false negative）の数を減らすことができます。

品質と速度のトレードオフ

データセット上で実行する適切な数のハイパープレーンを選ぶことが重要です。データセットのポイントを分割するために選択されるハイパープレーンが多いほど、衝突が少なくなり、ハッシュコードの計算にかかる時間と保存に必要なメモリが増えます。具体的には、データセットがn個のベクトルで構成され、k個のハイパープレーンで分割する場合、平均的にはすべての可能なハッシュコードがn / 2ᵏ個のベクトルに割り当てられます。

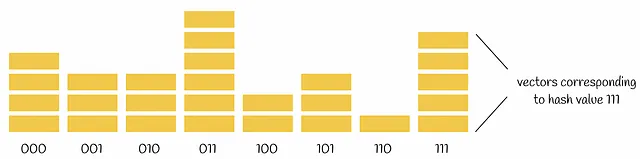
計算量

トレーニング

LSH Forestのトレーニングフェーズは2つのパートで構成されます：

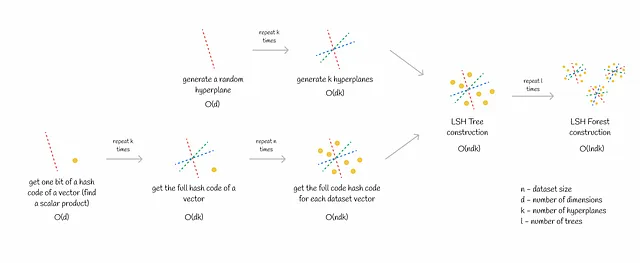
1. k個のハイパープレーンの生成。これは比較的高速な手順であり、d次元空間の単一のハイパープレーンを生成するのにO(d)の時間がかかります。
2. すべてのデータセットベクトルにハッシュコードを割り当てる。特に大規模なデータセットの場合、このステップには時間がかかる場合があります。単一のハッシュコードを取得するにはO(dk)の時間がかかります。データセットがn個のベクトルから構成される場合、合計の計算量はO(ndk)になります。

上記のプロセスは、フォレスト内の各ツリーに対して数回繰り返されます。

推論

LSH Forestの利点の一つは、高速な推論です。推論は次の2つのステップで行われます：

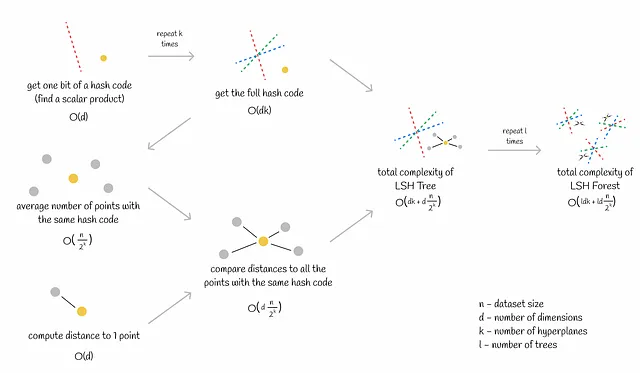
1. クエリのハッシュコードを取得する。これはk個のスカラー積を計算することに相当し、O(dk)の時間がかかります（dは次元数）。
2. 同じバケット（同じハッシュコードを持つベクトル）内のクエリに対する最近傍のベクトルを見つけるため、候補までの正確な距離を計算します。距離の計算はO(d)で線形に行われます。平均的に、各バケットにはn / 2ᵏ個のベクトルが含まれます。したがって、すべての候補への距離計算にはO(dn / 2ᵏ)の時間がかかります。

合計の計算量はO(dk + dn / 2ᵏ)です。

通常のように、上記のプロセスはフォレスト内の各ツリーに対して数回繰り返されます。

ハイパープレーンの数kがn ~ 2ᵏとなるように選ばれる場合（ほとんどの場合可能です）、合計の推論の計算量はO(ldk)となります（lはツリーの数）。基本的には、計算時間はデータセットのサイズに依存しないことを意味します！この微妙さにより、数百万または数十億のベクトルに対する類似性検索の効率的なスケーラビリティが実現されます。

エラーレート

LSHに関する前半の記事では、2つのベクトルが候補として選ばれる確率を、シグネチャの類似性に基づいて求める方法について説明しました。ここでは、ほぼ同じロジックを使用してLSH Forestの式を求めます。

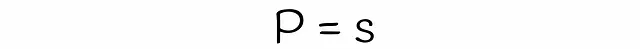
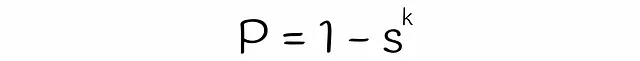
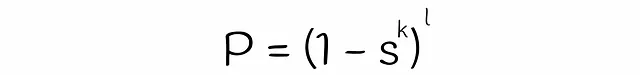
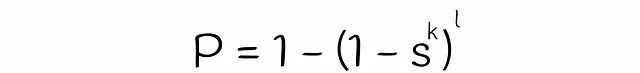
これまでに、2つのベクトルが候補である確率を推定するための式をほぼ得ることができました。唯一残っているのは、式中の変数sの値を推定することです。クラシックなLSHアルゴリズムでは、sは2つのベクトルのジャカード指数またはシグネチャ類似度と等しいです。一方、LSHフォレストでは、線形代数理論を使用してsを推定します。

正直に言うと、sは2つのベクトルaとbが同じビットを持つ確率です。この確率は、ランダムなハイパープレーンがこれらのベクトルを同じ側に分離する確率と同等です。これを可視化してみましょう：

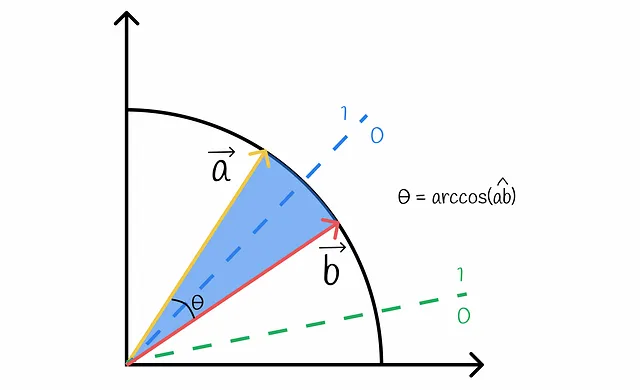
図から明らかなように、ハイパープレーンがベクトルaとbを分離し、異なる側に配置するのは、それらの間を通過する場合のみです。このような確率qは、簡単に計算できるベクトル間の角度に比例します：

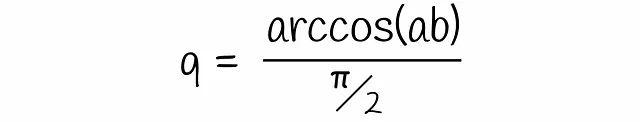
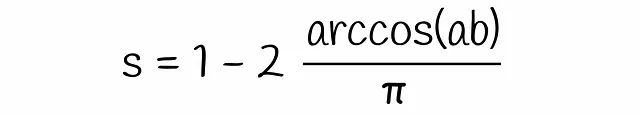
この式を先程得られた式に代入すると、最終的な式になります：

可視化

最後に得られた式を使用して、異なるハイパープレーンの数kおよびツリーの数lに基づいて、2つのベクトルが候補である確率をコサイン類似度に基づいて可視化してみましょう。

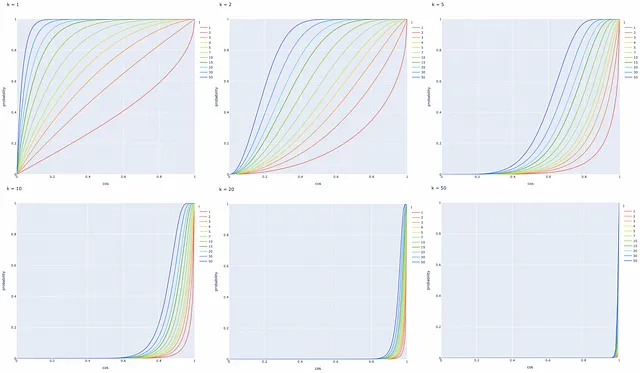
プロットに基づいていくつかの有用な観察ができます：

• コサイン類似度が1のベクトルのペアは常に候補になります。
• コサイン類似度が0のベクトルのペアは決して候補になりません。
• ハイパープレーンの数kが減少するか、LSHツリーの数lが増加すると、2つのベクトルが候補になる確率Pが増加します（つまり、偽陽性が増加します）。逆の主張も真です。

まとめると、LSHは非常に柔軟なアルゴリズムです：与えられた問題に基づいて異なる値kとlを調整し、問題の要件を満たす確率曲線を取得することが可能です。

例

次の例を見てみましょう。l = 5つのツリーがk = 10のハイパープレーンで構築されています。それ以外にも、コサイン類似度が0.8の2つのベクトルがあります。ほとんどのシステムでは、このようなコサイン類似度は、ベクトルが実際に非常に近いことを示しています。前のセクションの結果に基づくと、この確率はわずか2.5％です！明らかに、このような高いコサイン類似度に対しては非常に低い結果です。l = 5およびk = 10のこれらのパラメータを使用すると、非常に多くの偽陰性が発生します！以下の緑色の線は、この場合の確率を表しています。

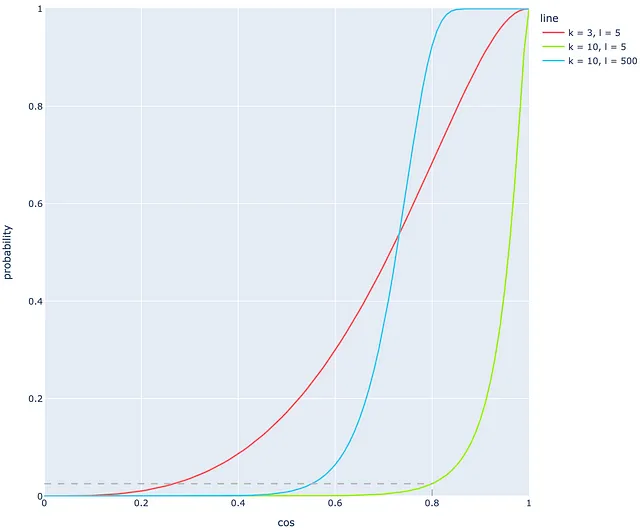
この問題は、より適切なkとlの値を調整することで解決できます。

例えば、kを3に減らすと（赤い線）、コサイン0.8の同じ値は以前よりも優れた68％の確率に対応します。初めに見ると、赤い線の方が緑の線よりも適しているように思えますが、赤い線のように小さなkの値を使用することは、非常に多くの衝突を引き起こします。そのため、2番目のパラメータであるツリーの数lを調整することを好む場合もあります。

kとは異なり、同様の線形状を得るには非常に高い数のツリーlが必要です。図では、青い線は緑の線からlの値を10から500に変更することで得られます。青い線は明らかに緑の線よりも適していますが、まだ完璧とは言えません：コサイン類似度が0.3-0.5の範囲で確率がほぼ0になるため、0.3-0.5のドキュメント類似度に対するこの小さな確率は好ましくありません。このような場合、実際の生活では0.3-0.5のドキュメント類似度の確率は通常よりも高くなるべきです。

最後の例に基づいて、非常に多くのツリー（多くの計算を必要とする）を使用しても、まだ多くの偽陰性が発生することが明らかです！これがランダムプロジェクション法の主な欠点です：

完璧な確率曲線を得ることは理論的に可能ですが、多くの計算が必要になるか、多くの衝突が発生します。そうでない場合、高い偽陰性率になります。

Faissの実装

Faiss（Facebook AI Search Similarity）は、最適化された類似検索に使用されるC++で書かれたPythonライブラリです。このライブラリは、データを効率的に格納し、クエリを実行するために使用されるデータ構造であるインデックスの異なるタイプを提供します。

Faissのドキュメントからの情報に基づいて、LSHインデックスの構築方法を調べます。

ランダムプロジェクションのアルゴリズムは、FaissのIndexLSHクラスの中で実装されています。Faissの作者は「ランダム回転」と呼ばれるわずかに異なる技術を使用していますが、これはこの記事で説明されているものと類似しています。このクラスは単一のLSHツリーのみを実装しています。LSHフォレストを使用したい場合は、単に複数のLSHツリーを作成し、その結果を集計するだけで十分です。

IndexLSHクラスのコンストラクタには2つの引数があります：

• d: 次元数
• nbits: 1つのベクトルをエンコードするのに必要なビット数（可能なバケットの数は2ⁿᵇᶦᵗˢと等しい）

search() メソッドで返される距離は、クエリベクトルまでのハミング距離です。

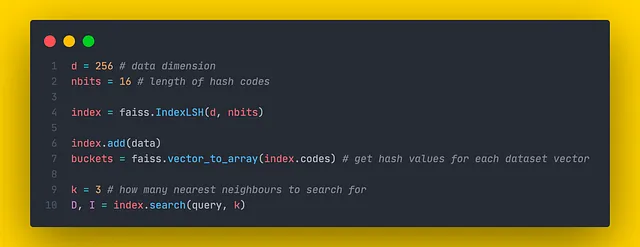
さらに、Faissでは、faiss.vector_to_array(index.codes) メソッドを呼び出すことで、各データセットベクトルのエンコードされたハッシュ値を調査することができます。

すべてのデータセットベクトルはnbitsのバイナリ値によってエンコードされるため、1つのベクトルを格納するのに必要なバイト数は次の式で計算できます：

Johnson-Lindenstraussの補題

Johnson-Lindenstraussの補題は、次元削減に関連する素晴らしい補題です。元の文言を完全に理解することは難しいかもしれませんが、簡単な言葉で表現すると次のようになります：

ランダムなサブセットを選び、元のデータをそれに射影することで、各点間の相対的な距離をほぼ保存することができます。

より正確に言うと、n個の点からなるデータセットがある場合、それらをO(logn)次元の新しい空間で表現することができます。このとき、点間の相対的な距離はほぼ保存されます。ベクトルがLSH法で約lognビットでエンコードされている場合、この補題を適用することができます。さらに、LSHは補題が要求するようにランダムな方法でハイパープレーンを作成します。

Johnson-Lindenstraussの補題の素晴らしい点の1つは、新しいデータセットの次元数が元のデータセットの次元数に依存しないという事実です！実際には、この補題は非常に小さい次元にはうまく機能しません。

結論

類似性検索のための強力なアルゴリズムを紹介しました。ランダムなハイパープレーンによる点の分離というシンプルなアイデアに基づいているため、大規模なデータセットでのパフォーマンスもスケーリングも非常に優れています。さらに、適切なハイパープレーンの数や木の選択を可能にする柔軟性も備えています。

Johnson-Lindenstraussの補題から得られる理論的な結果は、ランダム射影アプローチの使用を補強しています。

参考文献

• LSH Forest: 類似性検索のための自己チューニングインデックス
• Johnson-Lindenstraussの補題
• Faissドキュメント
• Faissリポジトリ
• Faissインデックスの概要

特記以外のすべての画像は著者のものです。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!