非ユークリッド空間における機械学習

非ユークリッド空間における機械学習' (Machine Learning in Non-Euclidean Space)

第II章: ハイパーボリックジオメトリーの直感を得る方法と、データサイエンスプロジェクトでの使用時期

この記事で学ぶこと

1. ユークリッド幾何学以外の異なる非ユークリッド幾何学の例として、球面幾何学とハイパーボリック幾何学があります。

2. ハイパーボリック空間は負の一定曲率を持つ空間です。

3. ハイパーボリック幾何学には異なるモデルがあり、最も有名なのはポアンカレ球モデルです。

• 「アルマンド・ソラール・レザマが初代ディスティングイッシュド・カレッジ・オブ・コンピューティング・プロフェッサーに任命されました」
• 「コーヒーマシンを介して侵害された – 知っておくべき6つのスマートホームセキュリティの脅威」
• 「Transformerモデルの実践的な導入 BERT」

4. 階層構造を持つデータセットの場合、ハイパーボリック空間で表現する方が良いです。なぜなら、ハイパーボリック空間と階層的データセットは、指数関数的な成長を持つからです。

私たちの会話

M: アニス、ハイパーボリックジオメトリーの背後にある直感を教えていただき、どのようなデータに関連性があるのか理解できるようにしていただけますか？ ハイパーボリックジオメトリーは、ユークリッド幾何学以外の一種の非ユークリッド幾何学であり、それは負の曲率を持ちます。

A: 最初に、非ユークリッド幾何学とは何でしょう？ユークリッドの第5公準（平行公準とも呼ばれる）というものがあります。これは次のプレイフェアの公理と同等です。「平面上で、与えられた直線と直線上にない点がある場合、その点を通る直線は最大で1本しか引けません。」これは当たり前のように思えますが、実際には常に真ではありません。実際、これはユークリッド空間でのみ真です。この公理が成立しない場合、非ユークリッド幾何学を考慮していることを意味します。この公理はまた、三角形公準とも等しいです。これは「すべての三角形の角の和は180°に等しい」と言います。

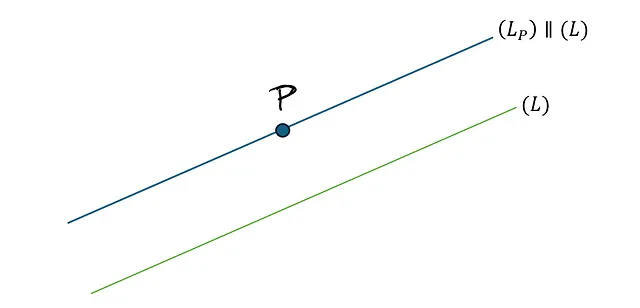
M: なるほど！それは平面性と曲率の概念に関連していますか？球面上では、三角形の角の和が180°より大きいことを知っています。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!