グラフが与えられたときの関数の微分可能性
関数の微分可能性

関数を考えます:
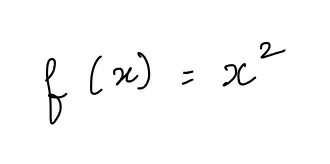
そのグラフは次のようになります:
- 「学生として、私がChatGPTを使って生産性を10倍にする方法」
- 「AIは本当に面接に合格するのを助けてくれるのでしょうか?」
- Streamlitの新しいConnections機能とインタラクティブなPlotlyマップでアプリを強化する
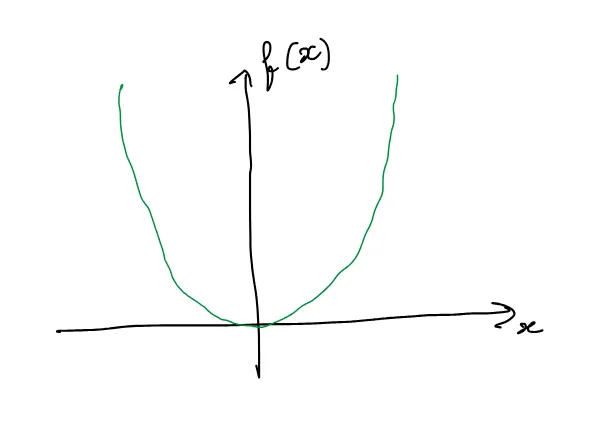
ある点での関数の導関数は、その点における接線の傾きです。この関数の場合、導関数は定義域内のすべての点xで存在します。しかし、これはすべての関数に当てはまるわけではありません。導関数が定義域内のすべての点で存在しない関数もあります。この記事では、導関数を持たない3つのタイプの点について見ていきます。
関数は、定義域内のすべての点xで導関数が存在する場合に形式的に微分可能と定義されます。つまり、定義域内の各点で一意な値を計算できる場合、それは微分可能と呼ばれます。
関数は、鉛筆を紙から離さずにグラフを描くことができる場合に連続とされます。
関数f(x) = |x|を考えましょう。次のように定義されます:
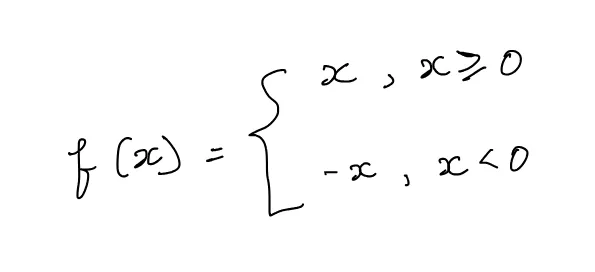
そのグラフは次のように描かれます:
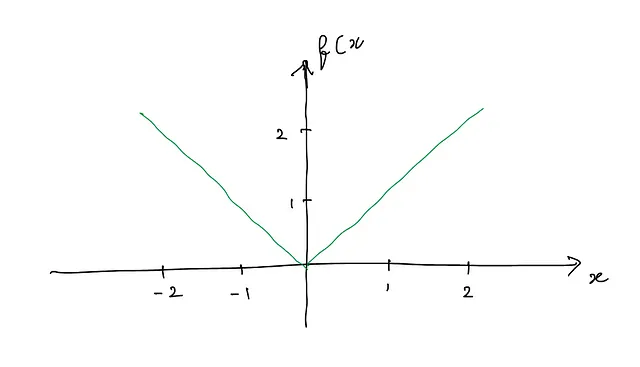
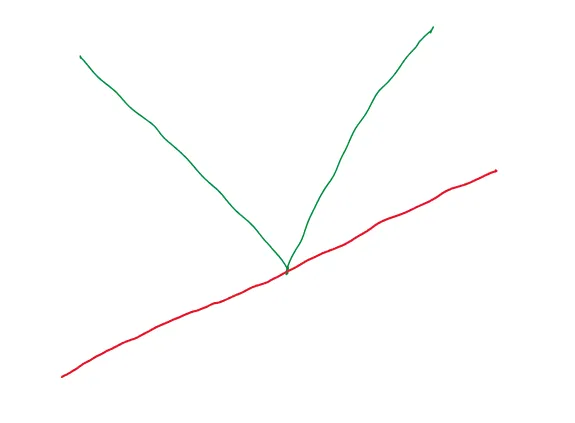
これは連続関数です。x=0で接線を引いてみましょう。次のように引くことができます(赤い線が接線です):
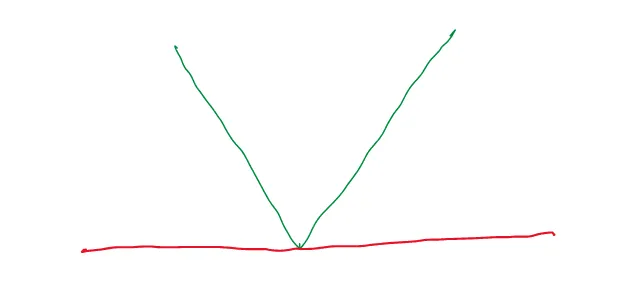
しかし、x=0で別の接線も引くことができます:
この直線も関数に一点で接します、つまりx=0です。したがって、これは確かに接線です。実際、この関数では、x=0で複数の接線が可能です:
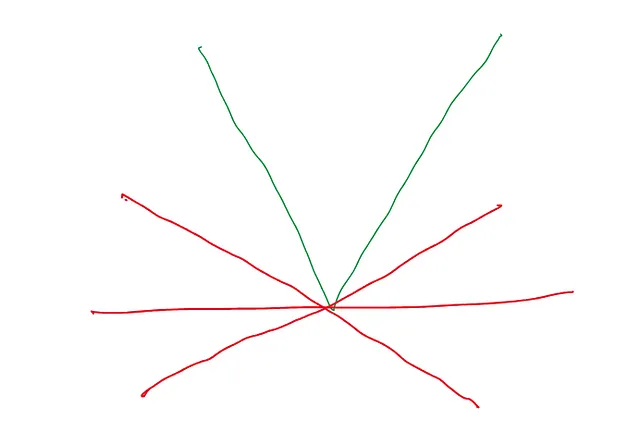
これは、x=0で接線の傾きに一意な値がないことを意味します。
それでは、極限の計算を見てみましょう。
f(x)の導関数は、次の極限の値として定義されます:
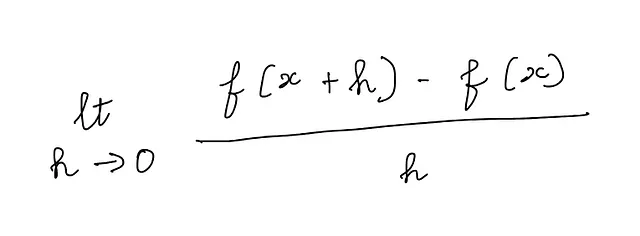
片側の極限を計算してみましょう:
左側の極限:
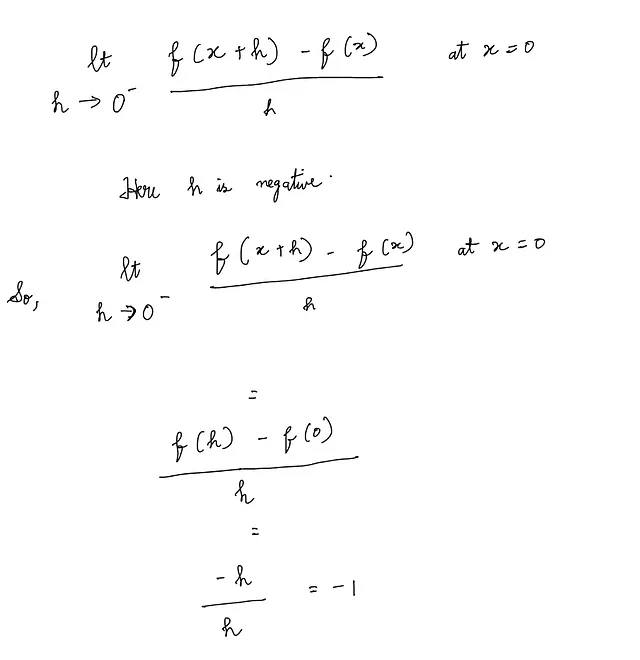
右側の極限:
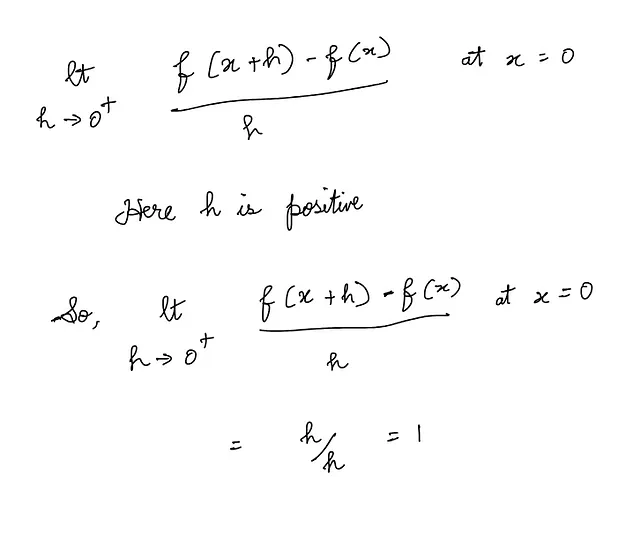
左側の極限は-1、右側の極限は1です。両者は一致しません。したがって、極限に一意な値はなく、存在しません。したがって、f(x) = |x|はx=0で微分可能ではありません。このような関数は、角(またはカスプまたは急な曲がり)を持つと言われます。このような関数は非滑らかです。このような関数の例のグラフは次のようになります:
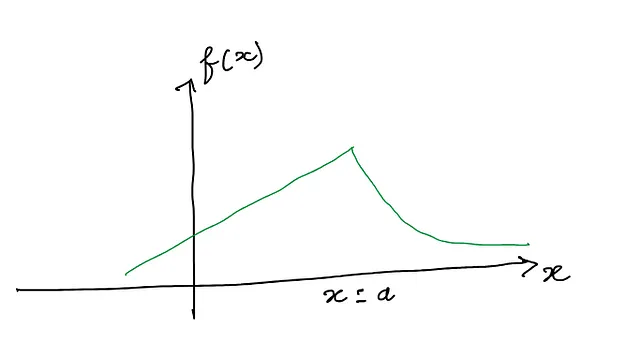
この関数にはx=aの場所に角があります。
以下に示すような不連続な関数は、不連続点では左右の極限が一致しないため、微分不可能です:
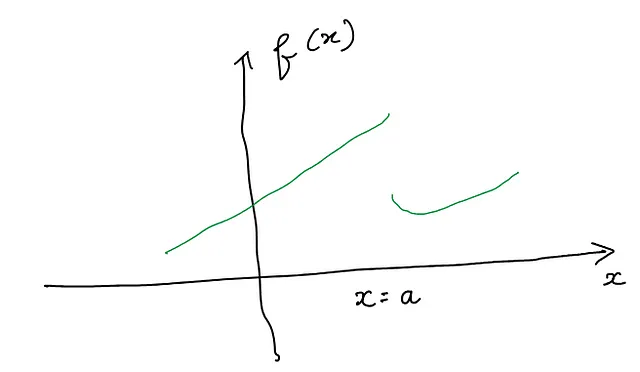
注意:
- 関数が無限の値を取る点も不連続と呼ばれます。
- 関数の値が単一の点の場合も不連続です。以下に示すように、この関数はx=aで値2を取ります:
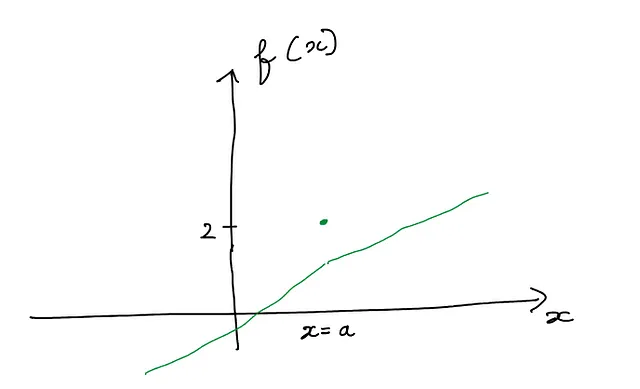
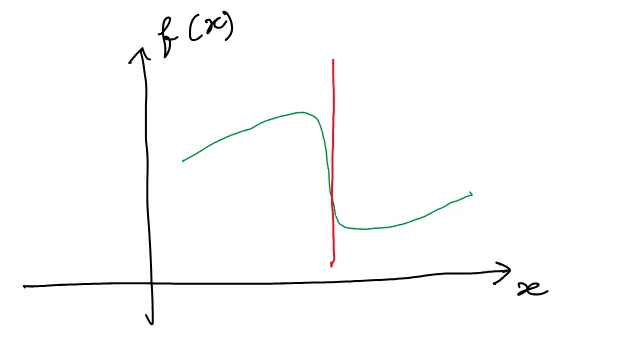
接線が垂直な点で関数は微分不可能です。なぜなら、その点では接線の傾きが未定義(無限大)になるためです。以下にそのような関数の例を示します(赤線はx=aでの接線です):
したがって、関数が微分不可能な3つの種類の点が存在します:
- 角(または尖り、急な曲がり角)
- 不連続(ジャンプ、無限大、点)
- 垂直接線(傾きが未定義)
次の関数が微分不可能な点はどこですか?
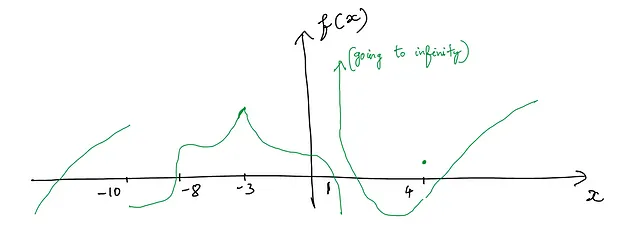
点は次のとおりです:
- 角 -> -3
- 不連続 -> -10、1、4
- 垂直接線 -> -8
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles






