関数の導関数ーそれは何ですか？

関数の導関数ー何ですか？

関数 f(x) の点 x における接線とは何ですか？それは、関数が点 x でのみ接する直線です。他の点 x2（x とは異なる）で関数と交差しません。

関数 f(x) の点 x における導関数とは何ですか？それは、その点での関数の接線の傾きです。

次の関数を考えてみましょう：

• 「ChatGPTのコードインタプリターがついにオープンしました具体的にはどのように動作するのでしょうか？こちらがチュートリアルです」
• 「人工知能 vs 人間の知能：トップ7の違い」
• 「ジェネレーティブAIがプライバシーとセキュリティにおいて現在どのような位置にいるのか」

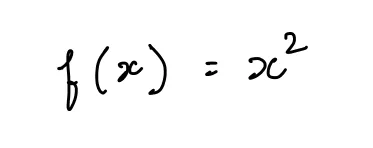
この関数のグラフは次のようになります：

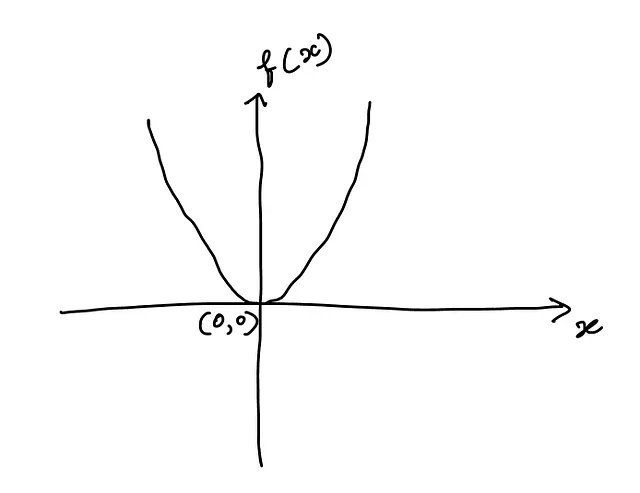
x < 0 の場合、x での関数の接線は次のようになります：

この接線は負の傾きを持ちます。したがって、f(x) の x < 0 における導関数は負です。

x > 0 の場合、x での関数の接線は次のようになります：

この接線は正の傾きを持ちます。したがって、f(x) の x > 0 における導関数は正です。

x = 0 の場合、関数の接線は次のように x 軸と重なります：

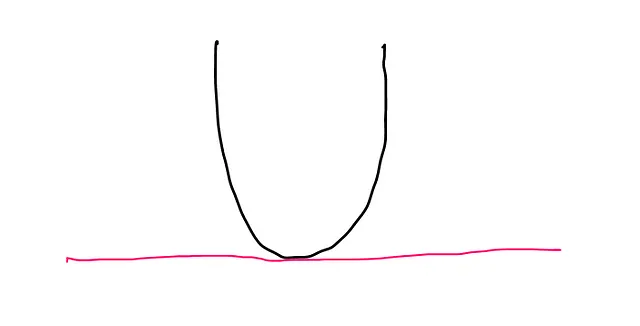
この接線の傾きは 0 です。したがって、f(x) の x = 0 における導関数はゼロです。

なお、x = 0 の場合、接線は以下のようになりません。なぜならば、その直線は関数と 2 点で交差するからです：

関数 f(x) の導関数は数学的に次の極限として定義されます：

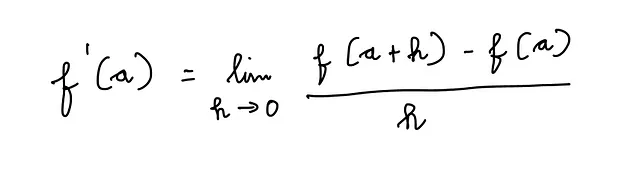
ここで h は無限小の数です。

h が負の方向から 0 に近づくとき（h の負の値に対して）、次の極限の値は次のようになります：

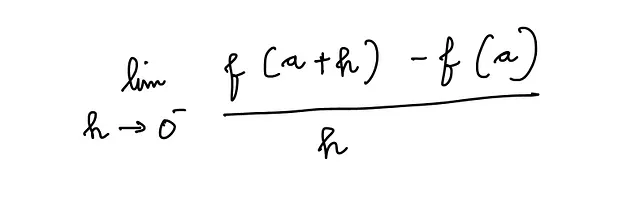
h が正の方向から 0 に近づくとき（h の正の値に対して）、次の極限の値は次のようになります：

導関数は次のように表されます：

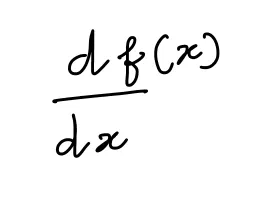
これらの二つの極限は等しくなければなりません。その極限値が導関数です。

ここで x = a における df(x) は：

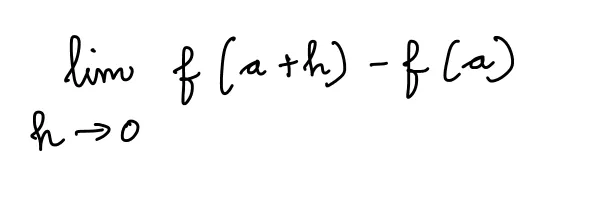
ここで dx は：

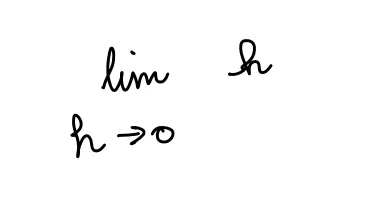
上記の例はすべての x で連続かつ滑らかな関数です。関数の導関数は、連続かつ滑らかな点でのみ存在し、垂直接線が発生しない点で存在します（垂直接線が発生する点では、接線の傾きは無限大です）。導関数は微分とも呼ばれます。

関数には導関数が存在しない点があります。そのような点では関数は微分可能ではありません。今後の投稿でそのような点を見ていきます。

では、これでサインオフします！

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!