重み量子化の概要
重み量子化の概要
8ビット量子化による大規模言語モデルのサイズ削減

大規模言語モデル(LLM)は、計算要件が非常に高いことで知られています。通常、モデルのサイズは、パラメータの数(サイズ)にこれらの値の精度(データ型)を乗じることで計算されます。しかし、メモリを節約するために、量子化というプロセスを用いて低精度のデータ型を使用して重みを保存することができます。
文献では、主に2つの重み量子化技術のファミリーが区別されます:
- 事後トレーニング量子化(PTQ)は、既にトレーニング済みのモデルの重みを再トレーニングせずに、低精度に変換する単純な技術です。実装は容易ですが、PTQは潜在的なパフォーマンスの低下と関連しています。
- 量子化意識トレーニング(QAT)は、事前トレーニングまたはファインチューニングの段階で重み変換プロセスを組み込むことで、モデルのパフォーマンスを向上させます。しかし、QATは計算量が多く、代表的なトレーニングデータが必要とされます。
本記事では、パラメータの精度を下げるためにPTQに焦点を当てます。より具体的な理解を得るために、GPT-2モデルを使用したおもちゃの例に対して単純な手法とより洗練された手法の両方を適用します。
コード全体はGoogle ColabとGitHubで無料で利用できます。
📚 浮動小数点表現の背景
データ型の選択は、必要な計算リソースの量を決定し、モデルの速度と効率に影響を与えます。深層学習のアプリケーションでは、精度と計算パフォーマンスのバランスを取ることが重要であり、高い精度はしばしばより大きな計算要件を意味します。
さまざまなデータ型の中で、浮動小数点数は高い精度で広範囲の値を表現する能力から、深層学習で主に使用されています。通常、浮動小数点数は数値を格納するためにnビットを使用します。これらのnビットは、3つの異なるコンポーネントにさらに分割されます:
- 符号:符号ビットは数値の正負を示します。0は正の数を、1は負の数を表します。
- 指数:指数は、基数(通常は2進数表現の場合は2)のべき乗を表すビットのセグメントです。指数は正または負の値を持つこともでき、非常に大きな値または非常に小さな値を表すことができます。
- 有効桁数/仮数:残りのビットは有効桁数、または仮数として使用されます。これは数値の有効桁を表します。数値の精度は、有効桁数の長さに大きく依存します。
この設計により、浮動小数点数はさまざまな範囲の値を、異なる精度レベルでカバーすることができます。この表現に使用される式は次のとおりです:

これをより良く理解するために、深層学習で最も一般的に使用されるいくつかのデータ型について見てみましょう:float32(FP32)、float16(FP16)、およびbfloat16(BF16)です:
- FP32は32ビットを使用して数値を表現します。符号に1ビット、指数に8ビット、有効桁数に残りの23ビットが使用されます。高精度を提供しますが、FP32の欠点は高い計算およびメモリの使用量です。
- FP16は16ビットを使用して数値を格納します。符号に1ビット、指数に5ビット、有効桁数に10ビットが使用されます。これにより、メモリの使用効率が向上し、計算が加速されますが、範囲と精度が低下するため、数値の不安定性が生じ、モデルの精度に影響を与える可能性があります。
- BF16も16ビットの形式ですが、符号に1ビット、指数に8ビット、有効桁数に7ビットが使用されます。BF16はFP16と比べて表現範囲が広がり、アンダーフローやオーバーフローのリスクが減少します。有効桁数の減少による精度の低下にもかかわらず、BF16は通常モデルのパフォーマンスにほとんど影響を与えず、深層学習タスクにおいて有用な妥協点となります。

機械学習の専門用語では、FP32はしばしば「フルプレシジョン」(4バイト)と呼ばれ、BF16とFP16は「ハーフプレシジョン」(2バイト)と呼ばれます。しかし、1バイトで重みを格納することはできるのでしょうか?その答えはINT8データ型です。INT8データ型は、256個の異なる値を格納することができる8ビットの表現です。次のセクションでは、FP32の重みをINT8形式に変換する方法について見ていきます。
🔰 単純な8ビット量子化
このセクションでは、2つの量子化技術を実装します。1つは絶対値最大値(absmax)量子化であり、もう1つはゼロポイント量子化です。どちらの場合でも、FP32テンソルX(元の重み)をINT8テンソルX_quant(量子化された重み)にマッピングすることが目標です。
absmax量子化では、元の数値はテンソルの絶対最大値で割られ、スケーリングファクター(127)で乗算され、入力を範囲[-127, 127]にマッピングします。元のFP16値を取得するには、INT8の数値を量子化ファクターで割り、四捨五入による精度の損失を認識する必要があります。

例えば、絶対最大値が3.2の場合、重み0.1はround(0.1 × 127/3.2) = 4に量子化されます。逆量子化すると、4 × 3.2/127 = 0.1008となり、誤差は0.008です。以下は対応するPythonの実装です。
import torchdef absmax_quantize(X): # スケールを計算 scale = 127 / torch.max(torch.abs(X)) # 量子化 X_quant = (scale * X).round() # 逆量子化 X_dequant = X_quant / scale return X_quant.to(torch.int8), X_dequantゼロポイント量子化では、入力の分布が非対称であることを考慮することができます。たとえば、ReLU関数の出力(正の値のみ)を考慮する場合に便利です。入力値は、最大値と最小値の差で割られた値の範囲(255)でスケーリングされます。この分布は、ゼロポイントによって範囲[-128, 127]にマッピングされます(absmaxと比べて1つの値が追加されていることに注意してください)。まず、スケールファクターとゼロポイントの値を計算します。

次に、これらの変数を使用して重みを量子化または逆量子化することができます。

例を挙げて説明しましょう。最大値が3.2、最小値が-3.0の場合、スケールは255/(3.2 + 3.0) = 41.13、ゼロポイントは-round(41.13 × -3.0) – 128 = 123 -128 = -5となります。したがって、0.1の重みはround(41.13 × 0.1 -5) = -1に量子化されます。これは、absmaxを使用した場合に得られた以前の値とは非常に異なります(4 vs -1)。

Pythonの実装は非常に簡単です。
def zeropoint_quantize(X): # 値の範囲(分母)を計算する x_range = torch.max(X) - torch.min(X) x_range = 1 if x_range == 0 else x_range # スケールを計算する scale = 255 / x_range # ゼロポイントでシフトする zeropoint = (-scale * torch.min(X) - 128).round() # 入力をスケールして四捨五入する X_quant = torch.clip((X * scale + zeropoint).round(), -128, 127) # デクオンタイズする X_dequant = (X_quant - zeropoint) / scale return X_quant.to(torch.int8), X_dequant完全なおもちゃの例に頼る代わりに、transformers ライブラリを使用して実際のモデルにこれらの2つの関数を適用できます。
GPT-2 のモデルとトークナイザをロードすることから始めます。これは非常に小さなモデルであり、量子化する必要はありませんが、このチュートリアルには十分です。まず、モデルのサイズを観察して、後で比較し、8ビットの量子化によるメモリの節約を評価します。
!pip install -q bitsandbytes>=0.39.0!pip install -q git+https://github.com/huggingface/accelerate.git!pip install -q git+https://github.com/huggingface/transformers.git
from transformers import AutoModelForCausalLM, AutoTokenizerimport torchtorch.manual_seed(0)# 現在はCPUをデバイスに設定するdevice = 'cpu'# モデルとトークナイザをロードするmodel_id = 'gpt2'model = AutoModelForCausalLM.from_pretrained(model_id).to(device)tokenizer = AutoTokenizer.from_pretrained(model_id)# モデルのサイズを出力するprint(f"モデルのサイズ: {model.get_memory_footprint():,} バイト")
モデルのサイズ: 510,342,192 バイトGPT-2 モデルのサイズはおよそ 487MB(FP32)です。次のステップは、ゼロポイントと absmax の量子化を使用して重みを量子化することです。以下の例では、GPT-2 の最初のアテンション層にこれらの技術を適用して結果を確認します。
# 最初の層の重みを抽出するweights = model.transformer.h[0].attn.c_attn.weight.dataprint("元の重み:")print(weights)# absmax 量子化を使用して層を量子化するweights_abs_quant, _ = absmax_quantize(weights)print("\nabsmax 量子化された重み:")print(weights_abs_quant)# ゼロポイント 量子化を使用して層を量子化するweights_zp_quant, _ = zeropoint_quantize(weights)print("\nゼロポイント 量子化された重み:")print(weights_zp_quant)
元の重み:tensor([[-0.4738, -0.2614, -0.0978, ..., 0.0513, -0.0584, 0.0250], [ 0.0874, 0.1473, 0.2387, ..., -0.0525, -0.0113, -0.0156], [ 0.0039, 0.0695, 0.3668, ..., 0.1143, 0.0363, -0.0318], ..., [-0.2592, -0.0164, 0.1991, ..., 0.0095, -0.0516, 0.0319], [ 0.1517, 0.2170, 0.1043, ..., 0.0293, -0.0429, -0.0475], [-0.4100, -0.1924, -0.2400, ..., -0.0046, 0.0070, 0.0198]])absmax 量子化された重み:tensor([[-21, -12, -4, ..., 2, -3, 1], [ 4, 7, 11, ..., -2, -1, -1], [ 0, 3, 16, ..., 5, 2, -1], ..., [-12, -1, 9, ..., 0, -2, 1], [ 7, 10, 5, ..., 1, -2, -2], [-18, -9, -11, ..., 0, 0, 1]], dtype=torch.int8)ゼロポイント 量子化された重み:tensor([[-20, -11, -3, ..., 3, -2, 2], [ 5, 8, 12, ..., -1, 0, 0], [ 1, 4, 18, ..., 6, 3, 0], ..., [-11, 0, 10, ..., 1, -1, 2], [ 8, 11, 6, ..., 2, -1, -1], [-18, -8, -10, ..., 1, 1, 2]], dtype=torch.int8)オリジナル(FP32)と量子化(INT8)の値の違いは明確ですが、absmaxとゼロポイントの重みの違いはより微妙です。この場合、入力は-1の値でシフトされているように見えます。これは、この層の重み分布がかなり対称的であることを示唆しています。
私たちは、GPT-2のすべてのレイヤー(線形レイヤー、アテンションレイヤーなど)を量子化し、2つの新しいモデルmodel_absとmodel_zpを作成することで、これらの技術を比較することができます。正確には、実際には元の重みを非量子化された重みで置き換えることになります。これには2つの利点があります。1つは、重みの分布を比較することができることです(同じスケール)。2つ目は、実際にモデルを実行できることです。
実際には、PyTorchではINT8の行列乗算をデフォルトで許可していません。実際のシナリオでは、モデルを実行するためにそれらを非量子化する(例えばFP16で)が、INT8として保存することがあります。次のセクションでは、この問題を解決するためにbitsandbytesライブラリを使用します。
import numpy as npfrom copy import deepcopy# 元の重みを保存weights = [param.data.clone() for param in model.parameters()]# 量子化するためのモデルを作成model_abs = deepcopy(model)# すべてのモデルの重みを量子化weights_abs = []for param in model_abs.parameters(): _, dequantized = absmax_quantize(param.data) param.data = dequantized weights_abs.append(dequantized)# 量子化するためのモデルを作成model_zp = deepcopy(model)# すべてのモデルの重みを量子化weights_zp = []for param in model_zp.parameters(): _, dequantized = zeropoint_quantize(param.data) param.data = dequantized weights_zp.append(dequantized)モデルが量子化されたので、このプロセスの影響を確認したいと思います。直感的には、量子化された重みが元の重みに近いことを確認したいと思います。重みの分布をプロットすることで視覚的に確認する方法があります。量子化が損失を伴う場合、重みの分布は大きく変わるでしょう。
次の図は、この比較を示しており、青いヒストグラムが元の(FP32)の重みを、赤いヒストグラムが量子化(INT8)した重みを表しています。非常に高い絶対値を持つ外れ値のため、このプロットは-2から2までしか表示されません(後述)。
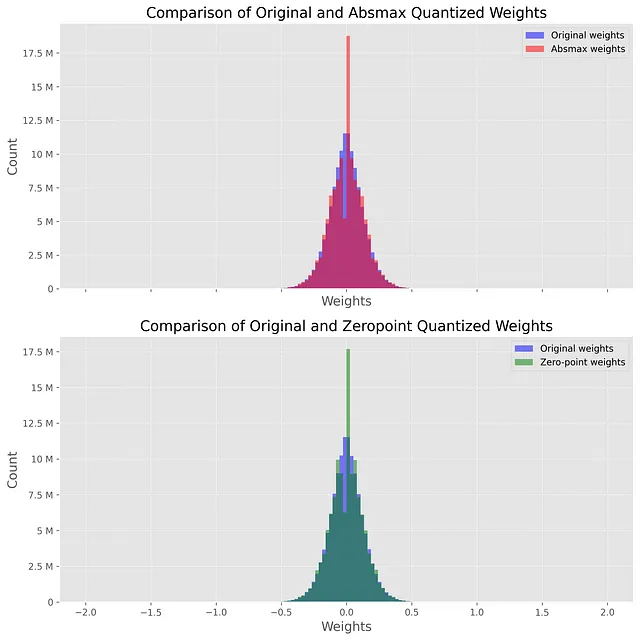
両方のプロットは非常に似ており、0周りに驚くほどのスパイクがあります。このスパイクは、量子化がかなり損失を伴うことを示しています。なぜなら、プロセスを逆にしても元の値を出力しないからです。これは特にabsmaxモデルに当てはまり、0周りに低い谷と高いスパイクが表示されます。
次に、オリジナルモデルと量子化モデルのパフォーマンスを比較しましょう。この目的のために、generate_text()関数を定義して、トップ-Kサンプリングで50トークンを生成します。
def generate_text(model, input_text, max_length=50): input_ids = tokenizer.encode(input_text, return_tensors='pt').to(device) output = model.generate(inputs=input_ids, max_length=max_length, do_sample=True, top_k=30, pad_token_id=tokenizer.eos_token_id, attention_mask=input_ids.new_ones(input_ids.shape)) return tokenizer.decode(output[0], skip_special_tokens=True)# オリジナルモデルと量子化モデルでテキストを生成original_text = generate_text(model, "I have a dream")absmax_text = generate_text(model_abs, "I have a dream")zp_text = generate_text(model_zp, "I have a dream")print(f"オリジナルモデル:\n{original_text}")print("-" * 50)print(f"Absmaxモデル:\n{absmax_text}")print("-" * 50)print(f"Zeropointモデル:\n{zp_text}")オリジナルモデル:私は夢を持っていますが、それは私が将来実現できると信じている夢です。私は母を愛していますが、私の家族はそれほど強くないと言われたことがあります。そして、私は
他の出力よりもどれがより意味をなすかを見ようとする代わりに、各出力のパープレキシティを計算して量化することができます。これは言語モデルを評価するために使用される一般的な指標であり、シーケンス内の次のトークンを予測するモデルの不確実性を測定します。この比較では、スコアが低いほどモデルが優れているという一般的な仮定を行っています。実際には、パープレキシティが高い文も正しい場合があります。
文は短いため、コンテキストウィンドウの長さなどの詳細を考慮する必要がないため、最小の関数を使用して実装します。
def calculate_perplexity(model, text): # テキストをエンコードする encodings = tokenizer(text, return_tensors='pt').to(device) # input_idsとtarget_idsを定義する input_ids = encodings.input_ids target_ids = input_ids.clone() with torch.no_grad(): outputs = model(input_ids, labels=target_ids) # 損失の計算 neg_log_likelihood = outputs.loss # パープレキシティの計算 ppl = torch.exp(neg_log_likelihood) return pplppl = calculate_perplexity(model, original_text)ppl_abs = calculate_perplexity(model_abs, absmax_text)ppl_zp = calculate_perplexity(model_zp, absmax_text)print(f"元のパープレキシティ: {ppl.item():.2f}")print(f"Absmaxパープレキシティ: {ppl_abs.item():.2f}")print(f"Zeropointパープレキシティ: {ppl_zp.item():.2f}")元のモデルのパープレキシティは、他の2つよりもわずかに低いことがわかります。一つの実験では信頼性があまりありませんが、このプロセスを複数回繰り返して各モデルの違いを見ることができます。理論的には、ゼロポイント量子化はabsmaxよりわずかに優れているはずですが、計算コストが高くなります。
この例では、量子化技術を全体のレイヤー(テンソルごと)に適用しました。しかし、異なる粒度レベルで適用することもできます。全体のモデルを一度に量子化すると性能が著しく低下しますが、個々の値を量子化すると大きなオーバーヘッドが発生します。実際には、行と列の中の値の変動性を考慮するベクトルワイズ量子化が好まれることが多いです。
しかし、ベクトルワイズ量子化でも外れ値の問題は解決されません。外れ値は、モデルが一定のスケール(6.7Bパラメーター以上)に達したときに、すべてのトランスフォーマーレイヤーに現れる極端な値(負の値または正の値)です。これは問題です、なぜなら単一の外れ値が他のすべての値の精度を低下させる可能性があるからです。ただし、これらの外れ値の特徴を破棄することは選択肢ではありません。なぜなら、モデルの性能が大幅に低下する可能性があるからです。
🔢 LLM.int8()による8ビット量子化
LLM.int8()は、Dettmersらによって導入された外れ値問題の解決策です。これは、ベクトルワイズ(absmax)量子化スキームを利用し、混合精度量子化を導入しています。これは、外れ値の特徴をFP16形式で処理して精度を保持し、他の値をINT8形式で処理します。外れ値は全体の値の約0.1%を占めるため、これによりLLMのメモリ使用量がほぼ2倍に削減されます。

LLM.int8()は、行列の乗算演算を次の3つの主要なステップで行います:
- カスタムのしきい値を使用して外れ値を含む入力隠れ状態Xから列を抽出します。
- 外れ値をFP16で、外れ値以外の値をINT8でベクトルワイズ量子化(隠れ状態Xに対して行ごとに、重み行列Wに対して列ごとに)を使用して行列の乗算を行います。
- 非外れ値の結果をデクォンタイズ(INT8からFP16)し、外れ値の結果に追加して、完全な結果をFP16で取得します。

このアプローチは、8ビットの精度が制限されており、大きな値を持つベクトルを量子化する際に大きな誤差を生じる可能性があるため必要です。これらの誤差は、複数の層を通過する際に増幅する傾向があります。
私たちは、Hugging Faceエコシステムにbitsandbytesライブラリが統合されているおかげで、このテクニックを簡単に使用することができます。モデルをロードする際にload_in_8bit=Trueを指定するだけで使用できます(GPUも必要です)。
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')model_int8 = AutoModelForCausalLM.from_pretrained(model_id, device_map='auto', load_in_8bit=True, )print(f"モデルのサイズ:{model_int8.get_memory_footprint():,} バイト")
モデルのサイズ:176,527,896 バイトこの追加のコード行により、モデルのサイズは約3倍小さくなります(168MB vs. 487MB)。さらに、元の重みと量子化された重みの分布を比較することもできます:

この場合、-2、-1、0、1、2などのスパイクが見られます。これらの値はINT8形式で格納されたパラメータに対応しています(外れ値ではありません)。model_int8.parameters()を使用してモデルの重みを表示することで検証できます。
この量子化されたモデルを使用してテキストを生成し、元のモデルと比較することもできます。
# 量子化モデルでテキストを生成text_int8 = generate_text(model_int8, "I have a dream")print(f"元のモデル:\n{original_text}")print("-" * 50)print(f"LLM.int8()モデル:\n{text_int8}")
元のモデル:I have a dream, and it is a dream I believe I would get to live in my future. I love my mother, and there was that one time I had been told that my family wasn't even that strong. And then I got the--------------------------------------------------LLM.int8()モデル:I have a dream. I don't know what will come of it, but I am going to have to look for something that will be right. I haven't thought about it for a long time, but I have to try to get that thing再度述べると、最適な出力を判断するのは難しいですが、パープレキシティの指標に頼ることができます(おおよその答えが得られます)。
print(f"パープレキシティ(元のモデル): {ppl.item():.2f}")ppl = calculate_perplexity(model_int8, text_int8)print(f"パープレキシティ(LLM.int8()): {ppl.item():.2f}")
パープレキシティ(元のモデル): 15.53パープレキシティ(LLM.int8()): 7.93この場合、量子化されたモデルのパープレキシティは元のモデルの2倍低くなっています。一般的にはそうではありませんが、この量子化技術は非常に競争力があることを示しています。実際、LLM.int8()の著者は、パフォーマンスの低下が非常に低く(1%未満)無視できるレベルであることを示しています。ただし、計算コストは増えます。LLM.int8()は、大きなモデルに対して約20%遅くなります。
結論
この記事では、最も人気のある重み量子化技術の概要を説明しました。浮動小数点表現の理解を得た後、8ビット量子化のための2つの技術、absmaxおよびゼロポイント量子化を紹介しました。ただし、これらの制限は、外れ値の処理に関して特に問題があり、LLM.int8()が生まれました。この技術は、モデルのパフォーマンスも保持します。このアプローチは、重み量子化の進歩を示し、外れ値の適切な対処の重要性を明らかにしています。
次の記事では、GPTQ重み量子化技術を詳しく探求します。この技術はFrantarらによって紹介され、わずか4ビットしか使用せず、重み量子化の分野での重要な進展を示しています。AutoGPTQライブラリを使用してGPTQを実装する包括的なガイドを提供します。
LLMに関するより詳細な技術コンテンツに興味がある場合は、Twitterで私をフォローしてください:@maximelabonne
参考文献
- T. Dettmers、M. Lewis、Y. Belkada、L. Zettlemoyer、「LLM.int8():スケールでのトランスフォーマーのための8ビット行列乗算」。2022。
- Y. Beldaka、T. Dettmers、「8ビット行列乗算の優しい導入」、Hugging Face Blog(2022)。
- A. Gholami、S. Kim、Z. Dong、Z. Yao、M. W. Mahoney、K. Keutzer、「効率的なニューラルネットワーク推論のための量子化手法の調査」。2021。
- H. Wu、P. Judd、X. Zhang、M. Isaev、P. Micikevicius、「ディープラーニング推論のための整数量子化:原理と実証評価」。2020。
- Lilian Weng、「大規模トランスフォーマーモデルの推論最適化」、Lil’Log(2023)。
- Kamil Czarnogorski、「ローカル大規模言語モデル」、Int8(2023)。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
