「適応遺伝的二次方程式を使用した四次根の計算」
適応遺伝的二次方程式で四次根を計算する

遺伝子二次関数による四次関数の設計の簡素化
以前の四次根解法の記事では、対象の関数に合わせた二次関数を使用して解法を開発しました。
この記事では、同様の方法論を採用していますが、係数D(x)の値が簡約された四次関数y=x⁴+Cx²+Dx+Eのために適応できる「ワンサイズフィットオール」の遺伝子二次方程式を使用し、関数の変更を効率的かつグラフィカルに直感的に行います。この二次関数は以下の形式を取ります。
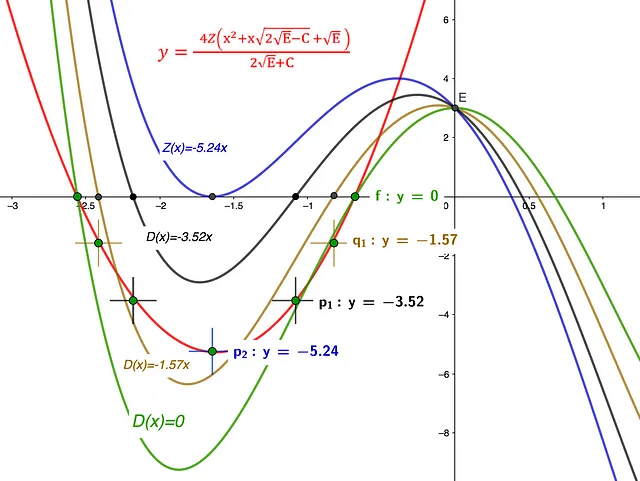
下記のグラフ1の赤い線で示されているように、Eは通常の四次定数であり、Cはx²の係数です。4つの根のxの係数としてZを指定します。青で示される制限関数y=x⁴+Cx²+Zx+E。
対称的な遺伝子四次関数y=x⁴+Cx²+EであるBig Wは、緑で示されています。
負のx係数Dをもつすべての関数は、Big Wのルート範囲内に根を持ちます。
グラフ1
黒と金の内部関数の根を示すラインx=Rtが、それぞれのx係数のラインy=Dと交差している様子が示されています。
四次根
赤い二次関数は、制限値ZからD=0までの交点に密接にフィットします。
四次関数y=x⁴+Cx²+Dx+Eの根は、以下のように遺伝子二次関数との交点であるy=Dの線によって近似されます。
遺伝子二次関数
ヘッドラインのグラフで点線で示される遺伝子二次関数は、x²の係数A=1として、X-Yグリッド内のx<0で以下のように示されます。
その根は、それぞれの特定のBig Wの親の根と等しく、”乗数”Mによって採用された後、さまざまな四次関数のy=Dとの交点は、それらの四次関数の根に対して良好な近似値を提供します。
遺伝子二次関数の適応
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles






