車両ルーティング問題 正確な解法とヒューリスティック解法
車両ルーティング問題の解法
Pythonを使用して複雑なルーティング問題を解決する方法を理解する
車両ルーティング問題(VRP)は、一連の顧客にサービスを提供するために車両フリートが実行する最適なルートのセットを決定することを目的としています。そのいくつかの応用と組み合わせ的な側面のため、これは運用調査と数値最適化の中で最も研究されている問題の1つです。
容量制約付き車両ルーティング問題(CVRP)は、限られた積載容量と可能な持続時間/距離制約を導入するため、最も一般的な変種の1つです。その他の通常の変種には、複数のデポ、異種フリート、ピックアップと配達、および時間枠制約が含まれます。
これらの問題の組み合わせ的な側面は、15つのポイントの単純なセットを考慮すると、それらを接続する6 × 10¹¹の可能な経路が存在することを示しています(Dantzig&Ramser、1959年)。したがって、数十年にわたる計算とアルゴリズムの研究の進歩がなければ、いくつかの実世界の応用は実用的ではありませんでした。Branch-Cut-and-Priceアルゴリズムは、数百の顧客を持つCVRPインスタンスの最適性を証明することができました(Fukasawa et al.、2006年;Pecin et al.、2017年)、および最先端のメタヒューリスティクスとローカルサーチ技術を組み合わせた手法は、これらのインスタンスに対して数秒以内に(時には最適な)解を提供することができます(Vidal et al.、2012年;Vidal、2022年)。
この記事では、積載(および所要時間)制約を持つ容量制約付き車両ルーティング問題を紹介し、混合整数計画法(MIP)と専門的な(メタ)ヒューリスティックアルゴリズムを使用して解決します。最初の部分では、Python AML PyomoとHiGHSソルバーを使用し、2番目の部分ではGoogle OR Toolsパッケージを使用します。
- 「EU AI Actについて今日関心を持つべき理由」
- Pythonコードの品質向上ガイド:データサイエンティストのためのガイド
- 「Meetupsからメンタリングまで データサイエンティストとしてのネットワーキングの方法」
問題の理論的な側面よりも実世界の応用に関心がある読者は、MIPセクションを素早くスキャンし、専門的な(メタ)ヒューリスティックと有用な拡張セクションにより関心を向けることができます。
数値最適化に詳しくないが、MIPの形式を詳細に理解したいと思っている読者は、この記事の前の投稿である線形プログラミングとブランチ&バウンド法について調べてから、この記事を読むと役に立つかもしれません。
いつものように、このgitリポジトリで完全なコードを見つけることができます。
それでは、さっそく始めましょう!
混合整数計画法
このセクションで提示される数学的な形式は、Toth&Vigo(2002年)が「三指標車両フロー形式」として参照しているモデルで提示されている同じ方程式を使用します。
ノードのセットV(需要とデポ)と車両のセットKを考えます。ノードインデックスには小文字のiとjを使用し、車両インデックスには小文字のkを使用します。このモデルは非対称の場合も有効なため、ノードは完全な有向グラフG(V、A)の一部であると仮定しましょう。この問題では、0でインデックス付けされた単一のデポノードがあり、すべての車両には同じ容量Qがあります。次のような2つのグループの決定変数を考えます。
- x_{i, j, k}:ノードiからノードjへのアクティブなアークを示すバイナリ変数。
- y_{i, k}:ノードiの需要が車両kによって満たされることを示すバイナリ変数。
アクティブなアークに関連するコスト値を最小化することを目的とするとします。合計所要時間または距離が一般的な例です。アークi、jを通過するコストをcᵢⱼとします。目的関数は次のように述べることができます。
また、次の制約も含める必要があります。
- 各顧客iは1回だけ訪問されるため、それに始まるアクティブなアークとそれに到着するアークが1つずつ存在することを保証する制約。
- 車両kによってインデックス付けられた任意のアーク変数がノードiに入るか出る場合、このノードの需要qは車両kに割り当てられる制約。
- 車両に割り当てられた総需要が容量Qを超えない制約。
- |K|個のノードがデポで始まり、デポで到着する制約。
- サブツアーは存在しない…ただし、サブツアーの数は開始時に列挙するには可能性がありすぎます。どのように行うかについて詳しく説明します。
通常のPythonチュートリアルと同様に、このセクションで使用されるライブラリをインポートして、実際の手順を開始しましょう:
import timefrom itertools import cycleimport numpy as npfrom scipy.spatial.distance import pdist, squareformimport matplotlib.pyplot as pltimport matplotlib as mplimport networkx as nximport pyomo.environ as pyofrom pyomo.contrib.appsi.solvers.highs import Highsそして、Nの需要ノードを持つランダムな問題をインスタンス化しましょう。この例では、デポノードは最初のノード(インデックス0)として想定されているため、対応する需要もゼロになるようにします。
np.random.seed(42) # 結果は常に同じになるようにするN = 10demands = np.random.randint(1, 10, size=N)demands[0] = 0capacity = 15n_vehicles = 4coordinates = np.random.rand(N, 2)distances = squareform(pdist(coordinates, metric="euclidean"))distances = np.round(distances, decimals=4) # 数値誤差を回避するために四捨五入必要な車両の数はBin Packing Problemを使用して計算することができます。完全なソースコードには、これを実行する方法の例も含まれています。
pyomoで問題をモデル化するためには2つのアプローチがあります:抽象モデルと具体モデルです。最初のアプローチでは、問題の代数的な式がいくつかのデータ値が供給される前に定義されます。一方、2番目のアプローチでは、モデルのインスタンスが要素が定義されると同時に作成されます。これらのアプローチについては、ライブラリのドキュメントやBynum et al.(2021)の書籍で詳細を確認できます。本記事では、具体モデルの形式を採用します。
model = pyo.ConcreteModel()需要ノードV、アークA、および車両Kのセットをインスタンス化しましょう。元の数学的な定式化と同様に、デポノードもノードVのセットに含まれていることに注意してください。
model.V = pyo.Set(initialize=range(len(demands)))model.A = pyo.Set(initialize=[(i, j) for i in model.V for j in model.V if i != j])model.K = pyo.Set(initialize=range(n_vehicles))そして、容量、需要負荷、およびアークコストのパラメータを設定します。
model.Q = pyo.Param(initialize=capacity)model.q = pyo.Param(model.V, initialize={i: d for (i, d) in enumerate(demands)})model.c = pyo.Param(model.A, initialize={(i, j): distances[i, j] for (i, j) in model.A})以前にリストされた制約も含める必要があります。まず、通常のPyomoのシグネチャを使用してそれらを実装しましょう:function(model, *domain)。
def arcs_in(model, i): if i == model.V.first(): return sum(model.x[:, i, :]) == len(model.K) else: return sum(model.x[:, i, :]) == 1.0def arcs_out(model, i): if i == model.V.first(): return sum(model.x[i, :, :]) == len(model.K) else: return sum(model.x[i, :, :]) == 1.0def vehicle_assignment(model, i, k): return sum(model.x[:, i, k]) == model.y[i, k]def comp_vehicle_assignment(model, i, k): return sum(model.x[i, :, k]) == model.y[i, k]def capacity_constraint(model, k): return sum(model.y[i, k] * model.q[i] for i in model.V) <= model.Qそして、これらをモデルに組み込みましょう。
model.arcs_in = pyo.Constraint(model.V, rule=arcs_in)model.arcs_out = pyo.Constraint(model.V, rule=arcs_out)model.vehicle_assignment = pyo.Constraint(model.V, model.K, rule=vehicle_assignment)model.comp_vehicle_assignment = pyo.Constraint(model.V, model.K, rule=comp_vehicle_assignment)model.capacity_constraint = pyo.Constraint(model.K, rule=capacity_constraint)まだ部分巡回路排除制約を含めていませんが、これらの制約を列挙することは、中程度のサイズのインスタンスでも非常に大きくなる可能性があります。代わりに、解決手順では、新しい解がサブツアーを生成することが確認された場合にのみ、再帰的に部分巡回路排除制約を追加します。商用ソルバーでは、これらは「遅延制約」と呼ばれ、コールバックを介して直接ソルバーに組み込むことができます。
まず、サブツアー、残りのノード、サブツアーからのノード、および車両が与えられた場合に、以前に述べた数学的な定式化に対応するPyomo式を返す関数を作成しましょう。また、解決策の進行に従って新しい要素を含めるために、ConstraintListを含めましょう。
def subtour_elimination(model, S, Sout, h, k): nodes_out = sum(model.x[i, j, k] for i in S for j in Sout) return model.y[h, k] <= nodes_outmodel.subtour_elimination = pyo.ConstraintList()存在する場合、解決策に基づいて生成されたサブツアーを返すいくつかの関数を作成する必要があります。そのために、find_arcs関数を使用してモデル内のアクティブなアークのリストを作成します。このリストは、NetworkxのDiGraphクラスを使用して不完全な有向グラフを作成するために使用されます。そして、find_subtours関数は接続されたコンポーネントのセットのリストを返す必要があります。
def find_arcs(model): arcs = [] for i, j in model.A: for k in model.K: if np.isclose(model.x[i, j, k].value, 1): arcs.append((i, j)) return arcsdef find_subtours(arcs): G = nx.DiGraph(arcs) subtours = list(nx.strongly_connected_components(G)) return subtours私たちの目標は、デポノードを含まない接続されたコンポーネントのグループを排除することです。したがって、次のステップでは、セットのリストをイテレートする関数を作成し、コンポーネントのセットがデポノードを含まない場合に新しい制約を追加します。これには、ConstraintListクラスのaddメソッドが使用されます。
def eliminate_subtours(model, subtours): proceed = False for S in subtours: if 0 not in S: proceed = True Sout = {i for i in model.V if i not in S} for h in S: for k in model.K: model.subtour_elimination.add( subtour_elimination(model, S, Sout, h, k) ) return proceedそして、現在の解決策にサブツアーが存在するかどうかを確認し、存在する場合はそれらを排除するための新しい制約を追加する手順を反復的に実行し、MIPを解決する手順を提案するために必要なすべての準備が整いました。そうでなければ、見つかった解決策は最適です。
def solve_step(model, solver): sol = solver.solve(model) arcs = find_arcs(model) subtours = find_subtours(arcs) time.sleep(0.1) proceed = eliminate_subtours(model, subtours) return sol, proceed def solve(model, solver): proceed = True while proceed: sol, proceed = solve_step(model, solver) return solさて、ソルバーをインスタンス化し、モデルを解決しましょう。HighsソルバーはPyomoで利用可能です(インポートを確認してください)、highspyパッケージがインストールされている場合に使用できます。したがって、pip install highspyを実行してください。
solver = Highs()solver.highs_options = { "log_file": "Highs.log", "mip_heuristic_effort": 0.2, "mip_detect_symmetry": True, "mip_rel_gap": 1e-6,}solution = solve(model, solver)ツアーを見つけるためのもう一つの関数があり、結果をプロットする準備が整いました。
def find_tours(model): tours = [] for k in model.K: node = 0 tours.append([0]) while True: for j in model.V: if (node, j) in model.A: if np.isclose(model.x[node, j, k].value, 1): node = j tours[-1].append(node) break if node == 0: break return tours
合計10ノードの小さなインスタンスに対する素晴らしい結果です。ただし、この小さなインスタンスでも、ソルバーはほぼ30秒かかり、より多くの需要点がある場合には複雑さが著しく増加します。幸いなことに、大型のインスタンスに対して短い計算時間で良質な解を見つけるための専門的なアルゴリズムが公開されています。次のセクションでそれらを見てみましょう。
専門化された (メタ)ヒューリスティクス
多くの年月をかけて、VRPの異なるバリエーションに対していくつかの専門的な (メタ)ヒューリスティクスが提案されてきました。これらのほとんどは、与えられた解に対してさまざまな摂動を試し、そのコストを順次改善するために局所探索アルゴリズムに強く依存しています。与えられた近傍でさらなる改善が不可能になるまで、コストを改善し続けます。Google Or Toolsを使用する場合、私たちは構築的なアルゴリズムに関連する局所探索手法を使用します。
このセクションでは、RochatとTaillard(1995)のインスタンス150dを使用します。そのデータはCVRPLIBから取得されました。このインスタンスには150人の顧客と1つのデポのノードがありますので、以前に紹介されたMIP戦略を使用して解決することはできません。
まず、使用するライブラリをインポートして始めましょう。
from itertools import cycleimport numpy as npimport pandas as pdfrom scipy.spatial.distance import pdist, squareformimport matplotlib.pyplot as pltimport matplotlib as mplfrom ortools.constraint_solver import routing_enums_pb2from ortools.constraint_solver import pywrapcpそして、各ノードの座標と需要を含むファイルから問題データを読み込みましょう。
dataset = pd.read_csv("./data/tai150d.csv", index_col=0)coordinates = dataset.loc[:, ["x", "y"]]demands = dataset.d.valuescapacity = 1874n_vehicles = 15N = coordinates.shape[0]distances = squareform(pdist(coordinates, metric="euclidean"))distances = np.round(distances, decimals=4)OR Tools VRPソルバーを使用するための最初のステップは、ルーティングマネージャーとモデルをインスタンス化することです。
# ルーティングインデックスマネージャーを作成:ノード数、車両数、デポノードmanager = pywrapcp.RoutingIndexManager( N, n_vehicles, 0)# ルーティングモデルを作成routing = pywrapcp.RoutingModel(manager)次に、アーク/エッジおよびノードに関連する次元を定量化するためのコールバックを含めます。ルーティングインスタンスのRegisterTransitCallbackメソッドは、アーク/エッジに関連する任意の次元を定量化するために使用できます。RegisterUnaryTransitCallbackメソッドは、ノードに関連する値を定量化することができます。
# アーク/エッジに関連するコールバックに対しても同じことが有効ですdef distance_callback(from_index, to_index): from_node = manager.IndexToNode(from_index) to_node = manager.IndexToNode(to_index) return distances[from_node, to_node]transit_callback_index = routing.RegisterTransitCallback(distance_callback)# ノードに関連するコールバックに対しても同じことが有効ですdef demand_callback(from_index): from_node = manager.IndexToNode(from_index) return demands[from_node]demand_callback_index = routing.RegisterUnaryTransitCallback(demand_callback)さて、先に定義したdemand_callback_indexを使用して容量制約を追加します。同じ構文を使用して、所要時間制約も定義することができます。また、ルーティングモデルは異種のフリートを扱うことができるため、第3引数に値のリストを渡す必要があります。
# 車両に関連する制約は同じ引数を取れますrouting.AddDimensionWithVehicleCapacity( demand_callback_index, 0, # null capacity slack [capacity,] * n_vehicles, # vehicle maximum capacities (list for each vehicle) True, # start cumul to zero 'Capacity')同様に、目的関数の定義もコールバックを主な引数として受け取ります。この例では、transit_callback_indexで定義された距離を最小化します。
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)最後に、ソルバーパラメータを定義し、モデルを解決します。
# ヒューリスティック戦略を設定search_parameters = pywrapcp.DefaultRoutingSearchParameters()search_parameters.first_solution_strategy = ( routing_enums_pb2.FirstSolutionStrategy.CHRISTOFIDES)search_parameters.local_search_metaheuristic = ( routing_enums_pb2.LocalSearchMetaheuristic.GUIDED_LOCAL_SEARCH)search_parameters.time_limit.FromSeconds(300)# 問題を解決solution = routing.SolveWithParameters(search_parameters)次のコードは、解決策で使用されたルートを抽出するために使用できます。
tours = []for vehicle_id in range(n_vehicles): index = routing.Start(vehicle_id) tours.append([]) while not routing.IsEnd(index): node_index = manager.IndexToNode(index) previous_index = index index = solution.Value(routing.NextVar(index)) tours[-1].append(node_index) else: node_index = manager.IndexToNode(index) tours[-1].append(node_index)そして、単純な行 solution.ObjectiveValue() を実行することで目的関数の値にアクセスすることができます。提案された設定を使用して、私は目的関数の値が2679であり、これは証明された最適値である2645に非常に近いです(1.2%のギャップ)。以下に、取得した経路が表示されています。
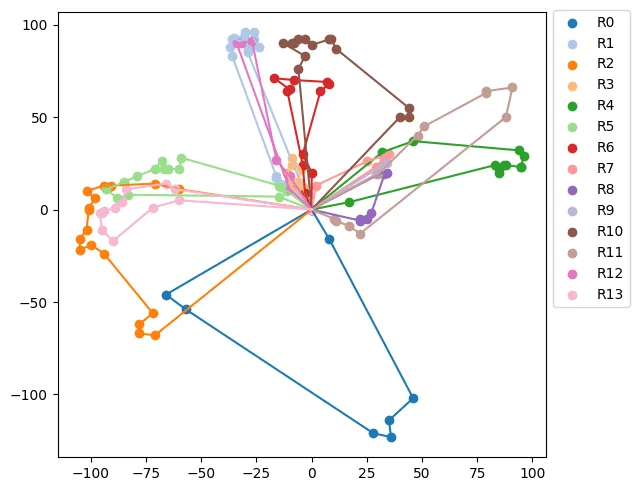
完全なコード(プロットを含む)は、このGitリポジトリで入手できます。
便利な拡張機能
OR Toolsライブラリは、時間枠、異種のフリート、複数のデポなど、VRPのいくつかのバリアントを処理するための一般的なソルバーとして素晴らしいです。ただし、カノニカルCVRPに適したアルゴリズムの方がさらに優れています。最先端の遺伝的アルゴリズムといくつかのローカルサーチ手法を組み合わせたHGS-CVRPパッケージ(Vidal、2022)を確認する価値があります。このアルゴリズムは、インスタンスtai150dの最適解を20秒未満で見つけます。
実世界のアプリケーションに関しては、場所を接続するためにユークリッド距離ではなく道路距離(または所要時間)を使用することが望ましい場合があります。Googleはこれを行うための素晴らしい有料インターフェースを提供しており、これについてはこのチュートリアルをご覧ください。ただし、オープンソースの代替手段をお探しの場合は、OpenStreetMap APIを確認する価値があります。いくつかの便利なリクエストは次のとおりです:
- https://router.project-osrm.org/table/v1/driving/<LOCATIONS>
- http://router.project-osrm.org/route/v1/car/<LOCATIONS>?overview=false&steps=true
<LOCATIONS> は、ペアごとにカンマで区切られ、異なるペア間ではセミコロンで区切られた経度と緯度のリストである必要があります。テーブルリクエストではソースと宛先を指定することもできますが、完全なテーブルが単一のリクエストで処理できない場合に便利です。
正確なルーティング計算を行うだけでなく、可視化は重要なツールになることがあります。Pythonのライブラリfoliumは、それを行うのに非常に便利です。ぜひご覧ください。
さらなる読み物
この記事では、容量制約付き車両ルーティング問題(CVRP)を解決するための2つのアプローチが紹介されました:混合整数プログラミングと(メタ)ヒューリスティクス。最初の代替手法は、小規模なインスタンスを解決するために使用され、成功していますが、中程度から大規模なインスタンスを処理することはできません。2番目のアプローチは、文献からの課題を解決するために使用され、ソルバーは既知の最適解から1.2%のギャップを持つ良質な解を300秒以内に見つけました。
参考文献
Bynum, M. L. et al., 2021. Pyomo-optimization modeling in python. Springer.
Dantzig, G. B., & Ramser, J. H., 1959. The truck dispatching problem. Management science, 6(1), 80–91.
Fukasawa, R., Longo, H., Lysgaard, J., Aragão, M. P. D., Reis, M., Uchoa, E., & Werneck, R. F., 2006. Robust branch-and-cut-and-price for the capacitated vehicle routing problem. Mathematical programming, 106, 491–511.
Pecin, D., Pessoa, A., Poggi, M., & Uchoa, E., 2017. 容量制約付き車両ルーティングのための改良された枝刈りと価格付け。 数理計画計算, 9, 61–100.
Rochat, Y., & Taillard, É. D., 1995. 車両ルーティングのための局所探索における確率的多様化と集中化。 ヒューリスティクス学, 1, 147–167.
Toth, P., & Vigo, D., 2002. 車両ルーティング問題の概要。 車両ルーティング問題, 1–26.
Vidal, T., 2022. CVRPのためのハイブリッド遺伝的探索:オープンソースの実装とSWAP*近傍。 コンピューターとオペレーションリサーチ, 140, 105643.
Vidal, T., Crainic, T. G., Gendreau, M., Lahrichi, N., & Rei, W., 2012. マルチデポと周期的な車両ルーティング問題のためのハイブリッド遺伝的アルゴリズム。 オペレーションリサーチ, 60(3), 611–624.
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
