線形プログラミングを使用して最適化問題を解決する方法
線形プログラミングの最適化問題解決方法
線形計画法の紹介とグラフィカルおよびシンプレックスアルゴリズムを用いた解法について
背景
線形計画法(LP)は、特定の目的関数に対して制約条件を満たす最適解を見つけるために使用される最適化技術です。金融からeコマースまで様々な産業に応用されており、データサイエンティストであるなら知っておく価値があります。LPの特徴は線形であるということで、制約条件と目的関数がすべて線形関係として定式化されます。この投稿では、例題としてLP問題を解く方法としてシンプレックスアルゴリズムとグラフィカルメソッドを紹介します。
グラフィカルメソッド
基本的な問題
まずはじめに、グラフィカルメソッドを使用します。これは理解するのが最も簡単で、LPの背後にある直感を提供してくれます。
例えば、私たちはスムージーを£3で販売し、コーヒーを£2で販売する小規模ビジネスを運営しています。これらは私たちの2つの意思決定変数です。原料の制約により、スムージーは1日に75個、コーヒーは1日に100杯しか作れません。さらに、1日に提供できるカップは140個しかありません。それでは、この問題をLP問題として定式化してみましょう!
定式化
パイをx、コーヒーをyとすると、以下の目的関数cを意思決定変数の関数として最大化したいとします。
以下の制約条件を満たすようになります:
意思決定変数は非負である必要があります。
それでは、これらの制約条件をプロットする時間です!
プロット
この問題は2次元の問題なので、直線(線形の部分!)として制約条件を直交座標グラフにプロットすることができます:
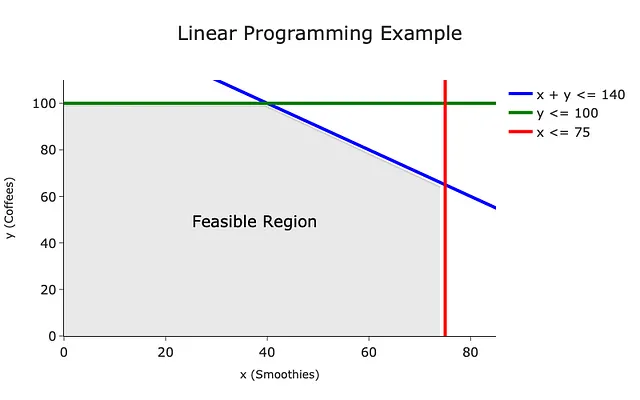
灰色の領域は実行可能領域として知られており、制約条件を満たす任意の解が有効です。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles






