データサイエンティストやアナリストのための統計の基礎
統計の基礎
カール・ピアソンというイギリスの数学者はかつて述べたように、統計学は科学の文法であり、特にコンピュータ情報科学、物理科学、生物科学にとってはそれが当てはまります。データサイエンスやデータ分析の旅を始める際には、統計的な知識を持つことがデータの洞察をより活用するための助けとなります。
「統計学は科学の文法です。」カール・ピアソン
データサイエンスやデータ分析における統計学の重要性は過小評価できません。統計学は構造を見つけ、より深いデータの洞察を与えるためのツールや方法を提供します。統計学と数学の両方は事実を愛し、推測を嫌います。これら2つの重要な科目の基礎を知ることで、ビジネスの問題を解決し、データに基づいた意思決定を行う際に批判的に考え、創造的に活用することができます。本記事では、データサイエンスやデータ分析のための以下の統計学のトピックをカバーします。
- ランダム変数
- 確率分布関数（PDF）
- 平均、分散、標準偏差
- 共分散と相関
- ベイズの定理
- 線形回帰と最小二乗法（OLS）
- ガウス・マルコフの定理
- パラメータの特性（バイアス、一貫性、効率性）
- 信頼区間
- 帰無仮説検定
- 統計的有意性
- 第I種および第II種の誤り
- 統計的検定（スチューデントのt検定、F検定）
- p値とその制約
- 推測統計学
- 中心極限定理と大数の法則
- 次元削減技術（PCA、FA）
もし統計学の事前知識がなく、ゼロから必要な統計学の概念を理解し学ぶこと、そして面接の準備をすることを望んでいる場合は、この記事はあなたにとって役立ちます。また、自身の統計学の知識をリフレッシュしたい方にもおすすめです。
始める前に、LunarTechへようこそ！
LunarTech.aiへようこそ。私たちはデータサイエンスとAIのダイナミックな分野における求職戦略の力を理解しています。競争の激しい求職プロセスをナビゲートするために必要な戦術と戦略に深く入り込んでいます。キャリアの目標を定義すること、応募資料のカスタマイズ、求人掲示板やネットワーキングを活用することなど、私たちの洞察は夢の職に就くために必要なガイダンスを提供します。
データサイエンスの面接の準備をしていますか？心配しないでください！私たちは面接プロセスの複雑さに光を当て、成功の可能性を高めるために必要な知識と準備を提供します。初めの電話スクリーニングから技術的評価、技術面接、行動面接まで、私たちは石をひっくり返しません。
LunarTech.aiでは理論を超えています。私たちはテックとデータサイエンスの世界での圧倒的な成功への飛び込み台です。私たちの包括的な学習の旅は、現代人のライフスタイルにシームレスに組み込むことができ、最新のスキルを身につけながら個人とプロのコミットメントの完璧なバランスを取ることができます。私たちはキャリアの成長に専念し、就職支援、専門的な履歴書作成、面接の準備などを提供します。あなたは業界に即した準備ができたパワーハウスとして浮かび上がるでしょう。
今日、野心的な個人のコミュニティに参加し、このスリリングなデータサイエンスの旅に一緒に乗り出しましょう。LunarTech.aiとともに、未来は明るく、無限の機会を手に入れることができます。
ランダム変数
ランダム変数の概念は多くの統計学の概念の基礎を形成しています。その形式的な数学的な定義を理解するのは難しいかもしれませんが、単純に言えば、ランダム変数はコインを投げるまたはサイコロを振るなどのランダムなプロセスの結果を数値にマッピングする方法です。たとえば、コインを投げるというランダムプロセスをランダム変数Xで定義し、結果が表の場合に値1を取り、結果が裏の場合に値0を取るようにすることができます。
この例では、コインを投げるというランダムプロセスがあり、この実験では2つの可能な結果が生じる可能性があります：{0,1}。このすべての可能な結果の集合を実験の標本空間と呼びます。ランダムプロセスが繰り返されるたびに、それはイベントと呼ばれます。この例では、コインを投げて表が出ることがイベントです。このイベントが特定の結果で発生する確率は、そのイベントの確率と呼ばれます。イベントの確率は、ランダム変数が特定の値xを取る確率を示すP(x)で記述されます。コインを投げる例では、表または裏が出る確率は同じです。つまり、0.5または50%です。したがって、次のような設定があります：
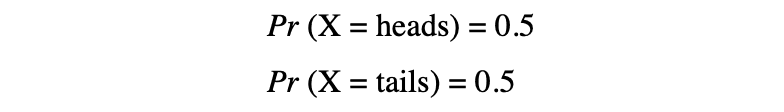
この例では、イベントの確率は値の範囲[0,1]しか取ることができません。
データサイエンスとデータ分析における統計学の重要性は過小評価できません。統計学は構造を見つけ、より深いデータの洞察を得るためのツールと方法を提供します。
平均、分散、標準偏差
平均、分散、およびその他の統計的なトピックを理解するためには、母集団と標本の概念を学ぶことが重要です。母集団はすべての観測値（個人、オブジェクト、イベント、または手順）の集合であり、通常非常に大きく多様です。一方、標本は母集団からの観測値の部分集合であり、理想的には母集団の真の表現です。
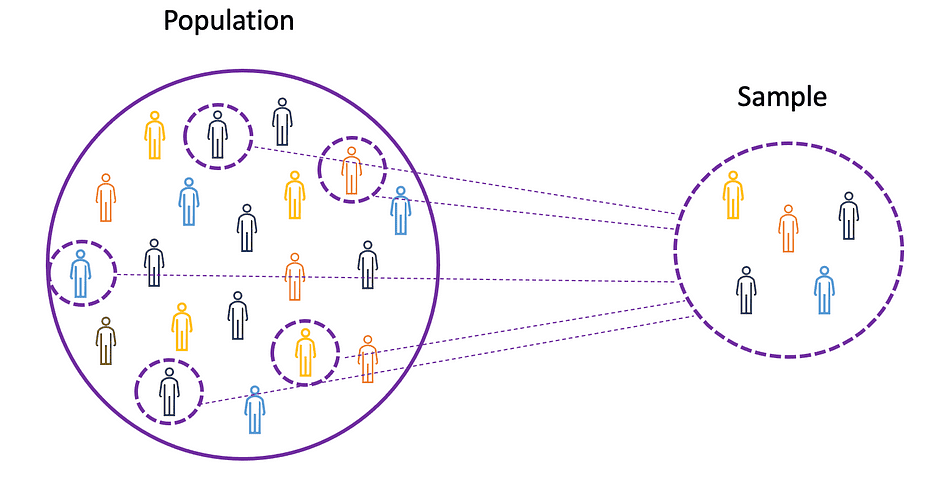
実験対象全体の実験は不可能または単に高すぎるため、研究者やアナリストは実験や試行において母集団全体ではなく標本を使用します。実験結果が信頼性があり、母集団全体に適用されることを確認するためには、標本が母集団の真の表現である必要があります。つまり、標本はバイアスのないものでなければなりません。この目的のために、ランダムサンプリング、系統的サンプリング、クラスターサンプリング、重み付けサンプリング、層別サンプリングなどの統計的サンプリング手法を使用することができます。
平均
平均は有限な数値の集合の中心値であり、平均値としても知られています。データ内のランダム変数Xが次の値を持つと仮定しましょう：
ここで、Nはサンプルセットまたはデータの頻度内の観測値またはデータポイントの数を示します。その場合、サンプル平均は次のように定義され、非常に頻繁に母集団平均を近似するために使用されます：
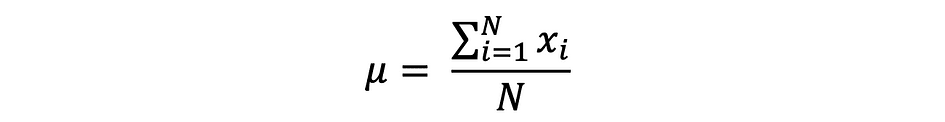
平均は期待値とも呼ばれ、E()または上にバーのあるランダム変数で定義されることもあります。たとえば、ランダム変数XおよびYの期待値、すなわちE(X)およびE(Y)は次のように表されます：
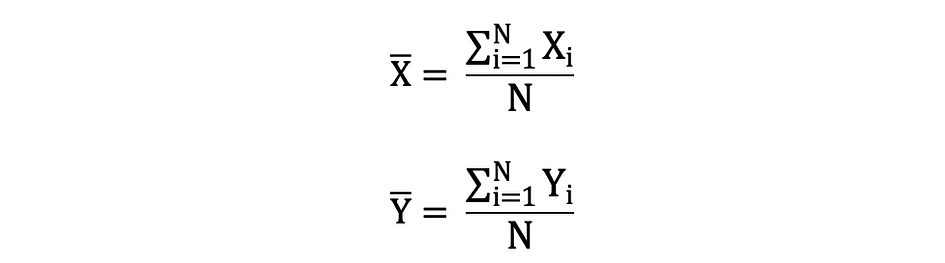
import numpy as np
import math
x = np.array([1,3,5,6])
mean_x = np.mean(x)
# データにNaN値が含まれる場合
x_nan = np.array([1,3,5,6, math.nan])
mean_x_nan = np.nanmean(x_nan)
分散
分散は、データポイントが平均値（平均）からどれだけ広がっているかを測定し、データ値と平均（平均）の差の2乗の合計です。さらに、母集団分散は次のように表されます：
x = np.array([1,3,5,6])
variance_x = np.var(x)
# 自由度（df）を指定する必要がある場合、最大の論理的に独立したデータポイントの数を指定します
x_nan = np.array([1,3,5,6, math.nan])
mean_x_nan = np.nanvar(x_nan, ddof = 1)
異なる人気のある確率分布関数の期待値と分散を導出するためには、このGithubリポジトリをチェックしてください。
標準偏差
標準偏差は、単に分散の平方根であり、データが平均値からどれだけ変動するかを測定します。標準偏差は、以下のように定義されます：
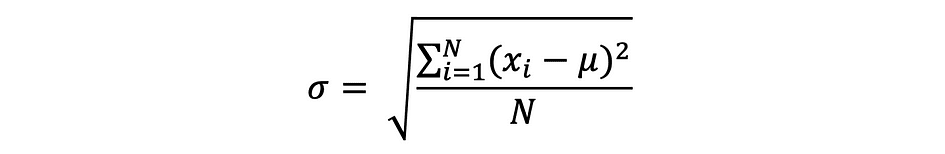
標準偏差は、データポイントと同じ単位を持つため、分散よりも好まれることが多いです。これにより、より簡単に解釈することができます。
x = np.array([1,3,5,6])
variance_x = np.std(x)
x_nan = np.array([1,3,5,6, math.nan])
mean_x_nan = np.nanstd(x_nan, ddof = 1)
共分散
共分散は、2つのランダム変数の共通の変動性を測定し、これら2つの変数間の関係を示します。共分散は、2つのランダム変数の平均からの偏差の積の期待値として定義されます。2つのランダム変数XとZの共分散は、以下の式で表すことができます。ここで、E(X)とE(Z)はそれぞれXとZの平均を表します。
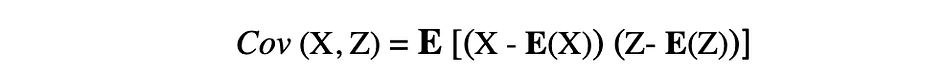
共分散は、負の値、正の値、および値0を取ることがあります。共分散の正の値は、2つのランダム変数が同じ方向に変動する傾向があることを示し、負の値はこれらの変数が逆方向に変動することを示します。最後に、値0はそれらが一緒に変動しないことを意味します。
x = np.array([1,3,5,6])
y = np.array([-2,-4,-5,-6])
# x, yの共分散行列を返します。対角要素にはxの分散、yの分散が含まれ、xとyの共分散が含まれます
cov_xy = np.cov(x,y)
相関
相関は、関係性を測定する指標であり、2つの変数間の線形関係の強さと方向を測定します。相関が検出されると、2つの目標変数の値の間に関係またはパターンがあることを意味します。2つのランダム変数XとZの相関は、以下の式で表される、これら2つの変数の標準偏差の積で共分散を割ったものと等しいです。
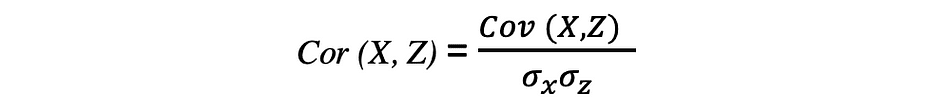
相関係数の値は-1から1の範囲です。自己相関は常に1であることに注意してください、つまりCor(X, X) = 1です。相関を解釈する際には、相関と因果関係を混同しないように注意することも重要です。相関がある場合でも、一つの変数が他の変数に変化を引き起こすとは結論付けることはできません。この関係は偶然の一致である可能性があるだけであり、または第三の要因が両変数の変化を引き起こしているかもしれません。
x = np.array([1,3,5,6])
y = np.array([-2,-4,-5,-6])
corr = np.corrcoef(x,y)
確率分布関数
ある範囲内でランダム変数が取りうるすべての可能な値、つまりサンプル空間と、それに対応する確率を記述する関数を確率分布関数（pdf）または確率密度と呼びます。すべてのpdfは、次の2つの条件を満たす必要があります：
第1の条件は、すべての確率が[0,1]の範囲の数値であることを示し、第2の条件は、すべての可能な確率の合計が1であることを示します。
確率関数は通常、離散と連続の2つのカテゴリに分類されます。離散分布関数は、数えられるサンプル空間でランダムプロセスを記述します。例えば、コインを投げるという場合のように、2つの可能な結果しかない場合です。連続分布関数は、連続的なサンプル空間でランダムプロセスを記述します。離散分布関数の例には、ベルヌーイ、二項、ポアソン、離散一様などがあります。連続分布関数の例には、正規、連続一様、コーシーなどがあります。
二項分布
二項分布は、独立したn回の実験の中で成功の回数の離散確率分布です。各実験は真偽値の結果、つまり成功（確率p）または失敗（確率q = 1 – p）を持ちます。ランダム変数Xが二項分布に従うとすると、n回の独立試行でk回の成功を観測する確率は、以下の確率密度関数で表されます：
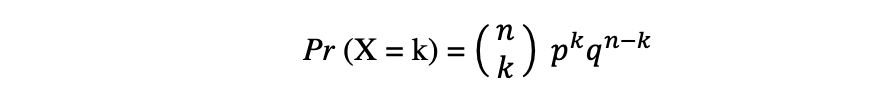
二項分布は、繰り返される独立した実験の結果を分析する際に特に有用です。特定のエラーレートが与えられた場合に特定の閾値に達する確率に興味がある場合に使用されます。
二項分布の平均と分散
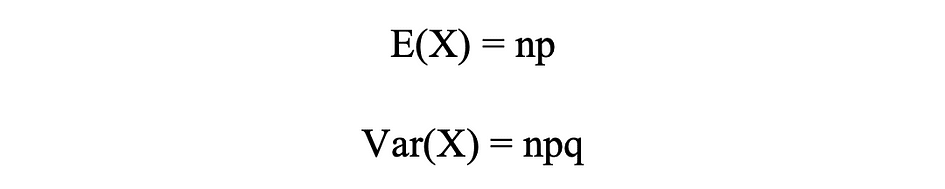
下の図は、独立試行の回数が8回で各試行の成功確率が16％である二項分布の例を可視化しています。
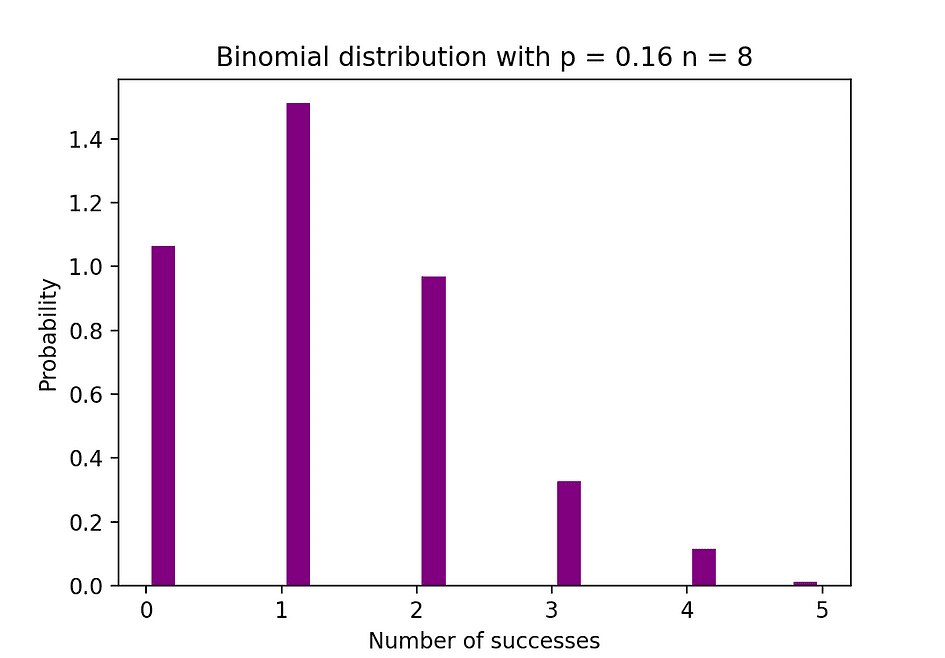Image Source: The Author
# Random Generation of 1000 independent Binomial samples
import numpy as np
n = 8
p = 0.16
N = 1000
X = np.random.binomial(n,p,N)
# Histogram of Binomial distribution
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 20, density = True, rwidth = 0.7, color = 'purple')
plt.title("Binomial distribution with p = 0.16 n = 8")
plt.xlabel("Number of successes")
plt.ylabel("Probability")
plt.show()
ポアソン分布
ポアソン分布は、指定された時間期間内に発生するイベントの数の離散確率分布です。ランダム変数Xがポアソン分布に従うとすると、時間期間内にk個のイベントを観測する確率は、以下の確率関数で表されます：
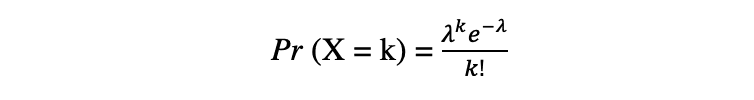
ここで、eはオイラー数、λは到着率パラメータであり、Xの期待値です。ポアソン分布関数は、与えられた時間間隔内で発生するカウント可能なイベントをモデル化するために非常に人気があります。
ポアソン分布の平均と分散
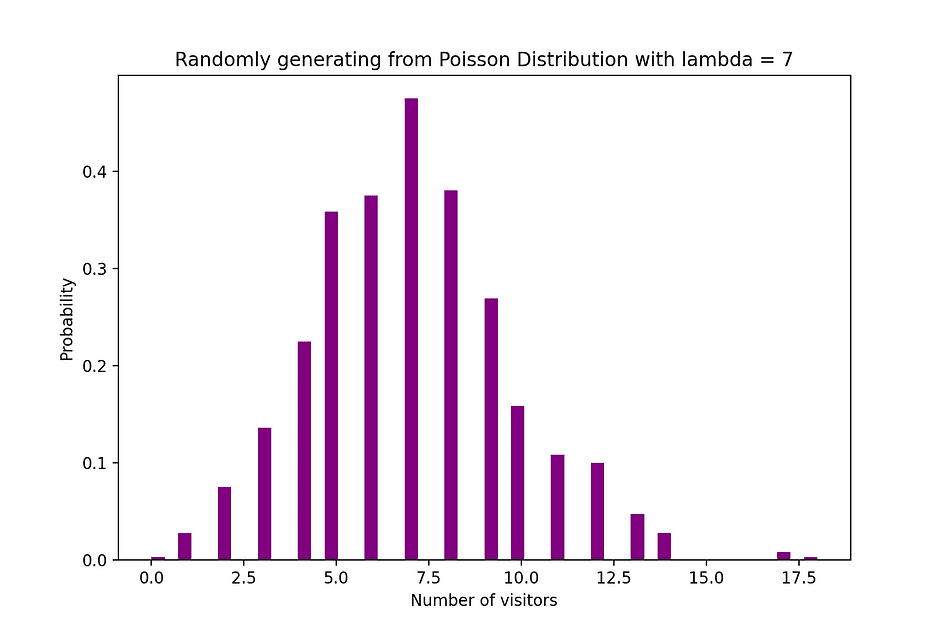
例えば、ポアソン分布は、午後7時から10時までの間に店舗に到着する顧客の数、または午後11時から午前0時までの間に緊急ルームに到着する患者の数をモデル化するために使用することができます。下の図は、到着率λが7分であると仮定したウェブサイトへの訪問者数を数えるポアソン分布の例を可視化しています。
画像の出所: 著者
# 1000個の独立したポアソンサンプルのランダム生成
import numpy as np
lambda_ = 7
N = 1000
X = np.random.poisson(lambda_,N)
# ポアソン分布のヒストグラム
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 50, density = True, color = 'purple')
plt.title("λ=7でポアソン分布からランダムに生成")
plt.xlabel("訪問者数")
plt.ylabel("確率")
plt.show()
正規分布
正規確率分布は、実数値の確率変数のための連続的な確率分布です。正規分布（ガウス分布とも呼ばれる）は、社会科学や自然科学などのモデリングに広く使用される最も一般的な分布関数の一つです。例えば、人々の身長やテストの点数をモデル化するために使用されます。ある確率変数Xが正規分布に従うと仮定すると、その確率密度関数は次のように表されます。
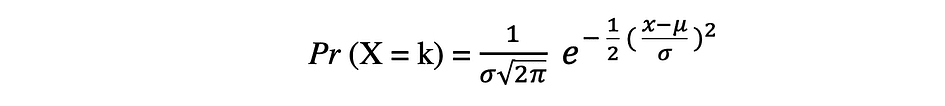
ここで、パラメータ μ（ミュー）は分布の平均であり、位置パラメータとも呼ばれます。パラメータ σ（シグマ）は分布の標準偏差であり、尺度パラメータとも呼ばれます。数値 π（パイ）は、おおよそ3.14と等しい数学定数です。
正規分布の平均と分散
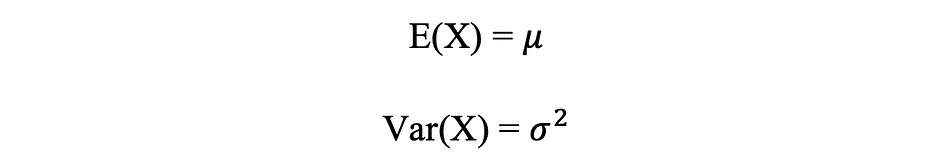
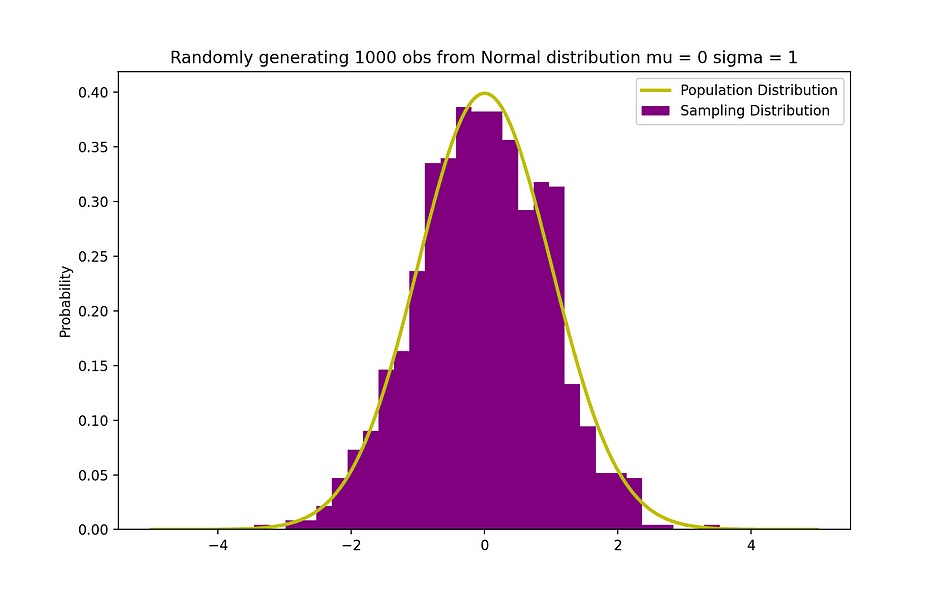
以下の図は、平均が0（μ = 0）で標準偏差が1（σ = 1）の正規分布の例を可視化しています。これは標準正規分布と呼ばれ、対称です。
画像の出所: 著者
# 1000個の独立した正規分布のランダム生成
import numpy as np
mu = 0
sigma = 1
N = 1000
X = np.random.normal(mu,sigma,N)
# 母集団分布
from scipy.stats import norm
x_values = np.arange(-5,5,0.01)
y_values = norm.pdf(x_values)
# 母集団分布とサンプルヒストグラム
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 30, density = True,color = 'purple',label = 'サンプリング分布')
plt.plot(x_values,y_values, color = 'y',linewidth = 2.5,label = '母集団分布')
plt.title("平均0、標準偏差1の正規分布から1000の観測値をランダムに生成")
plt.ylabel("確率")
plt.legend()
plt.show()
ベイズの定理
ベイズの定理、またはよくベイズの法則とも呼ばれるものは、おそらく確率と統計の最も強力な法則であり、有名なイギリスの統計学者兼哲学者、トーマス・ベイズにちなんで名付けられました。
画像の出所: Wikipedia
ベイズの定理は、事実についてのものである統計や数学の世界に主観性の概念をもたらす強力な確率法則です。それは、あるイベントの確率を、そのイベントに関連する条件の事前情報に基づいて記述します。例えば、新型コロナウイルス（COVID-19）にかかるリスクが年齢とともに増加することが知られている場合、ベイズの定理により、特定の年齢の個人のリスクを、その個人が全集団と同様であると単純に仮定するのではなく、年齢に基づいてより正確に決定することができます。
条件付き確率の概念はベイズ理論で中心的な役割を果たし、別の事象が既に発生している場合の事象の発生確率を測定するものです。ベイズの定理は以下の式で表されます。ここで、XとYはそれぞれ事象XとYを表します：
- Pr(X|Y): 条件Yが発生または真である場合に事象Xが発生する確率
- Pr(Y|X): 条件Xが発生または真である場合に事象Yが発生する確率
- Pr(X) & Pr(Y): それぞれ事象XとYが観測される確率
先の例では、ある特定の年齢であること（事象Y）が与えられた場合の新型コロナウイルスの感染確率（事象X）は、新型コロナウイルスの感染確率Pr(X)を特定の年齢である確率Pr(Y|X)で乗じ、特定の年齢である確率Pr(Y)で除したPr(X|Y)と等しくなります。
線形回帰
前述のように、変数間の因果関係は、ある変数が別の変数に直接的な影響を与える場合に発生します。2つの変数の関係が線形である場合、線形回帰は単位変化した変数（独立変数）の値が別の変数（従属変数）の値に与える影響をモデル化するための統計的手法です。
従属変数はしばしば応答変数または説明変数と呼ばれ、独立変数はしばしば回帰変数または説明変数と呼ばれます。線形回帰モデルが単一の独立変数に基づいている場合、そのモデルは単回帰と呼ばれ、複数の独立変数に基づいている場合は重回帰と呼ばれます。単回帰は以下の式で表されます：
ここで、Yは従属変数であり、Xはデータの一部である独立変数、?0は未知の定数である切片、?1は未知の定数であり、変数Xに対応する傾き係数またはパラメータです。最後に、uはモデルがYの値を推定する際に発生する誤差項です。線形回帰の主なアイデアは、一組の（X、Y）のデータに対して最適な適合直線回帰直線を見つけることです。線形回帰の応用例の1つは、ペンギンの体重に対するフリッパーの長さの影響をモデル化することです。
画像の出典: The Author
# グラフのためのRコード
install.packages("ggplot2")
install.packages("palmerpenguins")
library(palmerpenguins)
library(ggplot2)
View(data(penguins))
ggplot(data = penguins, aes(x = flipper_length_mm,y = body_mass_g))+
geom_smooth(method = "lm", se = FALSE, color = 'purple')+
geom_point()+
labs(x="フリッパーの長さ（mm）",y="体重（g）")3つの独立変数を持つ重回帰モデルは以下の式で表されます：
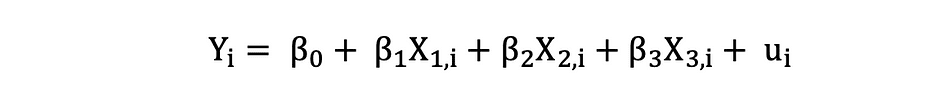
最小二乗法
最小二乗法（OLS）は、線形回帰モデルにおける?0や?1などの未知のパラメータを推定する方法です。このモデルは最小二乗法の原理に基づいており、観測された従属変数と独立変数の線形関数によって予測される値との差の二乗和を最小化します。この差は残差と呼ばれ、OLSは残差の二乗和を最小化することが目標です。この最適化問題の解は、未知のパラメータ?0と?1のOLS推定量としても知られています。
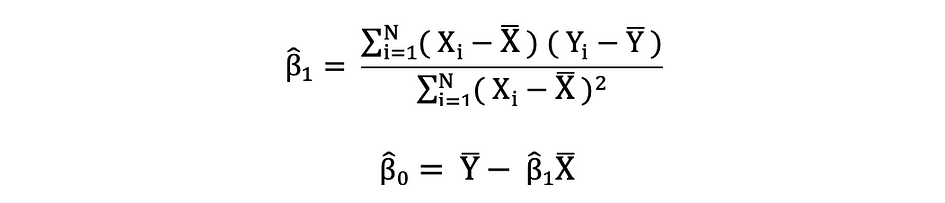
これらの単回帰モデルのパラメータが推定されると、応答変数の適合値は次のように計算できます:
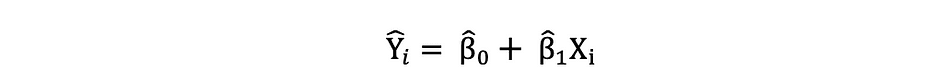
標準誤差
残差または推定された誤差項は次のように決定できます:
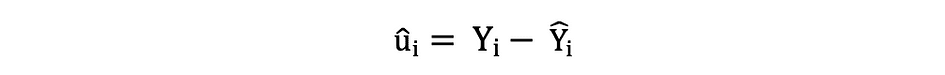
誤差項と残差の違いを念頭に置いておくことは重要です。誤差項は決して観測されませんが、残差はデータから計算されます。OLSは各観測値の誤差項を推定しますが、実際の誤差項ではありません。したがって、真の誤差分散は未知のままです。さらに、これらの推定値は標本抽出の不確実性の影響を受けます。これは、実証的な応用において、標本データからこれらのパラメータの正確な推定値を決定することは決してできないことを意味します。ただし、残差を使用して、以下のように標本残差分散を計算することによってそれを推定することができます。
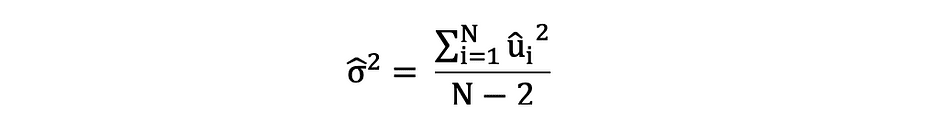
標本残差の分散のこの推定値は、しばしば次のように表される推定パラメータの分散を推定するのに役立ちます:
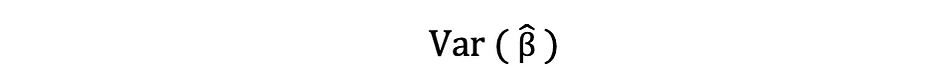
この分散項の平方根を標準誤差と呼び、パラメータ推定の精度を評価するための重要な要素です。これは、テスト統計量と信頼区間の計算に使用されます。標準誤差は次のように表されます:
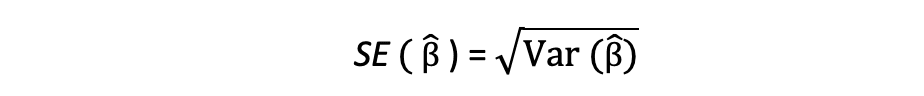
誤差項と残差の違いを念頭に置いておくことは重要です。誤差項は決して観測されませんが、残差はデータから計算されます。
OLSの仮定
OLS推定法は、信頼性のある予測結果を得るために満たされる必要がある次の仮定を行います:
A1: 線形性の仮定は、モデルがパラメータに対して線形であることを述べています。
A2: ランダム サンプルの仮定は、サンプル内のすべての観測値がランダムに選択されていることを述べています。
A3: 外生性の仮定は、独立変数が誤差項と相関していないことを述べています。
A4: ホモスケダスティシティの仮定は、すべての誤差項の分散が一定であることを述べています。
A5: 完全な多重共線性のないことの仮定は、独立変数のいずれも一定ではなく、独立変数間に正確な線形関係がないことを述べています。
def runOLS(Y,X):
# OLS推定 Y = Xb + e --> beta_hat = (X'X)^-1(X'Y)
beta_hat = np.dot(np.linalg.inv(np.dot(np.transpose(X), X)), np.dot(np.transpose(X), Y))
# OLS予測
Y_hat = np.dot(X,beta_hat)
residuals = Y-Y_hat
RSS = np.sum(np.square(residuals))
sigma_squared_hat = RSS/(N-2)
TSS = np.sum(np.square(Y-np.repeat(Y.mean(),len(Y))))
MSE = sigma_squared_hat
RMSE = np.sqrt(MSE)
R_squared = (TSS-RSS)/TSS
# 推定値の標準誤差: 推定値の分散の平方根
var_beta_hat = np.linalg.inv(np.dot(np.transpose(X),X))*sigma_squared_hat
SE = []
t_stats = []
p_values = []
CI_s = []
for i in range(len(beta)):
#標準誤差
SE_i = np.sqrt(var_beta_hat[i,i])
SE.append(np.round(SE_i,3))
#t統計量
t_stat = np.round(beta_hat[i,0]/SE_i,3)
t_stats.append(t_stat)
#t統計量のp値 p[|t_stat| >= t-treshhold two sided]
p_value = t.sf(np.abs(t_stat),N-2) * 2
p_values.append(np.round(p_value,3))
#信頼区間 = beta_hat -+ 誤差の幅
t_critical = t.ppf(q =1-0.05/2, df = N-2)
margin_of_error = t_critical*SE_i
CI = [np.round(beta_hat[i,0]-margin_of_error,3), np.round(beta_hat[i,0]+margin_of_error,3)]
CI_s.append(CI)
return(beta_hat, SE, t_stats, p_values,CI_s,
MSE, RMSE, R_squared)
パラメータの特性
OLSの基準A1〜A5が満たされているという仮定の下で、係数β0とβ1のOLS推定値はBLUEであり一貫性を持っています。
Gauss-Markovの定理
この定理は、OLS推定値の特性を強調しており、BLUEはBest Linear Unbiased Estimatorを表します。
バイアス
推定量のバイアスとは、その期待値と推定されるパラメータの真の値との差であり、以下のように表すことができます：
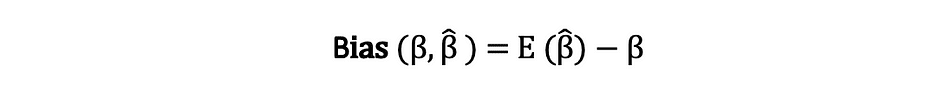
推定量がバイアスがゼロであると述べるとき、それはバイアスがゼロであることを意味し、つまり推定量の期待値が真のパラメータの値と等しいことを意味します：
バイアスがゼロであることは、特定のサンプルで得られた推定値が等しいか、または真の値に近いことを保証するものではありません。それは、集団からランダムにサンプルを何度も抽出し、その都度推定値を計算すると、これらの推定値の平均がβに等しいか非常に近いことを意味します。
効率
Gauss-Markovの定理の中でのBestという用語は、推定量の分散と関連しており、効率と呼ばれます。パラメータには複数の推定量が存在することがありますが、分散が最も小さい推定量が効率的と呼ばれます。
一貫性
一貫性という用語は、標本サイズと収束と密接に関連しています。推定量が真のパラメータに収束するとき、つまり標本サイズが非常に大きくなると、この推定量は一貫性を持つと言われます：
OLSの基準A1〜A5が満たされているという仮定の下で、係数β0とβ1のOLS推定値はBLUEであり一貫性を持っています。 Gauss-Markovの定理
これらの特性は、Gauss-Markovの定理でまとめられるようにOLS推定値に適用されます。言い換えれば、OLS推定値は分散が最も小さく、バイアスがゼロであり、パラメータに対して線形であり、一貫性を持っています。これらの特性は、先に行ったOLSの仮定を使用して数学的に証明することができます。
信頼区間
信頼区間とは、ある一定の事前指定された確率（実験の信頼水準と呼ばれる）で真の母集団パラメータを含む範囲であり、サンプルの結果と誤差の範囲を使用して得られます。
誤差の範囲
誤差の範囲とは、サンプルの結果と、全集団を使用した場合の結果との差です。
信頼水準
信頼水準は、実験結果の確信度を表します。たとえば、95％の信頼水準は、同じ実験を100回繰り返すと、そのうち95回は類似の結果になるという意味です。信頼水準は実験の開始前に定義されるため、実験終了時の誤差の範囲の大きさに影響を与えます。
OLS推定値の信頼区間
前述の通り、単回帰分析のOLS推定値である切片の推定値 ?0 と傾き係数の推定値 ?1 は、サンプリングの不確実性に影響を受けます。しかし、これらのパラメータの真の値を95%の確率で含むCI（信頼区間）を構築することができます。つまり、95%信頼区間は次のように解釈することができます：
- 信頼区間は、仮説検定が5%の水準で棄却されない値の集合です。
- 信頼区間は、真の値 ? を95%の確率で含む可能性があります。
OLS推定値の95%信頼区間は次のように構築することができます：
これは、パラメータの推定値、その推定値の標準誤差、および5%の棄却規則に対応する誤差の範囲を表す値1.96を使用しています。この値は正規分布表を使用して決定されます。詳細については、この記事の後半で説明します。一方、次の図は95%信頼区間のアイデアを示しています：
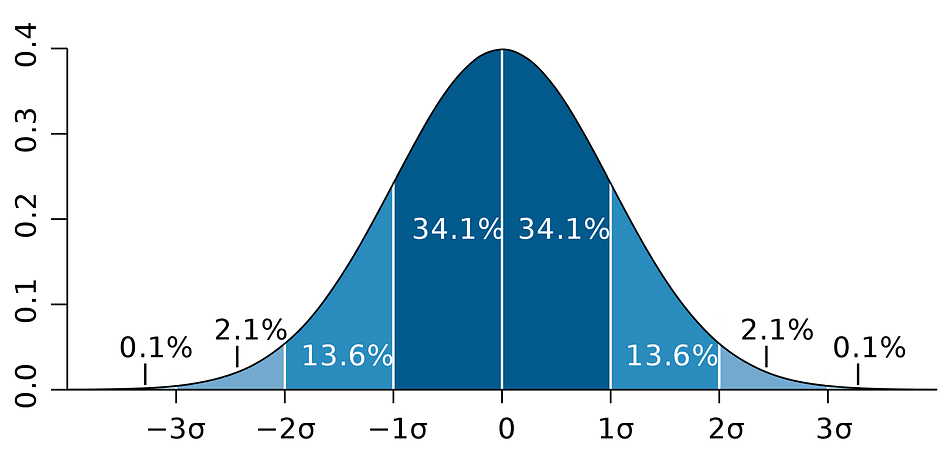画像の出典：Wikipedia
信頼区間は、サンプルサイズにも依存することに注意してください。なぜなら、標準誤差はサンプルサイズに基づいて計算されるからです。
信頼水準は実験の開始前に定義されます。なぜなら、それが実験の終了時の誤差の範囲にどれくらいの影響を与えるかに影響するからです。
統計的仮説検定
統計的仮説検定は、実験や調査の結果をテストして、その結果がどれだけ有意かを判断する方法です。基本的には、結果が偶然に発生した可能性を計算し、その結果が信頼できるかどうかをテストしています。もし結果が信頼できない場合、実験自体も信頼できません。統計的仮説検定は統計的推論の一部です。
帰無仮説と対立仮説
まず、テストしたい仮説を決定し、帰無仮説と対立仮説を定式化する必要があります。テストには2つの可能な結果があり、統計的な結果に基づいて仮説を棄却するか受け入れるかを判断します。統計学者は通常、棄却すべき仮説のバージョンまたは定式化を帰無仮説の下に置き、受け入れることが望ましいバージョンを対立仮説の下に述べる傾向があります。
統計的有意性
先に述べた例を見てみましょう。ここでは、ペンギンのフリッパーの長さ（独立変数）が体重（従属変数）にどのような影響を与えるかを調査するために線形回帰モデルが使用されました。このモデルは次の統計的な式で表すことができます：
その後、係数のOLS推定値が推定されたら、フリッパーの長さが体重に統計的に有意な影響を与えるかどうかをテストするために、次の帰無仮説と対立仮説を定式化することができます：
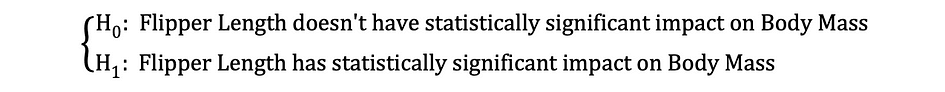
ここで、H0とH1はそれぞれ帰無仮説と対立仮説を表します。帰無仮説を棄却することは、フリッパーの長さが体重に直接的な影響を与えることを意味します。なぜなら、パラメータの推定値 ?1 が独立変数であるフリッパーの長さが従属変数である体重に与えるこの影響を記述しているからです。この仮説は次のように再定式化することができます：
H0は、パラメータ推定値?1が0と等しいことを示しており、つまりFlipper LengthがBody Massに与える影響は統計的に無意味であり、一方、H0はパラメータ推定値?1が0と等しくないことを示しており、Flipper LengthがBody Massに与える影響は統計的に有意であることを示唆しています。
第一種エラーと第二種エラー
統計的仮説検定を行う際には、第一種エラーと第二種エラーの2つの概念的なエラーを考慮する必要があります。第一種エラーは、帰無仮説が誤って棄却される場合に発生し、第二種エラーは、帰無仮説が誤って棄却されない場合に発生します。混乱行列は、これら2つのエラーの深刻さを明確に可視化するのに役立ちます。
統計学者は、通常、帰無仮説のバージョンを棄却する必要があるものとして、帰無仮説の下に述べられた受け入れ可能で望ましいバージョンを代わりに示します。
統計的検定
帰無仮説と対立仮説が述べられ、検定の前提条件が定義されたら、次のステップは適切な統計的検定方法を決定し、検定統計量を計算することです。帰無仮説を棄却するかどうかは、検定統計量を有意水準と比較することで決定することができます。この比較により、観測された検定統計量が定義された有意水準よりも極端であるかどうかが示され、2つの可能な結果が得られます：
- 検定統計量が有意水準よりも極端である場合、帰無仮説は棄却されます
- 検定統計量が有意水準よりも極端ではない場合、帰無仮説は棄却されません
有意水準?（通常は5％とすることが多い）と、検定統計量が従う確率分布のタイプに基づいて、有意水準を超える領域と超えない領域に分割されます。さまざまな仮説を検定するために使用される統計的検定は数多くあります。統計的検定の例には、Studentのt検定、F検定、カイ二乗検定、Durbin-Hausman-Wu内生性検定、Whiteの異分散性検定などがあります。この記事では、これらの統計的検定の2つを見ていきます。
第一種エラーは、帰無仮説が誤って棄却される場合に発生し、第二種エラーは、帰無仮説が誤って棄却されない場合に発生します。
Studentのt検定
最も単純で人気のある統計的検定の1つはStudentのt検定です。これは、単一の変数の統計的に有意な効果の証拠を見つけることが主な関心事である仮説をテストする際に特に使用されます。t検定の検定統計量は、以下のように求めることができます：
ここで、分子のh0は、パラメータ推定値がテストされている値です。つまり、t検定の統計量は、パラメータ推定値から仮説値を引き、係数推定値の標準誤差で割ったものです。先に述べたように、Flipper LengthがBody Massに統計的に有意な影響を与えるかどうかをテストする場合、t検定を使用してこのテストを実行できます。この場合、h0は0と等しいため、傾き係数推定値が値0に対してテストされます。
t検定には2つのバージョンがあります：両側t検定と片側t検定。どちらのバージョンのテストが必要かは、テストしたい仮説に完全に依存します。
両側または両側t検定は、帰無仮説と対立仮説の下での等しい関係と等しくない関係をテストする場合に使用されます。以下の例に似た仮説のテストに適しています：
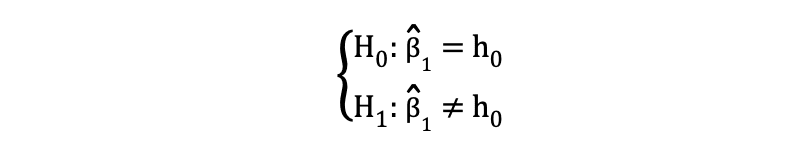
2つの側面t検定は、以下の図に示されるように、2つの拒否領域を持っています：
画像の出典：Hartmann, K., Krois, J., Waske, B. (2018): E-Learning Project SOGA: Statistics and Geospatial Data Analysis. Department of Earth Sciences, Freie Universitaet Berlin
このバージョンのt検定では、計算されたt統計量が小さすぎるか大きすぎる場合にNullが棄却されます。
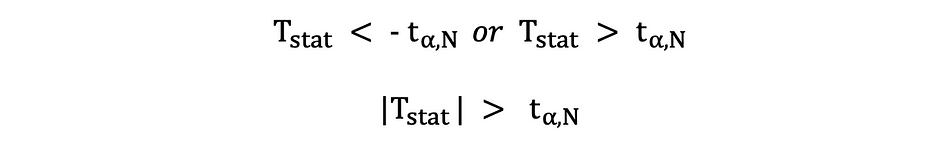
ここでは、検定統計量はサンプルサイズと選択した有意水準に基づいて、臨界値と比較されます。カットオフポイントの正確な値を決定するためには、2つの側面t分布表を使用することができます。
1側または片側t検定は、以下の例に類似するNullと対立仮説の間の正の/負の関係と負の/正の関係をテストする場合に使用できます：
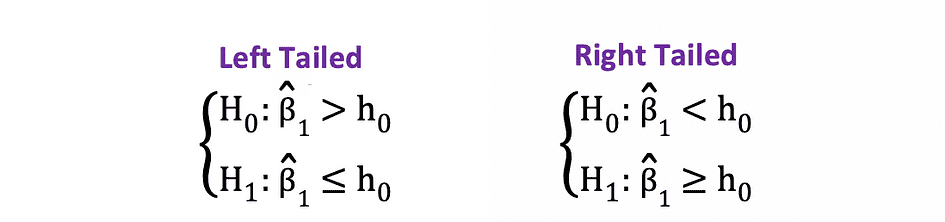
片側t検定には1つの拒否領域があり、仮説の側によって拒否領域は左側または右側になります。
画像の出典：Hartmann, K., Krois, J., Waske, B. (2018): E-Learning Project SOGA: Statistics and Geospatial Data Analysis. Department of Earth Sciences, Freie Universitaet Berlin
このバージョンのt検定では、計算されたt統計量が臨界値より小さい/大きい場合にNullが棄却されます。
F-検定
F-検定は、多くの変数の統計的有意性をテストするために頻繁に使用される別の非常に人気のある統計的検定です。これは、複数の独立変数が従属変数に統計的に有意な影響を与えるかどうかをテストしたい場合に使用されます。次は、F-検定を使用してテストできる統計的仮説の例です：
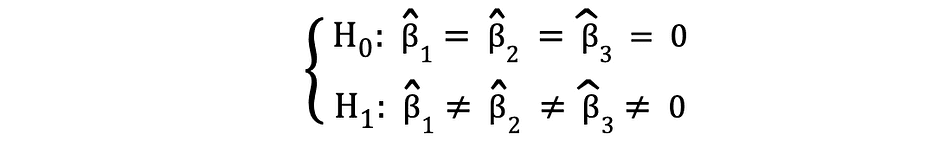
ここで、Nullは、これらの係数に対応する3つの変数が統計的に無意味であるということを述べており、対立仮説は、これらの3つの変数が統計的に有意であると述べています。F-検定の検定統計量はF分布に従い、次のように決定されます：
ここで、SSRrestrictedはNullの下で無意味とされるターゲット変数をデータから除外したモデルである制約モデルの二乗残差の合計です。SSRunrestrictedは、すべての変数を含む非制約モデルの二乗残差の合計です。qはNullの下で無意味として共同テストされる変数の数を表し、Nはサンプルサイズ、kは非制約モデルの変数の総数です。SSRの値はOLS回帰を実行した後のパラメータ推定値の横に表示され、F統計量も同様です。以下は、SSRおよびF統計量の値が表示されているMLRモデルの出力の例です。
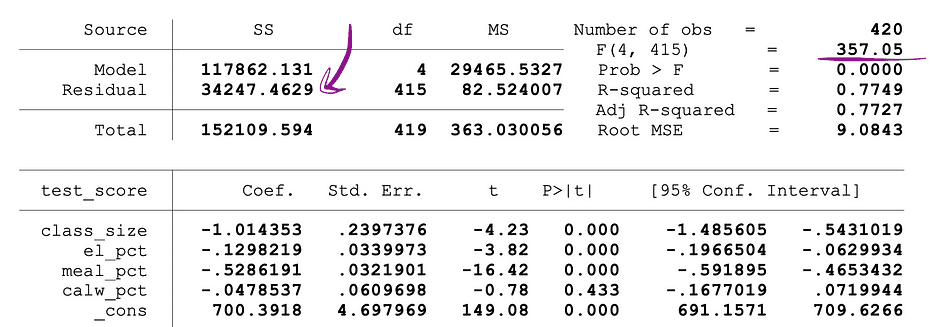画像の出典：Stock and Whatson
F-検定には、以下に示すように1つの拒否領域があります：
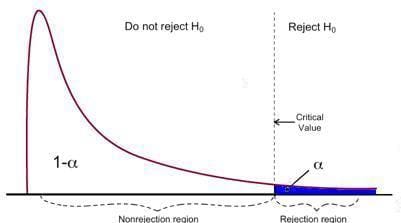画像の出典：U of Michigan
計算されたF統計量が臨界値より大きい場合、帰無仮説は棄却され、独立変数は統計的に有意です。棄却ルールは以下のように表されます：
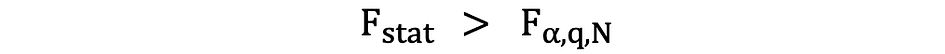
P値
帰無仮説を棄却するか支持するかを判断するもう一つの方法は、p値を使用することです。p値は、帰無仮説の条件が起こる確率です。言い換えると、p値は、帰無仮説が真であると仮定した場合、テスト統計量と同じくらい極端な結果を観測する確率です。p値が小さいほど、帰無仮説に対する証拠が強くなり、棄却できる可能性が高くなります。
p値の解釈は、選択した有意水準に依存します。最もよく使用される有意水準は、1％、5％、または10％です。したがって、t検定とF検定の代わりに、これらの検定統計量のp値を使用して同じ仮説を検定することができます。
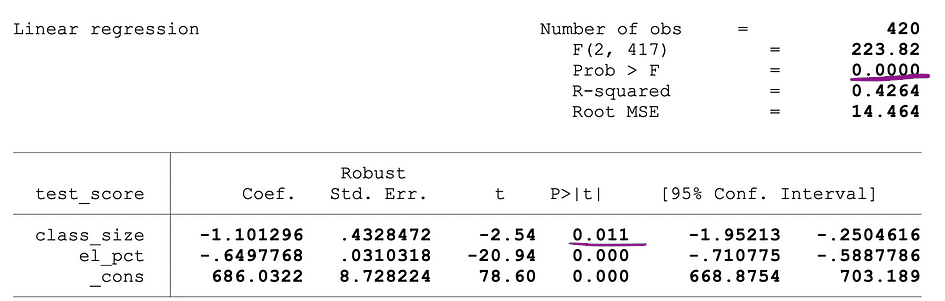
以下の図は、2つの独立変数を持つOLS回帰のサンプル出力を示しています。この表では、class_size変数のパラメータ推定値の統計的有意性を検定するt検定のp値と、class_sizeおよびel_pct変数のパラメータ推定値の統計的有意性を検定するF検定のp値が下線で示されています。
画像の出典：Stock and Whatson
class_size変数に対応するp値は0.011であり、この値を有意水準1％または0.01、5％または0.05、10％または0.1のいずれと比較すると、以下の結論が得られます：
- 0.011 > 0.01 ? t検定の帰無仮説は1％の有意水準で棄却できません
- 0.011 < 0.05 ? t検定の帰無仮説は5％の有意水準で棄却できます
- 0.011 < 0.10 ? t検定の帰無仮説は10％の有意水準で棄却できます
したがって、このp値からは、class_size変数の係数は5％および10％の有意水準で統計的に有意であることが示唆されます。F検定に対応するp値は0.0000であり、0は0.01、0.05、0.10のいずれのカットオフ値よりも小さいため、F検定の帰無仮説はすべての場合で棄却できると結論付けることができます。これは、class_sizeおよびel_pct変数の係数が1％、5％、および10％の有意水準で統計的に有意であることを示唆しています。
p値の制限
p値の使用には多くの利点がありますが、制限もあります。具体的には、p値は関連の大きさとサンプルサイズの両方に依存します。効果の大きさが小さく、統計的に有意でない場合でも、サンプルサイズが大きいため、p値は有意な影響を示す場合があります。逆の場合もあります。効果が大きくても、サンプルサイズが小さい場合は、p＜0.01、0.05、または0.10の基準を満たさない場合があります。
推測統計
推測統計は、サンプルデータを使用してサンプルデータの元となる母集団について合理的な判断をするために使用されます。これは、サンプル内の変数間の関係を調査し、これらの変数がより大きな母集団にどのように関連するかについて予測するために使用されます。
大数の法則（LLN）と中心極限定理（CLM）の両方が推測統計において重要な役割を果たしています。これらは、データが十分に大きい場合、実験結果が元の母集団分布がどのような形であっても成り立つことを示します。データがより多く収集されるほど、統計的推論はより正確になり、したがって、より正確なパラメータ推定値が生成されます。
大数の法則（LLN）
仮定するX1、X2、…、Xnは、すべて同じ基礎分布を持つ独立した確率変数であり、独立同一分布またはi.i.dとも呼ばれます。すべてのXの平均?および標準偏差?も同じです。サンプルサイズが増えるにつれて、すべてのXの平均が平均値?と等しい確率は1に等しくなります。大数の法則は次のように要約できます：
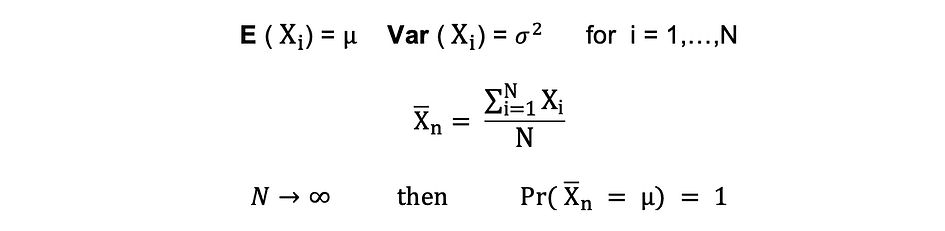
中心極限定理（CLM）
仮定するX1、X2、…、Xnは、すべて同じ基礎分布を持つ独立した確率変数であり、独立同一分布またはi.i.dとも呼ばれます。すべてのXの平均?および標準偏差?も同じです。サンプルサイズが増えるにつれて、Xの確率分布は平均? および分散?-の二乗で正規分布に収束します。中心極限定理は次のように要約できます：
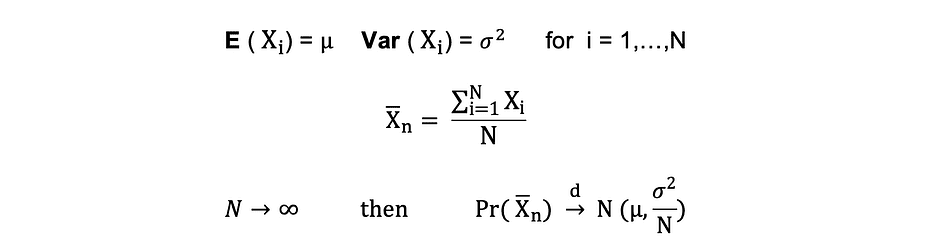
言い換えると、平均値?と標準偏差?を持つ母集団から十分に大きなランダムサンプルを取り、そのサンプルの平均値の分布はほぼ正規分布になります。
次元削減技術
次元削減は、データを高次元空間から低次元空間に変換することで、元のデータの意味のある特性を可能な限り保持したまま、不要なデータと特徴の量を削減することです。
ビッグデータの人気の増加に伴い、これらの次元削減技術の需要も増加しました。よく知られている次元削減技術の例には、主成分分析、因子分析、正準相関、ランダムフォレストなどがあります。
主成分分析（PCA）
主成分分析またはPCAは、大規模なデータセットの次元を削減するために非常に頻繁に使用される次元削減技術です。これにより、多くの情報または元の大規模データセットの変動を保持しながら、多数の変数からなる大規模データセットをより小さなセットに変換することができます。
データXにp個の変数、X1、X2、…..、Xpがあると仮定し、その固有ベクトルe1、…、epと固有値?1、…、?pがあります。固有値は、総分散のうち特定のデータフィールドが説明する分散を示します。PCAのアイデアは、既存の変数の線形結合である新しい（独立した）変数である主成分を作成することです。第i主成分は次のように表されます：
次に、エルボー法またはカイザール法を使用して、データを最適に要約するための主成分の数を決定できます。また、各主成分が説明する総変動の割合（PRTV）を見ることも重要です。これによって、それを含めるか除外するかを決定できます。第i主成分のPRTVは、次のように固有値を使用して計算できます：
エルボー法
エルボー法またはエルボーメソッドは、PCAの結果から最適な主成分の数を決定するために使用されるヒューリスティックな手法です。この方法の背後にある考え方は、説明された変動をコンポーネントの数の関数としてプロットし、曲線の肘（エルボー）を最適な主成分の数として選ぶことです。以下は、PRTV（Y軸）が主成分の数（X軸）にプロットされたそのような散布図の例です。エルボーはX軸の値2に対応し、最適な主成分の数は2であることを示しています。
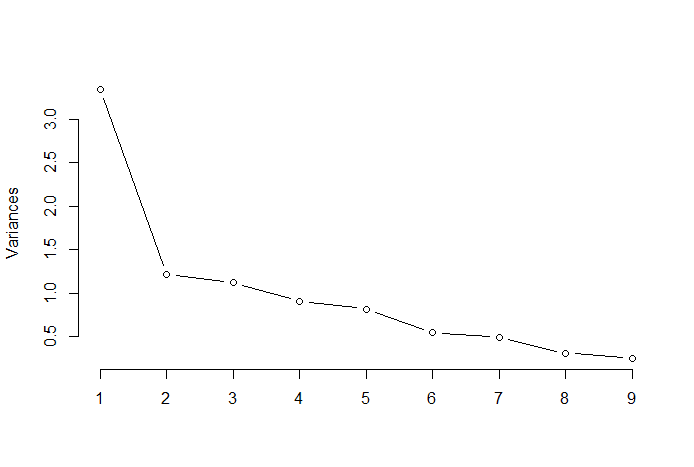画像の出典：Multivariate Statistics Github
因子分析（FA）
因子分析またはFAは、次元削減のための別の統計的手法です。これは最も一般的に使用される相互依存性の技術の一つであり、関連する変数の集合が系統的な相互依存性を示し、共通性を作り出す潜在的な因子を見つけることが目的です。データXがp個の変数（X1、X2、….、Xp）を持つと仮定しましょう。FAモデルは次のように表現されます：
ここで、Xはp個の変数とN個の観測値の[p x N]行列です。µは[p x N]の母集団平均行列、Aは[p x k]の共通因子の荷重行列、F [k x N]は共通因子の行列、u [pxN]は特異因子の行列です。したがって、因子モデルは、各変数Xiを観測されない共通因子fiの値から予測する複数の回帰のシリーズとして表されます：
各変数はそれぞれk個の共通因子を持ち、これらは次のように因子荷重行列を介して観測値に関連しています。因子分析では、因子は群間分散を最大化する一方で群内分散を最小化するように計算されます。これらは変数をグループ化するための因子です。PCAとは異なり、FAではデータを正規化する必要があります。FAはデータセットが正規分布に従うと仮定しています。
Tatev Karen Aslanyan は、機械学習とAIに特化した経験豊富なフルスタックデータサイエンティストです。彼女はオンラインの技術教育プラットフォームであるLunarTechの共同創設者でもあり、The Ultimate Data Science Bootcampの作成者でもあります。Tatev Karenは経済計量学と経営科学の学士号と修士号を持ち、科学的な研究と発表論文に裏打ちされた推薦システムと自然言語処理に焦点を当てた機械学習とAIの分野で成長してきました。5年間の教育の後、Tatevは現在、LunarTechに情熱を傾けており、データサイエンスの未来を形作るのに役立っています。
オリジナル：許可を得て再掲載されました。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
