科学ソフトウェアの開発

科学ソフトウェア開発

パート2：Pythonにおける実践的な側面

この記事では、科学ソフトウェアの開発においてTDDの原則に従い、このシリーズの最初のインストールメントで示されたように、ソーベルフィルタとして知られるエッジ検出フィルタを開発します。

最初の記事では、科学ソフトウェアによく見られる複雑な問題に対して信頼性のあるテスト手法を開発することがどれほど重要であり、また難しいかについて話しました。また、TDDに触発された開発サイクルに従ってこれらの問題を克服する方法も見ましたが、科学計算向けに適応させました。以下にこれらの手順の短縮版を再掲します。

実装サイクル

1. 要件を収集する
2. デザインをスケッチする
3. 初期テストを実装する
4. アルファバージョンを実装する
5. オラクルライブラリを構築する
6. テストを再検討する
7. プロファイリングを実装する

最適化サイクル

1. 最適化する
2. 再実装する

新しいメソッドサイクル

1. 新しいメソッドを実装する
2. 以前のオラクルと検証する

はじめに：ソーベルフィルタ

この記事では、上記の手順に従って、ソーベルフィルタを適用する関数を開発します。ソーベルフィルタは、画像内のエッジを検出または強調するためによく使用されるコンピュータビジョンツールです。いくつかの例をご覧ください。

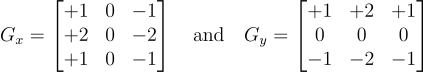
最初のステップから始めましょう。要件をいくつか収集します。この記事で説明されているソーベルフィルタの標準的な形式に従います。単純に言えば、ソーベル演算子は、画像Aを次の2つの3×3のカーネルで畳み込み、結果画像の各ピクセルを二乗し、それらを合算し、点ごとの平方根を取ることで構成されます。AxとAyが畳み込みから得られた画像である場合、ソーベルフィルタSの結果は√(Ax² + Ay²)です。

• 量子コンピューティングは、Q-シリコンの発見によってブーストを受ける可能性があります
• 木材トランジスターが根付く
• バイデン政権、中国へのA.I.チップの販売にさらなる制限検討中

要件

この関数は、任意の2次元配列を受け取り、別の2次元配列を生成するようにしたいです。ndarrayの任意の2つの軸で操作できるようにしたいかもしれません。2つの軸以上（または以下）で動作させることもできるかもしれません。配列のエッジを処理する方法の仕様があるかもしれません。

今のところ、シンプルに保つことを忘れずに、2Dの実装から始めましょう。しかし、その前にデザインをスケッチしましょう。

デザインをスケッチする

Pythonのアノテーションを活用したシンプルなデザインから始めましょう。できるだけ多くの箇所にアノテーションを付けることを強くお勧めし、linterとしてmypyを使用することをお勧めします。

from typing import Tuplefrom numpy.core.multiarray import normalize_axis_indexfrom numpy.typing import NDArraydef sobel(arr: NDArray, axes: Tuple[int, int] = (-2, -1)) -> NDArray:    """画像のソーベルフィルタを計算する    パラメーター    ----------    arr : NDArray        入力画像    axes : Tuple[int, int], オプション        フィルタを計算する軸、デフォルトは(-2, -1)    戻り値    -------    NDArray        出力    """    # 2次元の配列のみ受け付ける    if arr.ndim != 2:        raise NotImplementedError    # axis[0]が最初の軸であり、axis[1]が2番目の軸であることを保証する    # 暗号化された`normalize_axis_index`は負のインデックスを0からarr.ndim - 1までのインデックスに変換します。    if any(        normalize_axis_index(ax, arr.ndim) != i        for i, ax in zip(range(2), axes)    ):        raise NotImplementedError    pass

テストの実装

この関数はあまり多くのことを行いませんが、それはドキュメント化され、注釈が付けられ、現在の制限も組み込まれています。デザインがあるため、すぐにテストに移ります。

まず、空の画像（すべてゼロ）にはエッジがありません。したがって、ゼロを出力する必要があります。実際には、任意の定数画像もゼロを返すべきです。最初のテストにそれを組み込みましょう。また、モンキーテストを使用して多くの配列をテストする方法も見てみましょう。

# test_zero_constant.pyimport numpy as npimport pytest# 同時に複数のデータ型をテスト@pytest.mark.parametrize(    "dtype",    ["float16", "float32", "float64", "float128"],)def test_zero(dtype):    # 乱数のシードを設定    seed = int(np.random.rand() * (2**32 - 1))    np.random.seed(seed)    # ランダムな形状の2次元配列を作成し、ゼロで埋める    nx, ny = np.random.randint(3, 100, size=(2,))    arr = np.zeros((nx, ny), dtype=dtype)    # Sobel関数を適用    arr_sob = sobel(arr)    # `assert_array_equal` はほとんどの場合失敗するはずです。    # 通常、`arr_sob` が完全にゼロである場合にのみ成功します。    # 使用しないでください！    # np.testing.assert_array_equal(    #     arr_sob, 0.0, err_msg=f"{seed=} {nx=}, {ny=}"    # )    # `assert_almost_equal` は高い小数点数で使用すると失敗する可能性があります。    # また、float128の場合にはfloat64のチェックに依存しているため失敗する可能性があります。    # 使用しないでください！    # np.testing.assert_almost_equal(    #     arr_sob,    #     np.zeros_like(arr),    #     err_msg=f"{seed=} {nx=}, {ny=}",    #     decimal=4,    # )    # カスタムの許容範囲を持つ `assert_allclose` がおすすめです    # 10は任意の値であり、問題によって異なります。正しくないメソッドが合格しない場合は、100などに増やしてください。    # テストが合格するために必要な許容範囲が高すぎる場合は、メソッドが実際に正しいことを確認してください。    tol = 10 * np.finfo(arr.dtype).eps    err_msg = f"{seed=} {nx=}, {ny=} {tol=}"  # シードとその他の情報をログに記録    np.testing.assert_allclose(        arr_sob,        np.zeros_like(arr),        err_msg=err_msg,        atol=tol,  # rtolはdesired=zerosでは役に立ちません    )@pytest.mark.parametrize(    "dtype", ["float16", "float32", "float64", "float128"])def test_constant(dtype):    seed = int(np.random.rand() * (2**32 - 1))    np.random.seed(seed)    nx, ny = np.random.randint(3, 100, size=(2,))    constant = np.random.randn(1).item()    arr = np.full((nx, ny), fill_value=constant, dtype=dtype)    arr_sob = sobel(arr)    tol = 10 * np.finfo(arr.dtype).eps    err_msg = f"{seed=} {nx=}, {ny=} {tol=}"    np.testing.assert_allclose(        arr_sob,        np.zeros_like(arr),        err_msg=err_msg,        atol=tol,  # rtolはdesired=zerosでは役に立ちません    )

このコードスニペットは、次のコマンドラインから実行できます。

$ pytest -qq -s -x -vv --durations=0 test_zero_constant.py

アルファバージョン

もちろん、現時点ではテストは失敗するでしょうが、現時点では十分です。最初のバージョンを実装しましょう。

from typing import Tupleimport numpy as npfrom numpy.core.multiarray import normalize_axis_indexfrom numpy.typing import NDArraydef sobel(arr: NDArray, axes: Tuple[int, int] = (-2, -1)) -> NDArray:    if arr.ndim != 2:        raise NotImplementedError    if any(        normalize_axis_index(ax, arr.ndim) != i        for i, ax in zip(range(2), axes)    ):        raise NotImplementedError    # フィルターカーネルを定義します。入力の型を継承していることに注意してください。    # つまり、float32の入力は、計算のためにfloat64にキャストする必要がありません。    # ただし、GxとGyに別のdtypeを使用する場合は、一部の入力dtypeに対して意味があると思いませんか？    Gx = np.array(        [[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]],        dtype=arr.dtype,    )    Gy = np.array(        [[-1, -2, -1], [0, 0, 0], [1, 2, 1]],        dtype=arr.dtype,    )    # 出力配列を作成し、ゼロで埋めます    s = np.zeros_like(arr)    for ix in range(1, arr.shape[0] - 1):        for iy in range(1, arr.shape[1] - 1):            # 要素ごとの積の和、つまり畳み込み            s1 = (Gx * arr[ix - 1 : ix + 2, iy - 1 : iy + 2]).sum()            s2 = (Gy * arr[ix - 1 : ix + 2, iy - 1 : iy + 2]).sum()            s[ix, iy] = np.hypot(s1, s2)  # np.sqrt(s1**2 + s2**2)    return s

この新機能を使用すると、すべてのテストがパスし、次のような出力が得られるはずです：

$ pytest -qq -s -x -vv --durations=0 test_zero_constant.py........======================================== 最も遅い処理時間 =========================================0.09秒 呼び出し     t_049988eae7f94139a7067f142bf2852f.py::test_constant[float16]0.08秒 呼び出し     t_049988eae7f94139a7067f142bf2852f.py::test_zero[float64]0.06秒 呼び出し     t_049988eae7f94139a7067f142bf2852f.py::test_constant[float128]0.04秒 呼び出し     t_049988eae7f94139a7067f142bf2852f.py::test_zero[float128]0.04秒 呼び出し     t_049988eae7f94139a7067f142bf2852f.py::test_constant[float64]0.02秒 呼び出し     t_049988eae7f94139a7067f142bf2852f.py::test_constant[float32]0.01秒 呼び出し     t_049988eae7f94139a7067f142bf2852f.py::test_zero[float16](17 個の処理時間が 0.005 秒未満になっています。これらの処理時間を表示するには -vv を使用します。)8 個のテストが 0.35 秒でパスしました。

現在までに：

1. 問題の要件を収集しました。
2. 初期設計をスケッチしました。
3. いくつかのテストを実装しました。
4. これらのテストに合格するアルファ版を実装しました。

これらのテストは、将来のバージョンに対して検証を提供し、非常に基本的なオラクルライブラリとして機能します。しかし、ユニットテストは期待される結果からの微細な逸脱を捉えるのには優れていますが、誤った結果と定量的に異なるが依然として正しい結果を区別するのには適していません。明日別のSobel型オペレータを実装する場合を考えてみましょう。これにはより長いカーネルがあります。現在のバージョンと完全に一致する結果は期待していませんが、両関数の出力が質的に非常に似ていることを期待しています。

さらに、関数にさまざまな入力を試すことは非常に良い習慣です。これにより、結果を科学的に検証することができます。

Scikit-imageには、オラクルを作成するために使用できる優れた画像ライブラリがあります。

# !pip installscikit-image poochfrom typing import Dict, Callableimport numpy as npimport skimage.databwimages: Dict[str, np.ndarray] = {}for attrname in skimage.data.__all__:    attr = getattr(skimage.data, attrname)    # データは関数呼び出しによって取得されます    if isinstance(attr, Callable):        try:            # データをダウンロードする            data = attr()            # 2次元配列であることを確認する            if isinstance(data, np.ndarray) and data.ndim == 2:                # 精度を評価するために、さまざまなint型をfloat32に変換する                bwimages[attrname] = data.astype(np.float32)        except:            continue# 画像にSobelを適用bwimages_sobel = {k: sobel(v) for k, v in bwimages.items()}

データを取得したら、プロットすることができます。

import matplotlib.pyplot as pltfrom mpl_toolkits.axes_grid1 import make_axes_locatabledef create_colorbar(im, ax):    divider = make_axes_locatable(ax)    cax = divider.append_axes("right", size="5%", pad=0.1)    cb = ax.get_figure().colorbar(im, cax=cax, orientation="vertical")    return cax, cbfor name, data in bwimages.items():    fig, axs = plt.subplots(        1, 2, figsize=(10, 4), sharex=True, sharey=True    )    im = axs[0].imshow(data, aspect="equal", cmap="gray")    create_colorbar(im, axs[0])    axs[0].set(title=name)    im = axs[1].imshow(bwimages_sobel[name], aspect="equal", cmap="gray")    create_colorbar(im, axs[1])    axs[1].set(title=f"{name} sobel")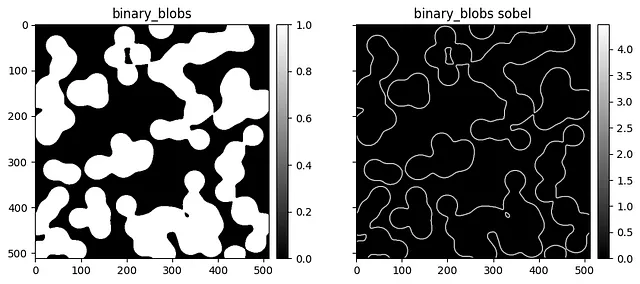

これらはとても良い見た目です！ 新しいバージョンで簡単に確認するために、これらを配列として保存することをおすすめします。配列の保存にはHD5Fを強くお勧めします。また、ドキュメンテーションの更新時に直接図を生成するためにSphinx Galleryを設定することもできます。これにより、以前のバージョンと比較できる再現可能な図のビルドができます。

結果が検証された後、ディスク上に保存してユニットテストの一部として使用できます。以下のような方法です：

oracle_library = [(k, v, bwimages_sobel[k]) for k, v in bwimages.items()]# save_to_disk(oracle_library, ...)

# test_oracle.pyimport numpy as npimport pytestfrom numpy.typing import NDArray# oracle_library = read_from_disk(...)@pytest.mark.parametrize("name,input,output", oracle_library)def test_oracles(name: str, input: NDArray, output: NDArray):    output_new = sobel(input)    tol = 10 * np.finfo(input.dtype).eps    mean_avg_error = np.abs(output_new - output).mean()    np.testing.assert_allclose(        output_new,        output,        err_msg=f"{name=} {tol=} {mean_avg_error=}",        atol=tol,        rtol=tol,    )

プロファイリング

これらのデータセットに対してソベルフィルタを計算するのに時間がかかりました！次のステップは、コードのプロファイリングです。各テストに対してbenchmark_xyz.pyファイルを作成し、定期的に再実行してパフォーマンスの低下を調査することをおすすめします。これはユニットテストの一部にすることもできますが、この例ではそれほど進めません。別のアイデアとして、上記のオラクルをベンチマークに使用することも考えられます。

コードの実行時間を計測する方法は多々あります。システム全体の「実際の」経過時間を取得するには、ビルトインのtimeモジュールのperf_counter_nsを使用してナノ秒単位で時間を計測します。Jupyterノートブックでは、ビルトインの%%timeitセルマジックを使用して特定のセルの実行時間を計測できます。以下のデコレータは、このセルマジックに触発されたもので、任意の関数の実行時間を計測するために使用できます。

import timefrom functools import wrapsfrom typing import Callable, Optionaldef sizeof_fmt(num, suffix="s"):    for unit in ["n", "μ", "m"]:        if abs(num) < 1000:            return f"{num:3.1f} {unit}{suffix}"        num /= 1000    return f"{num:.1f}{suffix}"def timeit(    func_or_number: Optional[Callable] = None,    number: int = 10,) -> Callable:    """実行時間を計測するために関数に適用します。    Parameters    ----------    func_or_number : Optional[Callable], optional        デコレートする関数または`number`引数（以下を参照）、デフォルトはNone    number : int, optional        統計を取得するために関数が実行される回数、デフォルトは10    Returns    -------    Callable        関数が与えられた場合、デコレートされた関数を返します。それ以外の場合はデコレータを返します。    Examples    --------    .. code-block:: python        @timeit        def my_fun():            pass        @timeit(100)        def my_fun():            pass        @timeit(number=3)        def my_fun():            pass    """    if isinstance(func_or_number, Callable):        func = func_or_number        number = number    elif isinstance(func_or_number, int):        func = None        number = func_or_number    else:        func = None        number = number    def decorator(f):        @wraps(f)        def wrapper(*args, **kwargs):            runs_ns = np.empty((number,))            # 最初に実行し、結果を保存            start_time = time.perf_counter_ns()            result = f(*args, **kwargs)            runs_ns[0] = time.perf_counter_ns() - start_time            for i in range(1, number):                start_time = time.perf_counter_ns()                f(*args, **kwargs)  # ストレージなしで高速化                runs_ns[i] = time.perf_counter_ns() - start_time            time_msg = f"{sizeof_fmt(runs_ns.mean())} ± "            time_msg += f"{sizeof_fmt(runs_ns.std())}"            print(                f"{time_msg} per run (mean ± std. dev. of {number} runs)"            )            return result        return wrapper    if func is not None:        return decorator(func)    return decorator

私たちの関数をテストしてみましょう：

arr_test = np.random.randn(500, 500)sobel_timed = timeit(sobel)sobel_timed(arr_test);# 3.9秒± 848.9ミリ秒（10回の平均±標準偏差）

あまり速くありません 🙁

遅さやパフォーマンスの低下を調査する際には、各行の実行時間を追跡することもできます。 line_profiler ライブラリは、このための優れたリソースです。Jupyterセルマジックを介して使用するか、APIを使用することができます。以下にAPIの例を示します：

from line_profiler import LineProfilerlp = LineProfiler()lp_wrapper = lp(sobel)lp_wrapper(arr_test)lp.print_stats(output_unit=1)  # 秒単位の場合は1、ミリ秒単位の場合は1e-3など

以下に出力の例を示します：

Timer unit: 1 sTotal time: 4.27197 sFile: /tmp/ipykernel_521529/1313985340.pyFunction: sobel at line 8Line #      Hits         Time  Per Hit   % Time  Line Contents==============================================================     8                                           def sobel(arr: NDArray, axes: Tuple[int, int] = (-2, -1)) -> NDArray:     9                                               # 2D配列のみ受け入れる    10         1          0.0      0.0      0.0      if arr.ndim != 2:    11                                                   raise NotImplementedError    12                                               13                                               # axis[0]が最初の軸であり、axis[1]が2番目の軸であるようにします    14                                               # あいまいな `normalize_axis_index` は負のインデックスを0からarr.ndim - 1の間のインデックスに変換します    15                                               # インデックス。    16         1          0.0      0.0      0.0      if any(    17                                                   normalize_axis_index(ax, arr.ndim) != i    18         1          0.0      0.0      0.0          for i, ax in zip(range(2), axes)    19                                               ):    20                                                   raise NotImplementedError    21                                               22         1          0.0      0.0      0.0      Gx = np.array(    23         1          0.0      0.0      0.0          [[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]],    24         1          0.0      0.0      0.0          dtype=arr.dtype,    25                                               )    26         1          0.0      0.0      0.0      Gy = np.array(    27         1          0.0      0.0      0.0          [[-1, -2, -1], [0, 0, 0], [1, 2, 1]],    28         1          0.0      0.0      0.0          dtype=arr.dtype,    29                                               )    30         1          0.0      0.0      0.0      s = np.zeros_like(arr)    31       498          0.0      0.0      0.0      for ix in range(1, arr.shape[0] - 1):    32    248004          0.1      0.0      2.2          for iy in range(1, arr.shape[1] - 1):    33    248004          1.8      0.0     41.5              s1 = (Gx * arr[ix - 1 : ix + 2, iy - 1 : iy + 2]).sum()    34    248004          1.7      0.0     39.5              s2 = (Gy * arr[ix - 1 : ix + 2, iy - 1 : iy + 2]).sum()    35    248004          0.7      0.0     16.8              s[ix, iy] = np.hypot(s1, s2)    36         1          0.0      0.0      0.0      return s

内側のループで多くの時間が費やされています。NumPyは、コンパイルされたコードに依存できるため、ベクトル化された数学の使用を好みます。明示的なforループを使用しているため、この関数は非常に遅いと言えます。

さらに、ループ内でのメモリ割り当てについても賢くすることが重要です。 NumPyは、ループ内で小さなメモリを割り当てることに関しては賢いので、s1またはs2を定義している行は新しいメモリを割り当てていないかもしれません。ただし、割り当てが行われる可能性もありますし、私たちが気づいていない裏で発生しているメモリ割り当てがあるかもしれません。そのため、メモリのプロファイリングもおすすめします。私はそれにMemrayを使用するのが好きですが、FilやSciagraphなどの他のツールもあります。また、（非常に残念なことですが！）メンテナンスされていないmemory_profilerも避けることをお勧めします。また、Memrayの方がはるかに強力です。以下はMemrayの実行例です：

$ # プロファイリング情報を保存するsobel.binを作成します$ memray run -fo sobel.bin --trace-python-allocators sobel_run.pyプロファイル結果をsobel.binに書き込んでいますMemray WARNING: aligned_allocのシンボルを0x7fc5c984d8f0から0x7fc5ca4a5ce0に修正しています[memray] プロファイル結果の生成に成功しました。保存された割り当てレコードからレポートを生成できます。レポートを生成するためのいくつかの例：python3 -m memray flamegraph sobel.bin

$ # フレームグラフを生成します$ memray flamegraph -fo sobel_flamegraph.html --temporary-allocations sobel.bin⠙ 高水位を計算しています... ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸  99% 0:00:0100:01⠏ 割り当てレコードを処理しています... ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸  98% 0:00:0100:01sobel_flamegraph.htmlを書き込みました

$ # メモリツリーを表示します$ memray tree --temporary-allocations sobel.bin⠧ 高水位を計算しています... ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 100% 0:00:0100:01⠧ 割り当てレコードを処理しています... ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 100% 0:00:0100:01割り当てのメタデータ-------------------コマンドライン引数: 'memray run -fo sobel.bin --trace-python-allocators sobel_run.py'ピークメモリサイズ: 11.719MB割り当ての数: 15332714最も大きな10の割り当て:-----------------------📂 123.755MB (100.00 %) <ROOT>  └── [[3 frames hidden in 2 file(s)]]    └── 📂 123.755MB (100.00 %) _run_code  /usr/lib/python3.10/runpy.py:86        ├── 📂 122.988MB (99.38 %) <module>  sobel_run.py:40        │   ├── 📄 51.087MB (41.28 %) sobel  sobel_run.py:35        │   ├── [[1 frames hidden in 1 file(s)]]        │   │   └── 📄 18.922MB (15.29 %) _sum          │   │       lib/python3.10/site-packages/numpy/core/_methods.py:49        │   └── [[1 frames hidden in 1 file(s)]]        │       └── 📄 18.921MB (15.29 %) _sum          │           lib/python3.10/site-packages/numpy/core/_methods.py:49...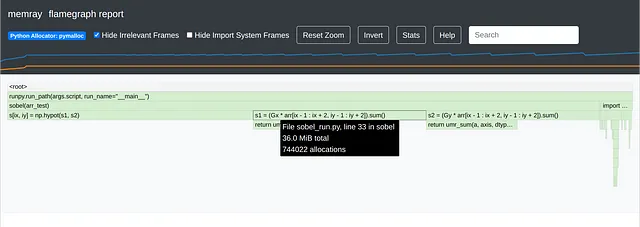

ベータ版とバグ

動作するアルファ版といくつかのプロファイリング関数を持っているので、SciPyライブラリを活用してはるかに高速なバージョンを得ることにします。

from typing import Tupleimport numpy as npfrom numpy.core.multiarray import normalize_axis_indexfrom numpy.typing import NDArrayfrom scipy.signal import convolve2ddef sobel_conv2d(    arr: NDArray, axes: Tuple[int, int] = (-2, -1)) -> NDArray:    if arr.ndim != 2:        raise NotImplementedError    if any(        normalize_axis_index(ax, arr.ndim) != i        for i, ax in zip(range(2), axes)    ):        raise NotImplementedError        # カーネルを単一の複素配列として作成します。 magnitudeを計算するためにnp.absを使用できるようにします。    G = np.array(        [[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]],        dtype=arr.dtype,    )    G = G + 1j * np.array(        [[-1, -2, -1], [0, 0, 0], [1, 2, 1]],        dtype=arr.dtype,    )    s = convolve2d(arr, G, mode="same")    np.absolute(s, out=s)  # In-place abs    return s.real

sobel_timed = timeit(sobel_conv2d)sobel_timed(arr_test)# 14.3 ms ± 1.71 ms per loop (mean ± std. dev. of 10 runs)

はるかに良くなりました！しかし、正しいですか？

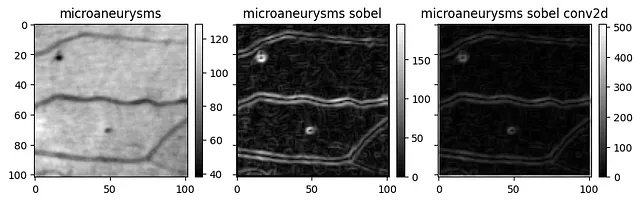
画像は非常に似ていますが、色のスケールを注意してみると、同じではありません。テストを実行すると、わずかな平均誤差が検出されます。幸いにも、私たちは量的および質的な違いを検出するために十分に装備されています。

このバグを調査した結果、異なる境界条件に起因すると考えています。 convolve2d のドキュメントを調べると、カーネルを適用する前に入力配列がゼロでパディングされることがわかります。アルファ版では、出力がパディングされました！

どちらが正しいのでしょうか？おそらく、SciPyの実装の方が理にかなっています。この場合、新しいバージョンをオラクルとして採用し、必要に応じてアルファ版を修正するべきです。これは科学的なソフトウェア開発では一般的です。良い方法で作業するための新しい情報によって、オラクルとテストが変更されます。

この場合、修正は簡単です。配列をゼロでパディングしてから処理を行います。

def sobel_v2(arr: NDArray, axes: Tuple[int, int] = (-2, -1)) -> NDArray:    # ...    arr = np.pad(arr, (1,))  # パディング後の形状は (nx + 2, ny + 2)    s = np.zeros_like(arr)    for ix in range(1, arr.shape[0] - 1):        for iy in range(1, arr.shape[1] - 1):            s1 = (Gx * arr[ix - 1 : ix + 2, iy - 1 : iy + 2]).sum()            s2 = (Gy * arr[ix - 1 : ix + 2, iy - 1 : iy + 2]).sum()            s[ix - 1, iy - 1] = np.hypot(s1, s2)  # インデックスを調整    return s

関数を修正したら、それに依存するオラクルとテストを更新できます。

最後の考え

本記事で探求したソフトウェア開発のアイデアを実践する方法を見ました。高品質で高パフォーマンスなコードを開発するために使用できるツールもいくつか紹介しました。

自分のプロジェクトでこれらのアイデアのいくつかを試してみることをおすすめします。特に、コードのプロファイリングと改善の練習をしてみてください。私たちが作成したソベルフィルタ関数は非常に効率が悪いですので、改善を試してみてください。

たとえば、Numba のようなJITコンパイラを使用してCPU並列化を試したり、内部ループを Cython に移植したり、Numba または CuPy を使用して CUDA GPU 関数を実装したりすることができます。Numba を使用したCUDAカーネルのコーディングに関する私のシリーズもぜひご覧ください。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!