確率的な関係の直感に反する性質

確率的な関係の直感に反する性質' can be condensed as '確率的な関係に反する性質' in Japanese.

yがxの線形関数として推定可能であるということは、xがyの線形関数として推定可能であることを意味しない

実数値の変数xとyを考えます。例えば、父親の身長とその息子の身長です。統計学における回帰分析の中心的な問題は、xを知っている場合にyを推測することです。例えば、父親の身長を基に息子の身長を推測することです¹。

線形回帰のアイデアは、xの線形関数をyの推測として使用することです。形式的には、私たちの推測として ŷ(x) = α₁x + α₀ を考え、yとŷの平均二乗誤差を最小化するために α₀ と α₁ を見つけることです。では、巨大なデータセットを使用して、α₀ と α₁ の最適な値を見つけたとしましょう。つまり、xに基づいてyの最良の推定値を見つける方法を知っています。これらの最適な値を使って、yに基づいてxの推測 x̂(y) を見つけるにはどうすればよいでしょうか？例えば、常に息子の身長に基づいて父親の身長についての最良の推測値を知っている場合、息子の身長に基づいて父親の身長についてどのような推測をするでしょうか？

このような質問は、「どのようにして ŷ(x) を使って x̂(y) を見つけることができるか？」という特殊なケースです。それは簡単に思えるかもしれませんが、この問題は実際には非常に難しいとされています。本稿では、決定論的および確率的な設定での ŷ(x) と x̂(y) の関連について調査し、決定論的な設定では互いにどのように関連しているという私たちの直感が確率的な設定に一般化できないことを示します。

問題の形式的な記述

決定論的設定

決定論的設定とは、(i) 確率的要素がなく、(ii) xの各値が常に同じyの値に対応する状況を指します。形式的には、これらの設定では y = f(x) と書きます。ここで、f: R → R はある関数です。xが完全な確実性でyを決定する場合（つまり、ランダム性やノイズがない場合）、ŷ(x) の最良の選択は f(x) 自体です。例えば、息子の身長が常に父親の身長の1.05倍である場合（今はこの例の不可能性を無視しましょう！）、息子の身長についての最良の推測は、父親の身長に1.05を掛けることです。

• 「OpenAI（Python）APIを解説する」
• 「5層データスタックの構築方法」
• 「人工知能による在庫管理の革命：包括的なガイド」

fが可逆関数である場合、x̂(y) の最良の選択はfの逆関数に等しいです。上記の例では、最良の父親の身長の推測は、常に息子の身長を1.05で割ったものです。したがって、決定論的な場合における ŷ(x) と x̂(y) の関連は直接的であり、関数fとその逆関数を見つけることに帰着できます。

確率的設定

確率的設定では、xとyは確率変数XとYのサンプルです。xの単一の値が複数のyの値に対応する場合、平均二乗誤差を最小化するためのŷ(x) の最良の選択は条件付き期待値 E[Y|X=x] です — 脚注²を参照してください。応用的な言葉で言えば、非常に表現力のあるニューラルネットワークを訓練してxが与えられたときのyを予測する場合、ネットワークはE[Y|X=x] に収束するでしょう。

同様に、x̂(y) の最良の選択は E[X|Y=y] です — yが与えられたときのxを予測するために非常に表現力のあるネットワークを訓練する場合、原則としてE[X|Y=y] に収束します。したがって、確率的設定において ŷ(x) と x̂(y) の関連がどのようになるかという問いは、条件付き期待値 E[Y|X=x] と E[X|Y=y] の関係として再定義することができます。

この記事の目標

この記事では、問題を単純化するために、線形関係に焦点を当てます。つまり、ŷ(x)がxに対して線形である場合を考えます。線形な決定論的関係は、線形な逆関係を持ちます。つまり、y = αx（ただしα≠0）ならば、x = βy（ただしβ = 1/α）となります。詳細は注釈³を参照してください。確率的な線形関係は、決定論的な関係y = αxに対応します。

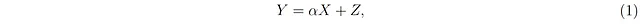
ここで、Zは追加のランダム変数であり、しばしば「ノイズ」または「誤差項」と呼ばれます。条件付き平均はゼロと仮定されており、すべてのxに対してE[Z|X=x] = 0です。なお、ZがXと独立であるとは限りません。式1を使用すると、X=xが与えられた場合のYの条件付き期待値は以下のように表されます（注釈⁴を参照）。

式2は、条件付き期待値ŷ(x)がxに対して線形であることを示しており、それは確率的な線形関係y = αxの確率的な対応物と見なすことができます。

この記事の残りの部分では、次の2つの質問に答えます：

1. 式2がx̂(y) := E[X|Y=y] = βy（ただしβ≠0）を意味するのか？つまり、式2の線形関係には線形な逆関係があるのか？
2. 実際にx̂(y) = βyである場合、決定論的な場合と同様にβ = 1/αと書くことができるのか？

私は2つの反例を使用して、これらの質問の両方に否定的な答えを示します。

例1：βがαの逆ではない場合

最初の例として、線形回帰問題の最も一般的な設定を考えます。以下の3つの仮定に加えて（式1を参照してください）、次のように要約されます（図1Aを参照してください）：

1. 誤差項ZはXと独立です。
2. Xは平均がゼロ、分散が1のガウス分布に従います。
3. Zは平均がゼロ、分散がσ²のガウス分布に従います。

いくつかの代数の計算の後、これらの仮定がYが平均ゼロ、分散α² + σ²のガウス分布に従うことを示すのは簡単です。さらに、これらの仮定から、XとYが平均ゼロ、共分散行列が等しい共同ガウス分布であることも示されます。

XとYの完全な共同分布を持つので、条件付き期待値を導くことができます（脚注⁵を参照）。

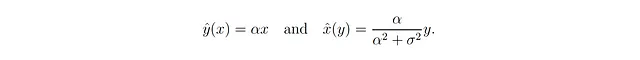
したがって、最初の例の仮定が与えられた場合、方程式2はx̂(y) = βyという形式の線形逆を持つが、βはその決定論的な双子1/αとは異なる場合があります。σ = 0の場合は決定論的な場合相当です！

この結果は、確率的な線形関係についての私たちの直感が決定論的な線形関係に一般化できないことを示しています。この結果が意味する真の狂気をより明確に見るために、まずはα = 0.5で決定論的な設定（σ = 0; 図2Aおよび2Bの青い曲線）を考えてみましょう：

これは、xの値が与えられた場合、yの値がxの半分であり、yの値が与えられた場合、xの値がyの2倍であることを意味し、直感的であるように見えます。重要なことは、常にx < yであることです。次に、α = 0.5でσ² = 3/4（図2Aおよび2Bの赤い曲線）を考えてみましょう。このノイズ分散の選択は、β = α = 0.5を意味し、次のようになります：

これは、xの値が与えられた場合、私たちのyの推定値はxの半分ですが、yの値が与えられた場合、私たちのxの推定値もyの半分です！奇妙なことに、常にx̂(y) < y および ŷ(x) < xであり、これは変数が決定論的である場合は不可能です。反直観的なのは、方程式1を次のように書き直すことができることです：

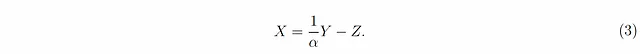
しかし、これは（方程式2とは対照的に）

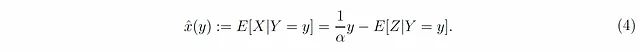
脚注：Z|X=xの条件付き期待値は0であるが、Z|Y=yとそのyに対する依存については何も言えないことに注意してください！つまり、x̂(y)をy/αとは異なるものにするのは、観測値yにも誤差Zについての情報があるためです。たとえば、非常に大きな値のyを観測した場合、それは高い確率で誤差Zも大きな値であることを意味し、Xを推定する際に考慮する必要があります。

<img alt="図2. 例1および例2の線形関係とその逆関係を示す。パネルAは、例1と2（赤色；α = 0.5）の確率的設定におけるŷ(x)とxの線形関係、およびxとyの同等の決定論的関係を示しています（青色）。xに関数としてのŷ(x)が両方の例で同じであることに注意してください。パネルBとCは、例1（Bの赤色；固定σ² = 3/4）および例2（Cの赤色；xに依存するσ²）の確率的設定におけるx̂(y)とyの逆関係を示しています。参照のために、青い線は同等の決定論的関係の逆を示しています。すべてのパネルでは、点線の黒線はy=xの線を示しています。

図2. 例1および例2の線形関係とその逆関係。パネルAは、例1と2（赤色；α = 0.5）の確率的設定におけるŷ(x)とxの線形関係、およびxとyの同等の決定論的関係を示しています（青色）。xに関数としてのŷ(x)が両方の例で同じであることに注意してください。パネルBおよびCは、例1（Bの赤色；固定σ² = 3/4）および例2（Cの赤色；xに依存するσ²）の確率的設定におけるx̂(y)とyの逆関係を示しています。参照のために、青い線は同等の決定論的関係の逆を示しています。すべてのパネルでは、点線の黒線はy=xの線を示しています。

これは、『背の高い父親は平均的に背の高い息子を持つが、自分自身ほど背の高くない』という矛盾した陳述の簡単な説明です。同時に、『背の高い息子は平均的に背の高い父親を持つが、自分自身ほど背の高くない』ということも言えます！

結論として、私たちの例1は、確率的な線形関係ŷ(x) = αxが線形な逆関数x̂(y) = βyを持つ場合でも、傾きβがその決定論的な双子1/αと必ずしも等しくないことを示しています。

例2：x̂(y)が非線形の場合

x̂(y) = βyという形の逆関数を持つことは、式4のE[Z|Y=y]がyの線形関数である場合にのみ可能です。2つ目の例では、この条件を破るために、例1を少し修正します！

具体的には、誤差項Zの分散が確率変数Xに依存すると仮定します（例1の仮定1とは異なります）。形式的には、次のことを仮定します（式1に加えて、図1Bを参照）：

1. Xは平均がゼロで分散が1のガウス分布に従います（例1の仮定2と同じです）。
2. X=xが与えられた場合、誤差Zは平均がゼロで分散がσ² = 0.01 + 1/(1 + 2x²)のガウス分布に従います。

これらの仮定は、X=xが与えられた場合、確率変数Yが平均αx、分散0.01 + 1/(1 + 2x²)のガウス分布に従うことを意味します（図1Bを参照）。例1ではXとYの結合分布がガウス分布であったのに対し、例2ではXとYの結合分布は優雅な形を持ちません（図1Cを参照）。しかし、ベイズの法則を使用して、X=xがY=yの条件下での比較的に複雑な条件付き密度を求めることができます（数値評価の例については図3を参照）：

ここで、曲線Nはガウス分布の確率密度を示します。

<img alt="図3。例2でのY=yの条件付き分布。事前分布p(x)（青の曲線）、尤度p(y|x)（オレンジの曲線）、および事後分布p(x|y)（黒の曲線；式5を使用して数値的に評価）を、左から右にy = 0.5、1.5、2の場合について表示します（すべての場合でα = 0.5を仮定します）。

<img alt="図3。例2でのY=yの条件付き分布。事前分布p(x)（青の曲線）、尤度p(y|x)（オレンジの曲線）、および事後分布p(x|y)（黒の曲線；式5を使用して数値的に評価）を、左から右にy = 0.5、1.5、2の場合について表示します（すべての場合でα = 0.5を仮定します）。

その後、数値的な方法を使用して、与えられたyとαに対して条件付き期待値を評価します。

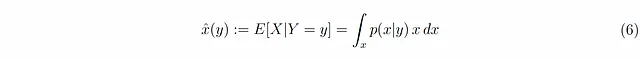
α = 0.5の場合、図2Cはyの関数としてのx̂(y)を示しています。直感に反するかもしれませんが、逆の関係は非常に非線形です。これは、図1Bに示されているxに依存した誤差分散の結果です。つまり、yをxの線形関数としてうまく推定できるという事実は、xをyの線形関数としてうまく推定できるということを意味しません。これは、例1と同様の標準的な仮定を超えたとき、式4のE[Z|Y=y]がyに対してどのような奇妙な関数的依存性を持つかによるものです。

結論として、例2では、確率的な線形関係 ŷ(x) = αx が必ずしも x̂(y) = βy のような線形の逆関係を持つわけではないことが示されています。重要なのは、x̂(y) と y の逆関係は、誤差項 Z の特性に依存するということです。

結論

私たちの教育を通じて、ほとんどの人は決定論的な関係について豊かな直感を築いてきました。微積分や解析などで見たすべての素晴らしい結果に基づいています。しかし、確率的な関係について考える際には、この直感の限界を認識し、信じてはならないということが重要です。特に、例1と例2では、非常に単純な確率的な関係でも、私たちの直感に反する振る舞いをすることが示されています。

謝辞

この記事の内容に関して、Johanni Brea、Mohammad Tinati、Martin Barry、Guillaume Bellec、Flavio Martinelli、Ariane Delrocqによる有益な議論と貴重なフィードバックに感謝しています。

コード:

解析のためのすべてのコード（Julia言語）はこちらで見つけることができます。

脚注:

¹ 興味のある読者は、「父親の身長が息子の身長に与える影響について」をTowards Data Scienceでアクセス可能な形で参照してください。

² 詳細については、Wikipediaの「最小二乗平均誤差」ページを参照してください。

³ 損失のない一般性を失わずに、常にxとyの両方が平均ゼロであると仮定します。したがって、父親と息子の身長の例では、xとyはそれぞれ彼らの身長と父親と息子の平均身長の差を示しています。

⁴ 方程式1と2の関係は逆になります。つまり、方程式2がXとYに対する唯一の制約である場合、常にYをランダム変数Zを用いて方程式1のように書くことができます。ただし、E[Z|X=x] = 0 となるようなランダム変数Zが存在します。

⁵ 詳細は、Wikipediaの「Multivariate normal distribution」ページの「Bivariate conditional expectation」セクションを参照してください。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!