HashGNN Neo4j GDSの新しいノード埋め込みアルゴリズムに深く入り込む
深く入り込むHashGNN Neo4j GDSの新しいノード埋め込みアルゴリズム
この記事では、小さな例を使って、HashGNNがグラフのノードを埋め込み空間にハッシュ化する方法を探求します。
もしビデオで見ることを好む場合は、こちらで視聴することができます。
HashGG(#GNN)は、高次の近接性やノードの特性を捉えるためにメッセージパッシングニューラルネットワーク(MPNN)の概念を採用したノード埋め込み技術です。MinHashingという近似手法を利用することで、従来のニューラルネットワークに比べて計算を大幅に高速化します。したがって、効率と精度のトレードオフを導入するハッシュベースのアプローチです。この記事では、それがどういう意味を持つのかを理解し、アルゴリズムがどのように動作するかを小さな例とともに探求します。
ノードの埋め込み:類似したコンテキストを持つノードは埋め込み空間で近くにあるべきです
リンク予測やノード分類など、多くのグラフ機械学習のユースケースでは、ノードの類似性の計算が必要です。グラフの文脈では、これらの類似性は(i)ノードの近傍(つまりグラフの構造)と(ii)埋め込むノードの特性を捉えるときに最も表現力があります。ノード埋め込みアルゴリズムは、ノードを低次元の埋め込み空間に射影します。つまり、各ノードに数値ベクトルを割り当てます。これらのベクトル(埋め込み)は、さらなる数値予測分析(例:機械学習アルゴリズム)に使用できます。埋め込みアルゴリズムは、次のメトリックに最適化されます:類似したグラフのコンテキスト(近傍)と/または特性を持つノードは、埋め込み空間で近くにマッピングされるべきです。グラフ埋め込みアルゴリズムは通常、次の2つの基本的なステップを使用します:(i)ノードのコンテキストをサンプリングするメカニズムを定義する(node2vecではランダムウォーク、FastRPではk-fold遷移行列)、および(ii)ペアごとの距離を保持しながら次元を削減する(node2vecではSGD、FastRPではランダムプロジェクション)。
HashGNN:ニューラルネットワークのトレーニングを回避する
HashGNNの鍵は、伝統的なメッセージパッシングニューラルネットワークと同様に損失関数に基づいてニューラルネットワークをトレーニングする必要がないということです。ノード埋め込みアルゴリズムは、「埋め込み空間で類似したノードは近くに配置されるべき」という最適化のため、損失の評価にはノードペアの真の類似性の計算が含まれます。これは、予測の正確さと重みの調整にフィードバックとして使用されます。類似性の尺度としては、コサイン類似度がよく使用されます。
HashGNNはモデルのトレーニングを回避し、実際にはニューラルネットワークを全く使用しません。重み行列のトレーニングや損失関数の定義の代わりに、ノードベクトルを同じシグネチャにハッシュ化するランダムハッシング手法を使用します。つまり、ノードを直接比較する必要がない(コサイン類似度を計算する必要がない)でノードを埋め込むことができます。このハッシュ化技術はMinHashingとして知られ、2つの集合の類似性を比較せずに近似するために元々定義されました。集合はバイナリベクトルとしてエンコードされるため、HashGNNはバイナリノード表現を必要とします。一般的なグラフのノードを埋め込むためにこれをどのように使用できるかを理解するには、いくつかの技術が必要です。詳しく見てみましょう。
MinHashing
まず始めに、MinHashingについて話しましょう。MinHashingは、2つの集合のJaccard類似性を近似するための局所的に感知的なハッシング手法です。Jaccard類似性は、2つの集合の重なり(共通部分)を、それらの2つの集合に存在する一意の要素の数(和集合)で割ることによって測定されます。これは、集合に対して定義されるもので、集合はバイナリベクトルとしてエンコードされます:全要素の集合(すべての要素の集まり)には一意の行インデックスが割り当てられます。特定の集合が要素を含む場合、その要素は集合のベクトルの該当する行で値1として表されます。MinHashingアルゴリズムは、各集合のバイナリベクトルを独立にハッシュ化し、Kつのハッシュ関数を使用してK次元のシグネチャを生成します。MinHashingの直感的な説明は、ハッシュ値が最小の非ゼロ要素をK回ランダムに選択することです。これにより、入力集合のシグネチャベクトルが得られます。興味深い部分は、比較せずに2つの集合に対してこれを行うと、Jaccard類似性がある場合には、それらは確率的に同じシグネチャにハッシュされるということです(Kが十分に大きい場合)。言い換えれば、確率はJaccard類似性に収束します。
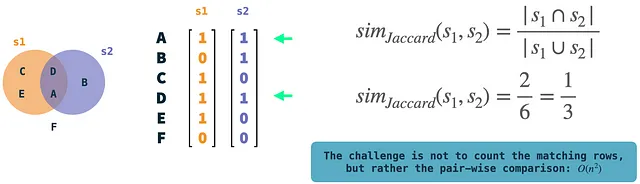
図では、例の集合s1とs2がバイナリベクトルとして表されています。2つを比較し、両方のベクトルが1である行の数を数えることで、Jaccard類似度を簡単に計算できます。これらは非常に単純な操作ですが、多くのベクトルがある場合には、ベクトルのペアごとの比較に複雑さがあります。
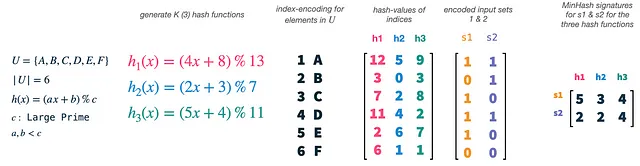
私たちの宇宙Uのサイズは6であり、ハッシュ関数の数Kは3に設定します。単純な式とa、b、cの境界を使用して、新しいハッシュ関数を簡単に生成できます。実際に行うことは、ベクトルのインデックス(1-6)をハッシュ関数のそれぞれでハッシュ化することです。これにより、インデックスとしたユニバースの要素の3つのランダムな順列が得られます。その後、セットベクトルs1とs2を取り、それらを順列された特徴のマスクとして使用します。各順列とセットベクトルについて、セットに存在する最小ハッシュ値のインデックスを選択します。これにより、2つのセットそれぞれに対して3次元ベクトル、つまりセットのMinHashシグネチャが得られます。
MinHashingは単に入力セットからランダムな特徴を選択し、ハッシュ関数はすべての入力セットでこのランダム性を再現する手段としてのみ必要です。すべてのベクトルに対して同じハッシュ関数のセットを使用する必要があるため、2つの入力セットのシグネチャ値は、選択した要素が両方に存在する場合に衝突します。シグネチャ値は、セットのJaccard類似度の確率と衝突します。
WLKNN(Weisfeiler-Lehmanカーネルニューラルネットワーク)
HashGNNは、Weisfeiler-Lehmanカーネルニューラルネットワーク(WLKNN)で定義されたメッセージパッシングスキームを使用して、高階グラフ構造とノードの特性を捉えます。HashGNNのために先述したコンテキストサンプリング戦略を定義します。WLKはT回のイテレーションで実行されます。各イテレーションでは、すべての直接接続された隣接ノードのベクトルとノードの現在のベクトルを組み合わせて、各ノードの新しいノードベクトルを生成します。したがって、隣接ノードに対してメッセージ(ノードベクトル)をエッジに沿って伝達すると考えられます。
T回のイテレーション後、各ノードにはTホップ距離(高階)のノードの情報が含まれています。イテレーションtでの新しいノードベクトルの計算では、隣接メッセージ(イテレーションt-1からのもの)を単一の隣接メッセージに集約し、それを前のイテレーションのノードベクトルと組み合わせます。さらに、WLKNNは3つのニューラルネットワーク(重み行列と活性化関数)を使用します。集約された隣接ベクトル用、ノードベクトル用、および2つを組み合わせたもの用です。イテレーションtでの計算は、イテレーションt-1の結果にのみ依存しているため、マルコフ連鎖と考えることができます。
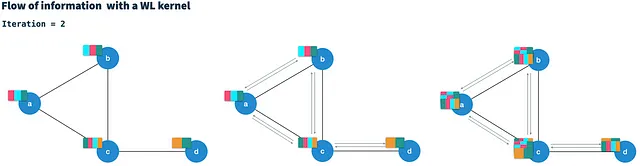
例によるHashGNN
HashGNNが効率的にグラフベクトルを埋め込みベクトルに結合する方法を見てみましょう。WLKNNと同様に、HashGNNアルゴリズムはT回のイテレーションで実行され、前のイテレーションからの隣接ベクトルと自身のノードベクトルを集計して、各ノードに対して新しいノードベクトルを計算します。ただし、3つの重み行列の代わりに、局所感応的ハッシュに対して3つのハッシュスキームを使用します。各ハッシュスキームは、バイナリベクトルからK個のランダムに構築されたハッシュ関数でK個のランダムな特徴を抽出します。
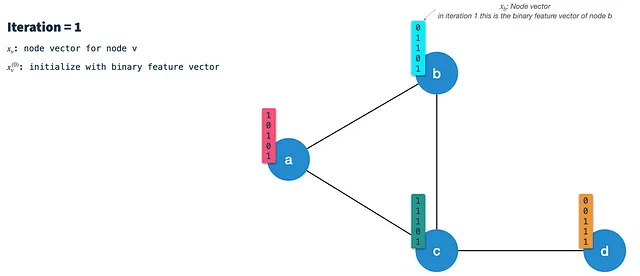
各イテレーションでは、次の手順を実行します:
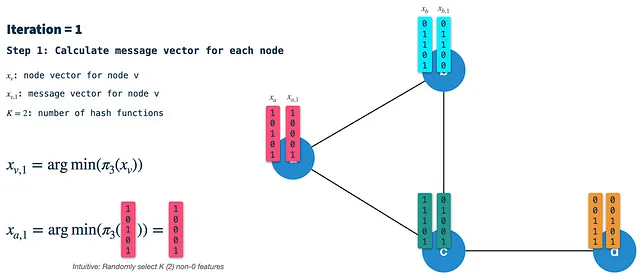
ステップ1:ノードの署名ベクトルを計算する:ハッシュスキーム3を使用して、前のイテレーションのノードベクトルをミニハッシュ(ランダムにK個の特徴を選択)します。最初のイテレーションでは、ノードはバイナリ特徴ベクトルで初期化されます(後でノードをバイナリ化する方法について説明します)。結果として得られる署名(またはメッセージ)ベクトルは、すべての隣接ノードに沿ってエッジに渡されるものです。したがって、すべてのノードについてこれを最初に各イテレーションで行う必要があります。
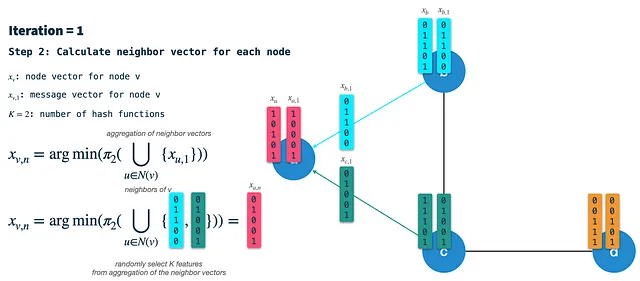
ステップ2:隣接ベクトルを構築する:各ノードでは、直接接続された隣接ノードからの署名ベクトルを受け取り、それらを単一のバイナリベクトルに集約します。その後、ハッシュスキーム2を使用して集約された隣接ベクトルからK個のランダムな特徴を選択し、その結果を隣接ベクトルと呼びます。
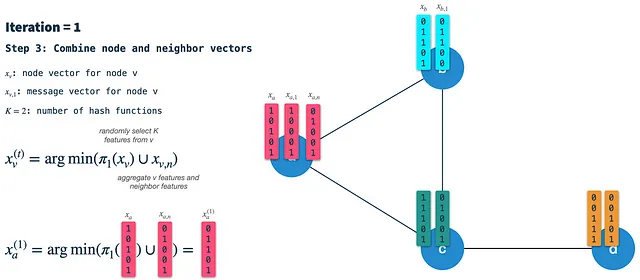
ステップ3:ノードと隣接ベクトルを新しいノードベクトルに結合する:最後に、ハッシュスキーム1を使用して前のイテレーションのノードベクトルからK個のランダムな特徴を選択し、その結果を隣接ベクトルと結合します。その結果得られるベクトルは、次のイテレーションの起点となる新しいノードベクトルです。注意:これはステップ1とは異なります。そこでは、ノードベクトルにハッシュスキーム3を適用してメッセージ/署名ベクトルを構築します。
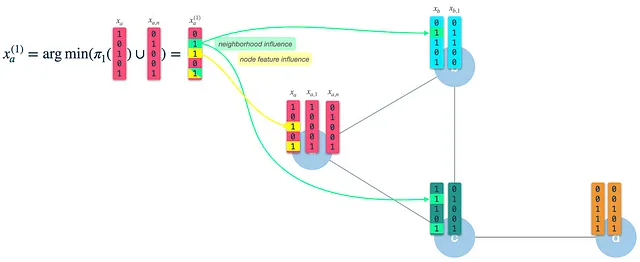
結果として得られる(新しい)ノードベクトルには、自身のノード特徴(3および5)および隣接ノードの特徴(2および5)の影響があることがわかります。イテレーション1の後、ノードベクトルは1ホップ離れた隣接ノードの情報を捉えます。ただし、これをイテレーション2の入力として使用するため、既に2ホップ先の特徴に影響を受けます。
Neo4j GDSの一般化
HashGNNはNeo4j GDS(グラフデータサイエンスライブラリ)によって実装され、アルゴリズムにいくつかの有用な一般化を追加します。
GDSの重要な補助ステップの1つは、特徴のバイナリ化です。MinHashingおよびHashGNNはバイナリベクトルを入力として必要とします。Neo4jは、実数値のノードベクトルをバイナリ特徴ベクトルに変換するための追加の準備ステップを提供しています。彼らはハイパープレーンの丸め処理と呼ばれる技術を利用しています。アルゴリズムは以下のように機能します:
ステップ1:ノードの特徴を定義する: ノードの特徴として使用する(実数値の)ノードプロパティを定義します。これはfeaturePropertiesパラメータを使用して行われます。これをノードの入力ベクトルfと呼びます。
ステップ2:ランダムなバイナリ分類器を構築する: 各ターゲット次元に対して1つのハイパープレーンを定義します。結果の次元数はdimensionsパラメータで制御されます。ハイパープレーンは高次元の平面であり、原点に存在する限り、その法線ベクトルnだけでその向きを表すことができます。 nベクトルは平面の表面に直交しているため、その向きを表します。私たちの場合、nベクトルはノードの入力ベクトルと同じ次元である必要があります(dim(f) = dim(n))。ハイパープレーンを構築するために、単にガウス分布からdim(f)回抽選します。
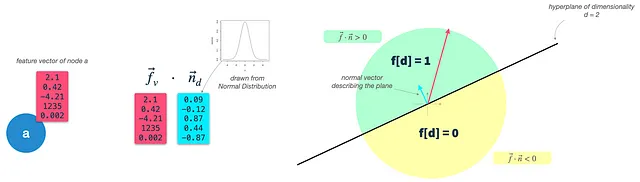
ステップ3:ノードベクトルを分類する: ノードの入力ベクトルと各ハイパープレーンベクトルの内積を計算し、ハイパープレーンと入力ベクトルの間の角度を求めます。 thresholdパラメータを使用して、入力ベクトルがハイパープレーンの上(1)または下(0)にあるかどうかを判断し、結果のバイナリ特徴ベクトルに対応する値を割り当てます。これはバイナリ分類でも行われることですが、ハイパープレーンを反復的に最適化するのではなく、ランダムなガウス分類器を使用します。
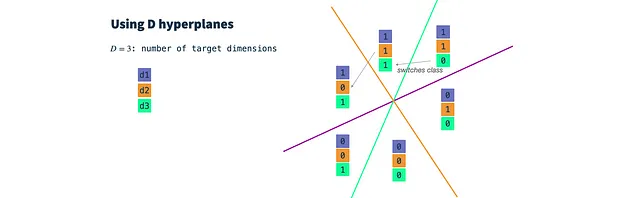
基本的には、各ターゲット次元に対してランダムなガウス分類器を1つずつ抽選し、閾値パラメータを設定します。次に、各ターゲット次元に対して入力ベクトルを分類し、d次元のバイナリベクトルを取得し、HashGNNの入力として使用します。
結論
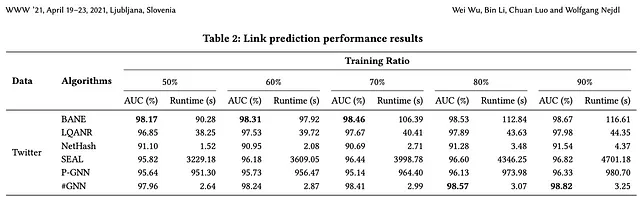
HashGNNは、局所的に感知的なハッシングを使用してノードベクトルを埋め込み空間に埋め込みます。この技術を使用することで、ニューラルネットワークの反復的なトレーニング(または他の最適化)や直接的なノードの比較といった、計算量の多い処理を回避できます。論文の著者は、SEALやP-GNNなどの学習ベースのアルゴリズムと比較して、ランタイムが2〜4桁速く、非常に比較可能な(場合によってはより優れた)精度を生み出すと報告しています。
HashGNNはNeo4j GDS(Graph Data Science Library)で実装されているため、Neo4jグラフ上でそのまま使用することができます。次の投稿では、実際に使用する方法や注意点について詳しく説明します。
ご覧いただきありがとうございました。次回をお楽しみにしてください。🚀
参考文献
- オリジナル論文:リンク予測のためのハッシュアクセラレートされたグラフニューラルネットワーク
- Neo4j GDSドキュメント:HashGNN
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
