時間シリーズのフーリエ変換：画像畳み込みとSciPyについて

時間シリーズのフーリエ変換とSciPyについて

フーリエ変換畳み込みは画像にも適用されます

この投稿は、時系列のためのフーリエ変換の2番目であり、最初の投稿はこちらです：

時系列のためのフーリエ変換：NumPyを使った高速畳み込みの説明

フーリエ変換を使用した10,000倍高速な畳み込み

towardsdatascience.com

前の投稿の簡単なレビュー

最初の投稿では、フーリエ変換を使用して信号を畳み込む方法を非常に効率的に説明しました。NumPyを使用したフーリエ変換による畳み込みが、標準の代数的アプローチよりも桁数以上に高速であり、特定の種類の畳み込みである「循環畳み込み」と対応していることを示しました。

この投稿では、循環畳み込みが意味するものと、それが画像にどのように適用されるかを強調したいと思います。画像も1次元の直感を2次元に拡張する良い方法です。

• GCP ServerlessでTFLiteモデルを展開する
• 「Azureの「Prompt Flow」を使用して、GPTモードで文書コーパスをクエリする」
• 「VAEs、GANs、およびTransformersによる創発的AIの解放」

すべての画像は著者によって作成されました。

scipyを使用した画像畳み込み

画像処理のために画像を扱ったことがある場合、おそらく畳み込みを適用するための関数に遭遇したことがあるでしょう。画像の畳み込みはあらゆる場所で使用されており、画像の強調、ノイズ除去、セグメンテーション、特徴抽出、圧縮に使用され、ビジュアルデータを処理するための深層学習モデルのゴールドスタンダードである畳み込みニューラルネットワークの基礎です。

Pythonでは、画像畳み込みはscipyとそのndimageサブパッケージを使用して非常に簡単に行うことができます。この時点で、`convolve`関数のドキュメントを簡単に確認し、ここに戻ってきてください。

scipy.ndimage.convolve – SciPy v1.11.1 マニュアル

多次元畳み込み。配列は指定されたカーネルと畳み込まれます。パラメータ：入力配列。配列の…

docs.scipy.org

使用方法は非常にシンプルです：2つの画像を渡して一緒に畳み込むことができます。以下に例を示します：

scipyでは、パラメータ「モード」を使用して境界を処理するためのいくつかの方法が提案されています：以下で説明するように、「wrap」モードは循環畳み込みに対応し、したがってフーリエ変換アプローチを使用した畳み込みに対応しています。他のアプローチも存在します。たとえば、画像を内側から外側に反転する「reflect」や、最も外側の値を繰り返す「constant」などです。また、「wrap」がどのように機能するかにも注意してください：周期的であるかのように、信号全体を繰り返します。

2次元画像の畳み込み

異なる畳み込みモードの違いを確認するためにコーディングを始めましょう。

まず、2次元周期的な画像を表すクラスを作成します。前の投稿で説明したように、フーリエ変換ツールを使用する場合、信号は周期的であると見なされます。このクラスは、そのような2次元周期的な配列をプロットするための構文的なシュガーに過ぎません。

「基本」画像を[0、V、0、H]の長方形に表示し、その周りに8つの複製を表示します。前の投稿で述べたように、信号は周期的であるため、無限のサポートを持っていますが、1つの周期のみが必要で使用されます。

次に、遊ぶためのサンプル画像を作成します。それはランダムノイズ、正弦波パターン、勾配パターン、いくつかの四角いスポットを含んでいる必要があります。また、このサンプル画像の周期的なバージョンも作成します。これは、フーリエ変換がその演算子を適用する際に考慮する周期的な画像を表します。

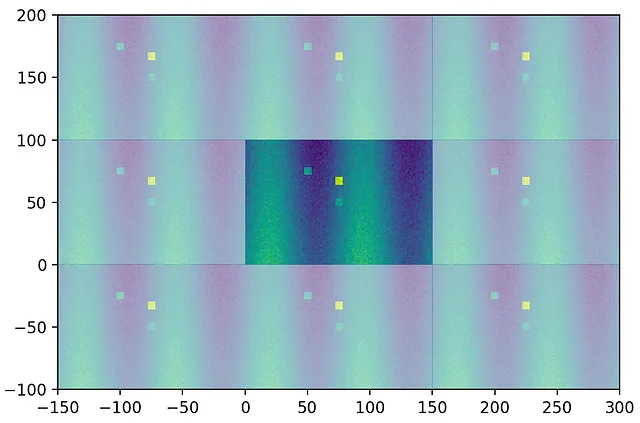
次に、畳み込みに使用するカーネルを作成します。シンプルな定数カーネルを使用します。このカーネルとの畳み込みは、入力画像の局所平均を与えるだけのため、平均化カーネルとも呼ばれます。

次に、scipyの畳み込み関数とその異なるモードで境界を処理し、結果を周期的な配列としてプロットするために遊び始めます：使用されるモードに関係なく、畳み込まれた画像の中央部分は常に同じであることに注意してくださいが、境界は異なります。

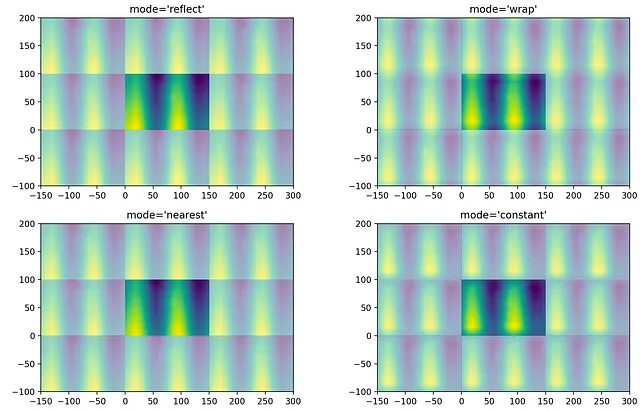
次に、フーリエ変換のアプローチを使用して畳み込みを計算できます：前の投稿で示したように、信号（画像とカーネル）のフーリエ変換の積の逆フーリエ変換を取るだけです：

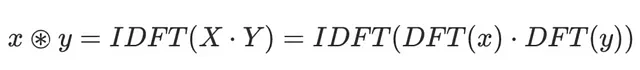
「wrap」モードのscipyと比較すると、結果は非常に似ていることがわかりますが、わずかにシフトしています：

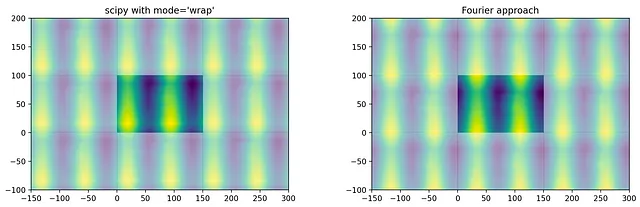
これは単なるインデックスの問題であり、シフトされた中心化されたカーネルを使用して完全に同じ結果を得ることができます：

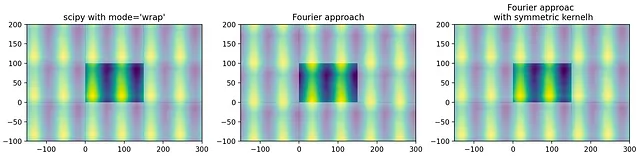
適切な中心化を使用すると、scipyのモード=「wrap」およびフーリエ変換アプローチの間で同じ結果が得られます。

興味本位で、どちらのアプローチの方が速いか見てみましょう：

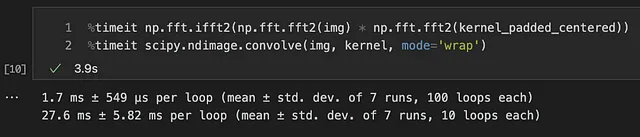
再び、フーリエ変換のアプローチが速く、この場合はscipyの関数よりも速いです。

まとめ

この記事では、円周畳み込みが画像にどのように変換され、scipyの畳み込み関数でのモード=「wrap」の使用と同等であることを見ました。

次の記事では、フーリエ変換の文脈でウィンドウ関数の使用について、スペクトル漏れの削減とスペクトル解析の改善について詳しく説明します。

将来のフーリエ変換に関する投稿をフィードに直接受け取るために購読してください！

また、他の投稿もチェックしてください。気に入ったものがあれば、購読していただけると100人の購読者の目標に到達するのに大いに役立ちます：

時間系列のためのフーリエ変換：numpyを使った高速畳み込みの解説

フーリエ変換を使用した10000倍高速な畳み込み

towardsdatascience.com

PCA/LDA/ICA：コンポーネント解析アルゴリズムの比較

これらの有名なアルゴリズムの概念と違いを復習しましょう。

towardsdatascience.com

PCAホワイトニング対ZCAホワイトニング：numpyによる2Dビジュアル

データのホワイトニングプロセスは、変換されたデータが単位行列を持つような変換です…

towardsdatascience.com

numpyを使用した有限差分法の300倍高速な解像度

有限差分法は複雑な問題を解くための強力な手法であり、numpyはそれを高速化します！

towardsdatascience.com

Jupyterでよく知られたRC回路をインタラクティブにプロットする

ipywidgetsとmatplotlibへのさらなる一歩

towardsdatascience.com

numpyの配列をラップする

コンテナアプローチ。

towardsdatascience.com

これらの記事が興味深いと思われる場合は、フォローしてください。新しい記事はフィードに表示されます。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!