エントロピーを使用した時系列複雑性解析

時系列複雑性解析におけるエントロピー利用

数行のコードで、タイムシリーズの複雑さを理解する方法があります

すべてのデータサイエンティストが知っていることです：機械学習の問題の解決の最初のステップは、データの探索です。

そして、問題を解決するのに役立つ特徴を理解することだけではありません。それは実際にはドメイン知識、多くの努力、多くの質問と調査が必要なものです。それは必要なステップですが、私の意見では、ステップナンバー2です。

最初のステップは、ある意味、形、または形式で、データの複雑さの分析に基づいています。常に同じものですが、微細な詳細やパターンを見つけるよう求められていますか、それとも出力は完全に異なるものですか？ 0.0001と0.0002の間の距離を見つけるよう求められていますか、それとも0と10の間の距離を見つけるよう求められていますか？

私の意図をよりよく説明します。

• 機械学習プロジェクトのロードマップの設計方法
• 「現実的なシミュレーションを用いたデータサイエンスにおけるソフトスキルのトレーニング：ロールプレイデュアルチャットボットアプローチ」
• データサイエンティストになりたいですか？パート1：必要な10つのハードスキル

たとえば、私は信号処理の専門家です。フーリエ変換、チャープレット変換、ウェーブレット変換、ヒルベルト変換、時系列予測、時系列クラスタリング、1D CNN、RNNなど、多くの他の恐ろしい名前を学びました。

時系列ドメインの非常に一般的な問題は、入力（別の時系列かもしれません）から時系列の出力に移ることです。例えば：

• 実験セットアップの特性を持っており、機械学習を使用して実験をシミュレートしたい：これは実際に私の博士論文であり、代替モデルと呼ばれています
• 株式市場の値を300日まで持っており、301日を予測したい：これは非常によく知られており、時系列予測と呼ばれています
• 非常に汚れたまたはノイズの多い信号をクリアしたい：これはエンコーダーデコーダー信号のノイズ除去と呼ばれ、非常によく知られています。

そして、これらの問題では、驚くべきことに、入力ではなく出力の時系列を最初に見ます。

私たちのデータセットからランダムな時系列を取るとしましょう。その時系列は、サインとコサインの優れた組み合わせですか？多項式関数ですか？対数関数ですか？私自身も名前が分からない関数ですか？

そしてもう一つのランダムな時系列を取ると、どのように変わりますか？明らかなベースラインからの小さな変化を見ることに基づくタスクですか、データセット全体で完全に異なる動作を特定するタスクですか？

一言で言えば、私たちはタスクの複雑さを理解しようとしています：私たちは時系列の複雑さを推定しています。ただし、「複雑」という言葉は、それぞれに異なる意味を持つことができます。

妻が解剖学のレッスンを見せてくれたとき、私はそれらを非常に複雑だと感じますが、彼女にとってそれはただの火曜日です ：）

良いニュースは、複雑さをより科学的かつ独自の方法で説明する方法があるということです：エントロピーの概念

1. 1/0時系列のエントロピー（理論）

1と0の値しか持たない時系列からエントロピーを定義しましょう。私たちが通常扱っているタイプの時系列ではないことはわかっていますが、部屋に入るたびにコインを投げると考えることができます：表なら1を測定し、裏なら0を測定したとします（またはその逆、正直に言って1が表であることには特に好みはありません…）

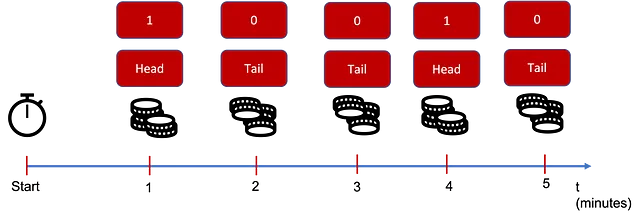
さて、考えてみましょう。何かが「複雑」と感じるのは、それを完全に理解していないときや、大量の情報を提供していないときです。

冗談はやめて、このエントロピーの式を紹介します：

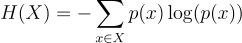
詳しく見ていきましょう：

• Xは時間系列のドメインであり、この場合X = {0,1}です
• p(x)はX内の値xが確率的に出現する確率です

なぜこの中に対数があるのか？それは何を意味しているのか？なぜマイナス符号があるのか？

具体例で学んでみましょう。

Xが0（裏）である確率が0であり、Xが1（表）である確率が1であると想像してください。これは時間系列としてほとんど成り立たないものです。エントロピーの値はいくらになるでしょうか？

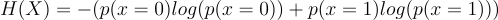
今、p(x=0)=0なので、最初の項は0です。p(x=1)=1ですが、1の対数は0です。したがって、2番目の項も0であり、エントロピーは0です。

エントロピーが0であるとはどういう意味でしょうか？時間系列はまったく複雑ではなく、それは次のように見えます：

この時間系列には「複雑さ」はありませんね。だからエントロピーは0です。

次に、p(x=0)=p(x=1)=0.5で同じ確率で1と0が出現する場合を考えましょう。

これは明らかにより複雑ですね。エントロピーは次のようになります：

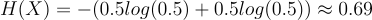
この値自体には意味はありませんが、これは最大の値です。つまり、p(x=0)を0.5と異なる値に変えると、エントロピーは低くなります。

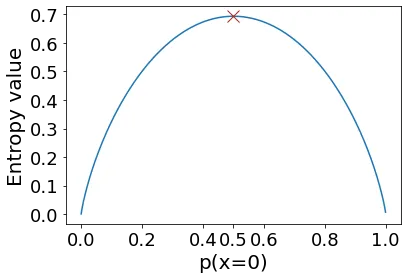
* p(x=0)を変えると同時に、p(x=1)も変化することに注意してください。p(x=1)=1-p(x=0)

これで私たちの発見について考えてみましょう。

• 確率が0の場合、複雑さはないということです。すでにすべてを知っているからです：値は1つだけです。
• 確率が0.0001の場合、複雑さは非常に少ないということです。x=0になることもありますが、大部分の時間ではxは1になる可能性があります。
• 確率が0.5の場合、複雑さが最大になります。次に何が起こるかは全く予測できません：1または0のどちらかが同じ確率で起こる可能性があります。

これは私たちにとっての「複雑さ」の考え方です。単純な1/0の方法で、出現に基づいて確率を逆算し、エントロピーを取得することができます。

2. 1/0時系列のエントロピー（実践）

私たちのコードでは、Pythonを使用し、非常に基本的なライブラリも使用します。

同じ解を見つけるためのコードを書いてみましょうが、確率を「逆算」して、またはお好みで「頻度定義」を使用してみましょう。

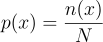
ここで：

• xはドメイン内の値です。この場合、0と1のみなので、xは0または1です
• n(x)は私たちの時系列におけるxの出現回数です
• Nは私たちの時系列の長さです

p(x=0)とp(x=1)を求め、上記の式1を使用します…いいですね、もう一度貼り付けましょう：

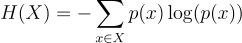
Pythonでは、次の非常に簡単なコードでそれを行うことができます：

それはうまくいきますか？テストしてみましょう！

確率=0.5で長さ100の時系列を生成しましょう：

素晴らしいですね。バランスの取れた時系列ができました。確率を0.5に設定したからといって、ちょうど50と50になるわけではないので、確率の推定にはある種の誤差が生じます。それが私たちが生きている「完璧ではない」世界です 🙂

理論的なエントロピーを計算するための式は次のとおりです：

理論的なエントロピーと実際のエントロピーが一致するか確認してみましょう：

素晴らしい！一致しています！

さて、p_0を変更してみて、引き続き一致するか見てみましょう：

非常にわずかな誤差で一致していますね。そして楽しい部分は、この3回を繰り返すことで私たちの時系列のサイズを増やすと、誤差がますます小さくなることです：

サイズが10kを超えると、実際と予測のエントロピーの間にほとんど差がないことがわかります ❤

3. 任意の時系列のエントロピー

さて、時系列が離散値（0,1,2,…）であると仮定し続ける場合、エントロピーの定義を2つの値だけでなく、はるかに多くの値に拡張することができます。

例えば、三つの値の場合を選んでみましょう。したがって、私たちの時系列は0、1、または2になります。

新しい確率ベクトルp_0、p_1、p_2を作成しましょう。0から100までの3つの乱数を生成し、ベクトルに格納してから、合計で割ります：

前と同じ式（および同じコード）を適用して、実際のエントロピーと予測されるエントロピーを見つけることができます。

エントロピーの定義を拡張しましょう：

これは0/1の場合にも適用できます：

そして、理論的なエントロピーと予測されるエントロピーが三つの値の場合でも一致していることがわかります：

そして、私がうそをついていないことを示すために、p_vector（および時系列）を反復的に変更すると、実際のエントロピーと予測されるエントロピーが一致することを確認できます：

4. 結果

このブログ記事では、以下のことを行いました：

• 機械学習を適用する前に、時系列の複雑さを分析しました
• エントロピーと時系列の無秩序さについて考察しました
• エントロピーの数学的な式を定義し、例を通じて説明しました
• 0/1の時系列と0,1,2の時系列の両方において実践的に適用し、理論的な定義と計算上の近似値が一致することを示しました

現在、このアプローチの問題（制限）は、時系列がこの方法ではうまく機能しない場合があることです。しかし、心配しないでください！ 時系列のための連続エントロピー定義があります。

次のブログ記事で詳しく説明します！

5. 結論

もし記事が気に入ったり、機械学習についてもっと知りたい場合、または何か質問がある場合は、以下の方法で連絡してください：

A. Linkedinで私をフォローしてください。私はすべての記事を投稿しています。

B. 私のニュースレターに登録してください。新しい記事の情報を受け取ることができますし、修正や疑問点があれば連絡することもできます。

C. 推薦メンバーになってください。そのようにすれば、「月の最大記事数」の制限がなくなり、私（および数千人の他の機械学習およびデータサイエンスのトップライター）が提供する最新技術に関する記事を読むことができます。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!