時系列のフーリエ変換:複素数のプロット
時系列のフーリエ変換:複素数のプロット
フーリエ変換アルゴリズムをプロットして理解する
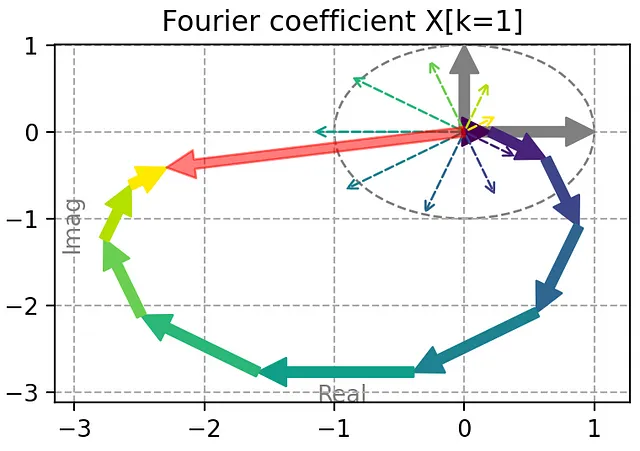
多くの場合、複雑な形式のために信号のフーリエ変換を扱うのに苦労することがあります。非常に特定の場合を除いて、時系列のフーリエ変換はほとんどの場合複素数の数列であり、複素数は常に簡単に理解することができるわけではありません。特にそのような数値を扱うことに慣れていない場合には、さらに理解が難しいです。
この記事では、実数の1次元数列のフーリエ変換を視覚化する方法をいくつか紹介したいと思います。これは、データ分析や時系列の処理など、99%の場合において扱うものです。
すべての画像は筆者によるものです。
この記事は、時系列のフーリエ変換に関する私の3番目の記事です。以前の記事はこちらをご覧ください:
- 畳み込みとフーリエ変換の関係性とその高速性を確認する:
時間系列のフーリエ変換: NumPyを使った高速畳み込みの説明
フーリエ変換を使った10000倍高速な畳み込み
towardsdatascience.com
- 画像の例を使って畳み込みを理解する:
時間系列のフーリエ変換: 画像の畳み込みとSciPyについて
フーリエ変換の畳み込みは画像にも適用されます
towardsdatascience.com
1次元フーリエ変換の実際の計算とプロットに入る前に、次に続く内容に重要な基本的な複素数の概念を再確認します。複素数は実際には非常にシンプルであることがわかります: ただ2つの数値のベクトルとして考えてください。
この記事の最終目標は、フーリエ変換の背後にある実際の数値に対してより快適になることです。
複素数の簡単な復習
任意の複素数は、その標準形を使用して表すことができます。それには2つの実数値、それぞれ「実数」部分と「虚数」部分と呼ばれるaとbがあります:
ここで、iはユニット複素数であり、その二乗がわかっているという特性を持っています…
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles






