ランダムウォークタスクにおける時差0(Temporal-Difference(0))と定数αモンテカルロ法の比較

時差0(Temporal-Difference(0))とαモンテカルロ法の比較

はじめに

モンテカルロ法（MC法）と時系列差分法（TD法）は、強化学習の分野で基本的な技術です。これらの方法は、環境のモデルではなく、環境との相互作用に基づいた経験に基づいて予測問題を解決します。しかし、TD法はMC法と動的計画法（DP）の組み合わせであり、更新規則、ブートストラップ、バイアス/分散の面でMC法とは異なります。TD法は、ほとんどの場合においてMC法と比較して性能が向上し、収束が速いことが証明されています。

この記事では、シンプルなグリッド環境とより包括的なランダムウォーク[2]環境で、TD法とMC法（具体的にはTD(0)と定数αのMC法）を比較します。この記事が、強化学習に興味を持つ読者が、それぞれの方法が状態価値関数をどのように更新し、テスト環境でのパフォーマンスがどのように異なるかをより理解するのに役立てば幸いです。

この記事では、Pythonでアルゴリズムと比較を実装します。以下は、この記事で使用されるライブラリです。

python==3.9.16numpy==1.24.3matplotlib==3.7.1

TD法とMC法の違い

TD(0)と定数αのMC法の紹介

定数αのMC法は、定数のステップサイズパラメータαを持つ通常のMC法であり、この定数パラメータは、値の推定を最近の経験により適切にするのに役立ちます。実際のところ、αの値の選択は、安定性と適応性のトレードオフに依存します。以下は、MC法の時間tでの状態価値関数の更新式です。

• データ、効率化された：より良い製品、ワークフロー、チームの構築方法
• 「データパイプラインにおけるデータ契約の役割」
• 非常に大きなデータセットのランダム化

TD(0)は、一つ先のステップのみを見るTD(λ)の特殊なケースであり、最も単純な形のTD学習です。この方法では、TD誤差（状態の推定値と報酬プラス次の状態の推定値との差）を使用して、状態価値関数を更新します。定数のステップサイズパラメータαは、上記のMC法と同様に機能します。以下は、TD(0)の時間tでの状態価値関数の更新式です。

一般的に言えば、MC法とTD法の違いは以下の3つの側面に現れます：

1. 更新規則：MC法はエピソードの終了後にのみ値を更新します。これは、エピソードが非常に長い場合にプログラムを遅くする問題があります。また、エピソードがまったく存在しない継続タスクの場合も問題となります。対照的に、TD法は各時刻ステップで値の推定を更新します。これはオンライン学習であり、継続タスクでは特に有用です。
2. ブートストラッピング：強化学習における「ブートストラッピング」とは、他の値の推定に基づいて値の推定を更新することを指します。TD(0)法は、次の状態の値に基づいて更新を行うため、ブートストラッピング法です。対照的に、MC法はブートストラッピングを使用せず、値を直接リターン（G）から更新します。
3. バイアス/分散：MC法はバイアスがなく、エピソード中に推定を行わず、実際のリターンを観測した結果を重み付けして値を推定します。しかし、サンプル数が少ない場合、MC法は分散が高くなります。対照的に、TD法はブートストラッピングを使用するため、バイアスがあり、具体的な実装によってバイアスは異なる可能性があります。TD法は、即時の報酬に次の状態の推定値を加えるため、報酬と行動のランダム性から生じる変動を平滑化するため、分散が低くなります。

シンプルなグリッドワールドセットアップでのTD(0)と定数αのMCの評価

その違いを明確にするために、2つの固定軌跡を持つシンプルなGridworldテスト環境を設定し、両アルゴリズムを収束するまで実行し、値の更新方法の違いを確認します。

まず、以下のコードでテスト環境を設定します:

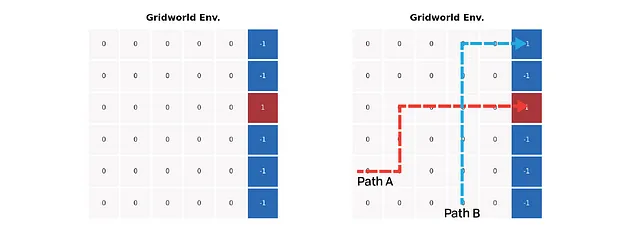
上記の左の図は、シンプルなGridworld環境の設定を示しています。色付きのセルは終端状態を表しており、エージェントは赤いセルに進むと+1の報酬を得ますが、青いセルに進むと-1の報酬を得ます。グリッド上の他のステップでは報酬はゼロです。上記の右の図は、2つの予定経路を示しています。1つは青いセルに到達し、もう1つは赤いセルで停止します。経路の交差点は、2つの方法の値の差を最大化するのに役立ちます。

次に、前のセクションでの方程式を使用して環境を評価します。返却値や推定値を割引せず、αを1e-3という小さな値に設定します。値の増分の絶対値の合計が1e-3以下になると、値が収束したとみなします。

評価の結果は次のようになります:

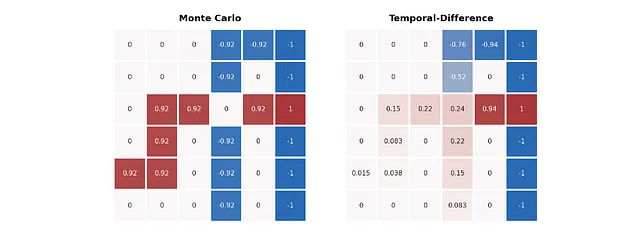
上記の画像では、2つのアルゴリズムの値の推定方法の違いが非常に明確になります。MC法は経路の返り値に忠実であり、各経路の値はそれぞれの終了状態を直接表します。しかし、TD法は特に青い経路でより良い予測を提供します – 交差点の前の青い経路の値も赤いセルに到達する可能性を示しています。

この最小限のケースを念頭に置いて、もっと複雑な例に進み、2つの方法の性能の違いを見つけ出そうとします。

ランダムウォークタスク

ランダムウォークタスクは、TDとMCの予測を目的として提案されたシンプルなマルコフ報酬プロセスであり、以下の画像に示されています。このタスクでは、エージェントは中央のノードCから開始します。エージェントは各ノードで右または左に等しい確率でステップを取ります。チェーンの両端には2つの終端状態があります。左端に到達すると報酬は0で、右端に到達すると+1です。終了までのすべてのステップは報酬0を生成します。

以下のコードを使用してランダムウォーク環境を作成できます:

=====テスト: 環境設定のチェック=====リンク:        None ← ノードA → ノードB報酬:          0 ← ノードA → 0リンク:      ノードA ← ノードB → ノードC報酬:          0 ← ノードB → 0リンク:      ノードB ← ノードC → ノードD報酬:          0 ← ノードC → 0リンク:      ノードC ← ノードD → ノードEReward:          0 ← ノードD → 0リンク:      ノードD ← ノードE → None報酬:          0 ← ノードE → 1

ランダムポリシーの下で環境の各ノードの真の値は[1/6, 2/6, 3/6, 4/6, 5/6]です。この値はベラムの方程式によるポリシー評価で計算されました:

私たちの課題は、両方のアルゴリズムによって推定された値が真の値にどれだけ近いかを見つけることです。真の値関数に対してアルゴリズムがより近い値関数を生成すると仮定し、平均二乗平方根誤差（RMS）によって測定される、より優れたパフォーマンスを示すとします。

TD(0)と定数-a MCのランダムウォーク上のパフォーマンス

アルゴリズム

環境の準備ができたら、ランダムウォーク環境で両方のメソッドを実行し、パフォーマンスを比較します。まず、両方のアルゴリズムを見てみましょう：

前述したように、MC法ではエピソードが終了するまで、軌跡の末尾から値を更新する必要がありますが、TD法では値を段階的に更新します。この違いにより、状態価値関数の初期化にはトリックがあります。MCでは、状態価値関数には終端状態は含まれませんが、TD(0)では、TD(0)法は常にエピソードが終了する前に1ステップ先を見るため、終端状態を値0で含める必要があります。

実装

この実装でのαパラメータの選択は、[2]で提案されたものを参考にしています。MC法のパラメータは[0.01、0.02、0.03、0.04]であり、TD法のパラメータは[0.05、0.10、0.15]です。TDのパラメータがMC法に対して高すぎるため、MCの最適なパフォーマンスが明らかになりませんでした。したがって、パラメータのスイープでは、書籍の設定を採用します。さあ、ランダムウォークのセットアップで両方のアルゴリズムを実行して、そのパフォーマンスを確認しましょう。

結果

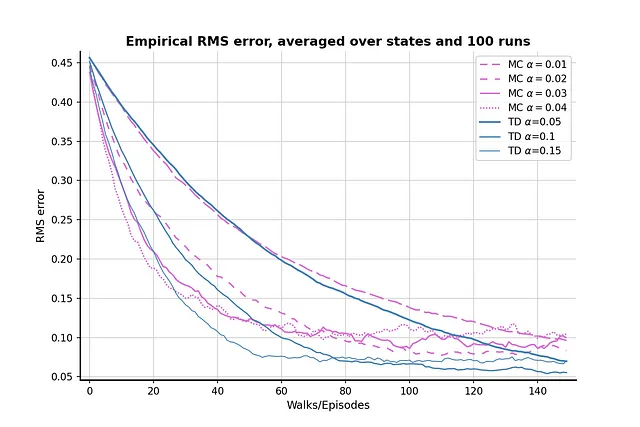
比較を100回行った結果は、上記の画像のとおりです。TD法は一般的にMC法よりも優れた値の推定値を提供し、α = 0.05のTD法は真の値に非常に近い結果を得ることができます。グラフはまた、MC法がTD法に比べて分散が大きいことを示しており、オーキッドの線がスチールブルーの線よりも変動が大きいことがわかります。

両方のアルゴリズムにおいて、αが（比較的）高い場合、RMS損失は最初に減少し、そして再び増加する現象が見られます。このような現象は、値の初期化とαの値の組み合わせ効果によるものです。われわれは比較的高い値0.5を初期値として設定しましたが、これはノードAとBの真の値よりも高い値です。ランダムな方策により、「間違った」ステップを選択する確率が50％あり、エージェントを正しい終端状態から遠ざけるため、より高いα値は間違ったステップを強調し、結果を真の値から遠ざけることにもなります。

では、初期値を0.1に減らして比較をもう一度実行し、問題が緩和されるかどうかを見てみましょう：

低い初期値は明らかに問題を緩和するのに役立ちます。顕著な「下降してから再び上昇する」効果はありません。ただし、初期値が低いと学習効率が低下する副作用があります。RMS損失は150エピソード後も0.05を下回りません。したがって、初期値、パラメータ、およびアルゴリズムのパフォーマンスの間にはトレードオフが存在します。

バッチトレーニング

この記事で最後に触れたいのは、両方のアルゴリズムでのバッチトレーニングの比較です。

以下のような状況を考えてみましょう：ランダムウォークのタスクでの経験を限られた数しか蓄積していない、もしくは時間と計算の制限により一定数のエピソードしか実行できないという状況です。バッチ更新 [2] のアイデアは、既存の軌跡をフルに活用することで、このような状況に対処するために提案されました。

バッチトレーニングのアイデアは、値を一連の軌跡のバッチで繰り返し更新し、値が収束するまで更新を行うことです。バッチの全ての経験が処理されるまで値は更新されません。ランダムウォーク環境で両方のアルゴリズムにバッチトレーニングを実装して、TD法がMC法よりも優れているかどうかを見てみましょう。

結果

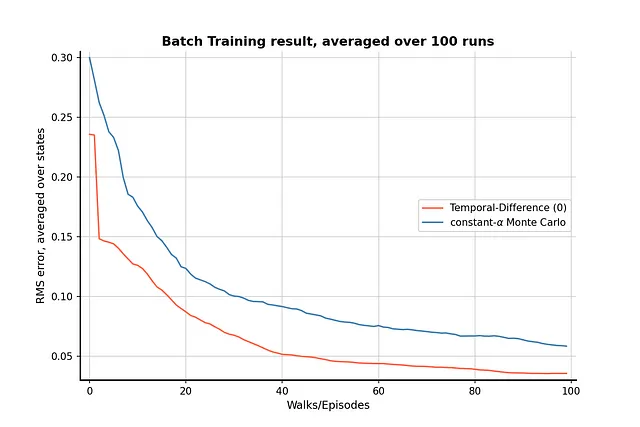
バッチトレーニングの結果、TD法が限られた経験でもMC法よりも優れており、両方のアルゴリズムのパフォーマンスの差は明らかです。

結論

この記事では、定数αのMC法とTD(0)法の違いを説明し、ランダムウォークタスクでのパフォーマンスを比較しました。この記事のすべてのテストでTD法がMC法を上回っているため、強化学習タスクにおいてTD法を考慮することが望ましい選択肢となります。ただし、TD法が常にMC法よりも優れているわけではありません。MC法の最も明らかな利点はバイアスがないことです。バイアスに対して耐性のないタスクに直面している場合は、MC法の方がより良い選択肢になるかもしれません。それ以外の場合は、一般的なケースに対してはTD法の方が適しています。

参考文献

[1] Midjourney Terms of Service: https://docs.midjourney.com/docs/terms-of-service

[2] Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction. MIT Press, 2018.

この記事のGitHubリポジトリ：[リンク]

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!