情報とエントロピー
情報とエントロピー' (Information and Entropy)
説明するための「なぜ、何、そしてどのように」

「エントロピー」を使えば、議論には絶対に負けないと、フォン・ノイマンはシャノンに伝えました。誰も「エントロピー」という言葉の意味を本当に理解していないからです。
— ウィリアム・パウンドストーン
少し歴史から始めましょう。
1948年、クロード・E・シャノンという数学者が「通信の数学的理論」という論文を発表し、機械学習における重要な概念であるエントロピーを紹介しました。
- クロマに会ってください:LLMs用のAIネイティブオープンソースベクトルデータベース-メモリを使用したPythonまたはJavaScript LLMアプリをより速く構築する方法
- 「大規模言語モデル:現実世界のCXアプリケーションの包括的な分析」
- 「データサイエンスとビジネスアナリティクスを学び、イノベーションと成長を推進しましょう」
エントロピーは物理学においては無秩序さを測るものですが、情報理論においては意味が変わります。しかし、どちらも無秩序さや不確実性を評価します。
では、「情報」とは何なのか、掘り下げてみましょう。
I. シャノンの情報
この論文によれば、イベントが伝える情報を定量化することができ、それは「驚き」のレベルを測ることと解釈することができます。情報の内容は、イベントに含まれる驚きの程度を表します。
例を挙げてみましょう:ある人が「動物は水を必要とする」と言ったとします。この文を聞いたとき、どれくらい驚きますか?
驚かないでしょうね。なぜなら、それはよく知られた真実であり、常に真実です。この場合、驚きの量は0に等しく、伝えられる情報も0となります。
しかし、もし誰かが「コインを投げて裏が出た」と言ったらどうでしょう?このイベント(裏が出ること)は確定ではありませんよね。常に表か裏かの50-50の確率があります。そのため、この発言を聞いたときにはある程度の驚きが生まれるかもしれません。ここに確率と驚きの興味深い関係があります。イベントが絶対に起こる(確率1)場合、驚きの度合いは減少します(0になります)。逆に、確率が減少するほど(つまり、イベントがより起こりにくくなるほど)、驚きの感覚は高まります。これが確率と驚きの反比例の関係です。
数式的には

ここで、p(x)はイベントxの確率です。
情報は驚きの量にすぎません。そして、ここで数学を使おうとしているので、「驚き」という言葉を「情報」と置き換えることができます。
information = 1/p(x)とするとどうでしょう?
いくつかの特殊な場合を見てみましょう:
p(x) = 0のとき、information = 1/0 = ∞(無限/未定義)になります。この結果は私たちの直感と一致します:不可能と考えられたイベントが起こった場合、無限または未定義の驚き/情報が生じます。(不可能なシナリオ) ➟ ✅
p(x) = 1のとき、information = 1/1 = 1となり、私たちの観察結果とは矛盾します。絶対に起こりうるイベントの場合、驚き/情報はゼロであるべきです。
➟ ❌
幸いなことに、対数関数が役立ちます。(この記事では一貫して、log₂をlogと表記します。)
情報 = log ( 1/p(x) ) = log(1) — log( p(x) ) = 0 — log( p(x) )
情報 = -log( p(x) )
この新しい式をいくつかの特殊な場合で見てみましょう:
p(x) = 0の場合、information = -log( 0 )= ∞ ➟ ✅
p(x) = 1の場合、information = -log(1) = 0となり、確かに望ましい結果です。絶対に起こりうるイベントは驚き/情報を持つべきではありません。
➟ ✅
イベントによって伝達される驚きや情報量を測定するために、以下の式を使用することができます:

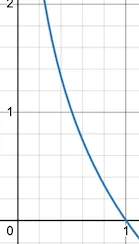
この-log関数は、x = 1のときに0を返します(確率が1の場合、情報は0です)。xが減少すると、対応するy値が急激に増加します。x = 0の場合、情報は無限または未定義になります。この曲線は情報に対する私たちの直感的な理解を正確に捉えています。
そして、一連のイベントに対しては、次のようになります:

これは各イベントの情報の合計であり、情報の単位は「ビット」です。別の直感的な視点をご覧ください:
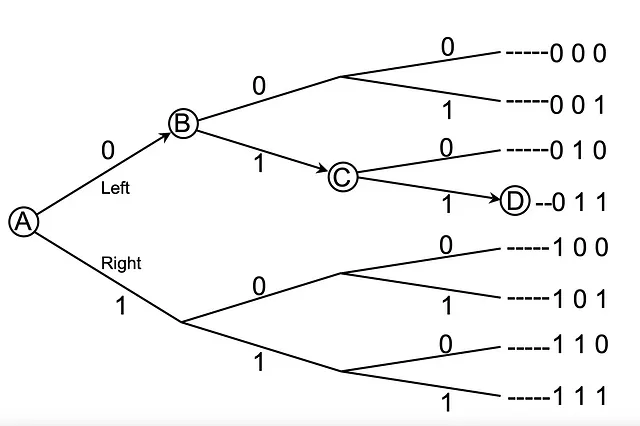
点Aにいて点Dに到達したいとします。ただし、ルートについての情報は全くわからず、隣接するポイントも見えません。さらに、後戻りもできません。
Aにいる間、左(0)と右(1)の2つの選択肢があります。私はあなたに1ビットの情報、つまり0を送ります。これにより、2つの選択肢から選ぶことができます(2番目の列)。Bに到着すると、1のビット値を提供し、合計で2ビットになります。これにより、2 * 2 = 4つのオプションから選ぶことができます(3番目の列)。Cに進むと、さらに1を送り、合計で3ビットになります。これにより、2 * 2 * 2 = 8つのオプションから選ぶことができます(最後の列)。興味深いことに、1は2の対数、2は4の対数、3は8の対数です。
「n」ビットの情報を入手すると、「m」の選択肢から選ぶことができます。
例えば、8 = 2³(m = 8は可能な合計の結果を表し、n = 3はビットの数を表します)
一般的には、
m = 2ⁿ

これは情報(有用なビットの数)のための方程式です。
情報理論の基本的な直感は、起こりにくいイベントが発生したことを学ぶことは、起こりやすいイベントが発生したことを学ぶよりも情報が多いということです。
— 『Deep Learning, 2016』, 73ページより引用
II. エントロピー
与えられたリスト[1, 2, 3, 4]から確率分布を使用してランダムな数値を生成したい場合を考えてみましょう。
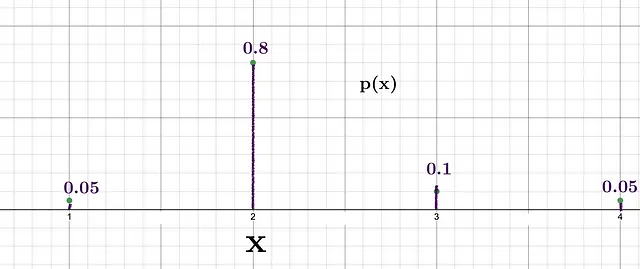
2を取得する確率が最も高いことがわかります。つまり、2を得たときの驚きの度合いは、確率0.1の3を得たときの驚きと比べて比較的低いです。これら2つのイベントのシャノン情報は:
- 2の情報 = -log(0.8) = 0.32ビット
- 3の情報 = -log(0.1) = 3.32ビット
各数値を生成するたびに、得られる情報は異なることに注意してください。
提供された分布に従ってこの生成プロセスを100回実行すると、個別のインスタンスで得られた情報を合計する必要があります。
1を生成する観測回数 = 0.05 * 100 = 5
2を生成する観測回数 = 0.8 * 100 = 80
3を生成する観測回数 = 0.1 * 100 = 10
4を生成する観測回数 = 0.05 * 100 = 5
では、100回の生成によって伝えられる総情報を計算しましょう。
1を5回生成したときの得られる情報 = — log(0.05) * 5 = 21.6 bits
2を80回生成したときの得られる情報 = — log(0.8) * 80 = 25.8 bits
3を10回生成したときの得られる情報 = — log(0.1) * 10 = 23.2 bits
4を5回生成したときの得られる情報 = — log(0.05) * 5 = 21.6 bits
総情報 = 92.2 bits
したがって、100の観測によって伝えられる総情報は92.2 bitsです。
もしも観測ごとの情報量(平均)を計算できたら素敵でしょうね。
上記分布の平均情報 = 92.2 / 100(100回の観測があったので)
平均情報 = 0.922 bits
イエス、これが私たちがエントロピーと呼ぶ量です。
ここには特別なことはありません。確率分布によって伝えられる平均(期待される)情報量です。さあ、エントロピーの式を導出しましょう。

p(x) × N は、N回の観測が行われたときにイベントxが発生する回数です。
したがって、最終的な一般的な方程式は次のようになります。

Hはエントロピー、Eは期待値です。
私のAIと数学に関する投稿をフォローしてください。
参考文献
[1] C. E. SHANNON, “A Mathematical Theory of Communication”, 1948
[2] Josh Stramer, “Entropy (for data science) Clearly Explained!!!”, Youtube, 2022
[3] James V Stone, “Information Theory: A Tutorial Introduction”, 2018
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
