「大数の法則の解明」

大数の法則の解明

LLNが興味深いのは、言っていないことと言っていることの両方のためです

1966年8月24日、才能ある劇作家トム・ストパードはスコットランドのエディンバラで劇を上演しました。その劇のタイトルは「ローゼンクランツとギルデンスターンは死んだ」。中心となるキャラクター、ローゼンクランツとギルデンスターンは、シェイクスピアの名作「ハムレット」の幼馴染です。劇はギルデンスターンが繰り返しコインを投げる場面で始まりますが、そのコインは頭の部分が出続けます。各結果で、ギルデンスターンの財布は軽くなり、ローゼンクランツの財布は重くなります。頭が続くドラムビートによって、ギルデンスターンは心配になります。彼は自分が何か遠い昔の罪のために自らのコインがすべて頭になるように願っているのではないかと心配しています。または最初のコインを投げた後に時間が止まり、彼とローゼンクランツが同じ結果を何度も繰り返しているのかもしれません。

ストパードは、確率の法則が私たちの世界観、期待感、人間の思考の本質に組み込まれていることを見事に示しています。92回目のコイン投げも頭になったとき、ギルデンスターンは、確率の法則がもはや働かない非自然な現実の支配下にあるのではないかと尋ねます。

ギルデンスターンの恐怖はもちろん根拠のないものです。連続して92回も頭になる確率は想像を絶するほど小さいです。実際、それは小数点の後に28個のゼロ、そして2が続く数です。ギルデンスターンが隕石に当たる確率の方が高いです。

ギルデンスターンは、翌日に戻ってきて別の92回のコイン投げをすれば、結果はほぼ確実に大きく異なるものになるでしょう。彼が毎日このルーティンを続ければ、ほとんどの日に頭の数と裏の数がほぼ一致することがわかるでしょう。ギルデンスターンは、私たちの宇宙が示す魅力的な振る舞い、つまり「大数の法則」を経験しています。

• Plotly Expressを使用してマップをアニメーション化する
• LLaMA 皆のためのLLM！
• 「国連機関がロボットのグループを組織し、AIの未来についての議論を引き起こす」

大数の法則を平易な英語で説明する

大数の法則（LLN）には弱いバージョンと強いバージョンの2つが存在します。弱いLLNは直感的で理解しやすいかもしれませんが、誤解される可能性もあります。この記事では弱いバージョンについて説明し、強いバージョンについての議論は別の記事で行います。

弱い大数の法則は、サンプル平均と母集団平均の関係に関心を持ちます。以下、平易な文章で説明します：

ある特定のサイズ（例えば100）の母集団から無作為なサンプルを抽出するとします。ちなみに、用語「サンプルサイズ」を心に留めておいてください。サンプルの「サイズ」は、この法則のリングマスター、グランドプーバの役割を果たします。次に、このサンプルの平均を計算して別のところに置きます。そして、このプロセスを何度も繰り返します。すると、不完全な平均値のセットが得られます。これらの平均値は不完全です。なぜなら、それらと真の母集団平均の間に常に「ギャップ」、デルタ、偏差があるからです。ある程度の偏差を許容すると仮定しましょう。このセットから無作為にサンプル平均を選ぶと、サンプル平均と母集団平均の絶対的な差が選択した許容範囲を超える可能性があります。

弱い大数の法則は、サンプルサイズが無限大または母集団のサイズに成長するにつれて、この偏差が選んだ許容レベルを超える確率がゼロに近づくと述べています。

選んだ許容レベルがどれほど小さくても、サンプルのサイズを増やしていくにつれて、セットから無作為に選んだサンプルの平均がこの許容範囲を超える可能性はますます低くなります。

弱いLLNがどのように機能するかの実世界の例

弱いLLNがどのように機能するかを見るために、例を通して実行してみましょう。それには、もしよろしければ、北大西洋の冷たく陰鬱な広がりに連れて行っていただきます。

アイルランド政府は、北東北大西洋の水面から測定された水温のデータセットを毎日公開しています。このデータセットには、緯度と経度でインデックスされた数十万の水面温度の測定値が含まれています。例えば、2023年6月21日のデータは以下の通りです：

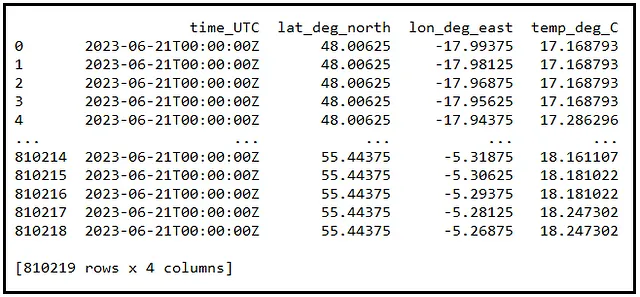
８０万の水温値を想像するのは少々難しいですね。そこで、このデータを視覚化するために散布図を作成しましょう。以下にそのプロットを示します。プロット内の白い空白地帯はアイルランドとイギリスを表しています。

統計学の学生として、あなたは「母集団」にアクセスすることはありません。ですので、私がこの８０万の温度測定値を「母集団」と呼ぶことについては、きっぱりと非難されても正しいです。しかし、少しの間お付き合いください。すぐに理解できるようになるでしょう。なぜなら、LLNを理解するためには、このデータを「母集団」として考えることが役に立つからです。

では、このデータがあくまで「あのぅ…咳」…「母集団」だと仮定しましょう。この８１０２１９箇所のデータの平均水温は17.25840度 Celsiusです。17.25840は単に８１０Kの温度測定の平均です。この値を母集団平均μとします。この値を覚えておいてください。頻繁に参照する必要があります。

では、この８１０２１９の値の「母集団」にはアクセスできないと仮定しましょう。代わりに、この「母集団」からランダムに抽出したたった２０のサンプルのみにアクセスできるとします。以下に一つのランダムサンプル例を示します：

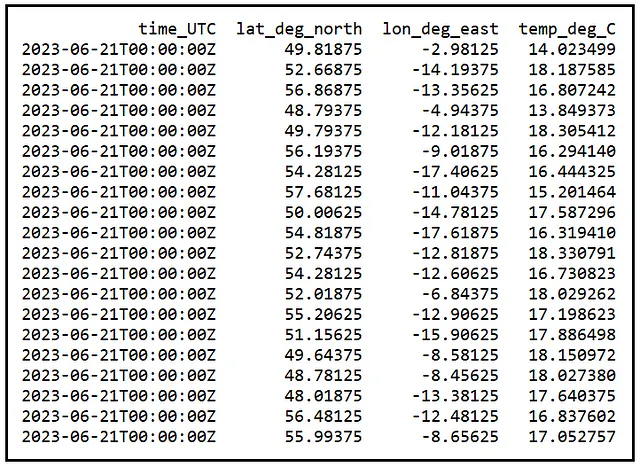
このサンプルの平均温度は16.9452414度 Celsiusです。これが私たちのサンプル平均X_barであり、以下のように計算されます：

X_bar = (X1 + X2 + X3 + … + X20) / 20

同じ「母集団」から２０個のサンプルを簡単に２つ目、３つ目、実際には任意の数だけ抽出することができます。以下にいくつかのランダムサンプル例を示します：

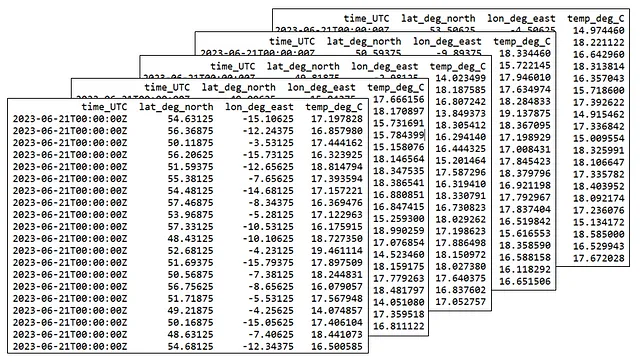
ランダムサンプルの真の意味についてのちょっとした補足

さて、先に進む前に、ランダムサンプルの概念を少し見てみましょう。これによって、弱いLLNの仕組みが理解しやすくなります。そして、この視点を得るために、カジノのスロットマシンを紹介しなければなりません：

上記のスロットマシンには３つのスロットがあります。マシンのアームを回すたびに、マシンは内部で保持している果物のリストなどの画像の母集団からランダムに選ばれた画像で各スロットを埋めます。今度は、X1からX20という名前の２０のスロットを持つスロットマシンを想像してください。このマシンは、８１０２１９個の温度測定値の母集団から値を選ぶように設計されています。アームを引くと、２０個のスロットX1からX20がそれぞれ８１０２１９個の値の母集団からランダムに選ばれた値で埋まります。したがって、X1からX20はそれぞれ母集団からの任意の値を保持するランダム変数です。言い換えれば、ランダムサンプルの各要素自体がランダム変数です。

X1からX20までにはいくつかの興味深い特性があります:

• X1が取る値は、X2からX20が取る値とは独立です。同様に、X2、X3、…、X20も独立です。したがって、X1からX20は独立なランダム変数です。
• X1、X2、…、X20は、それぞれが母集団の任意の値を保持できるため、それぞれの平均は母集団の平均μです。期待値を表す記号E()を使用して、この結果を以下のように表します: E(X1) = E(X2) = … = E(X20) = μ。
• X1からX20は同一の確率分布を持ちます。

したがって、X1、X2、…、X20は独立で同一分布の（i.i.d.）ランダム変数です。

…そして今、弱いLLNがどのように機能するかを示すことに戻りましょう

この20要素のサンプルの平均（X_barで表される）を計算して別の場所に置いておきましょう。そして、再び機械のアームを回して20要素のランダムサンプルが出てきます。その平均を計算し、それを別の場所に置きましょう。このプロセスを1000回繰り返すと、1000個のサンプル平均が計算されます。

以下は、この方法で計算された1000個のサンプル平均の表です。それらをX_bar_1からX_bar_1000と指定します:

ここで次の声明を注意深く考えてください:

サンプル平均はランダムなサンプルから計算されるため、サンプル平均自体がランダム変数であるということです。

この時点で、もし頭をうなずかせていて、あごを撫でているなら、それはまさに正しいことです。サンプル平均がランダム変数であるということは、統計学で持つことができる最も深い洞察の1つです。

また、上の表の各サンプル平均が母集団平均μから一定の距離にあることにも注意してください。これらのサンプル平均のヒストグラムをプロットして、μの周りにどのように分布しているかを見てみましょう:

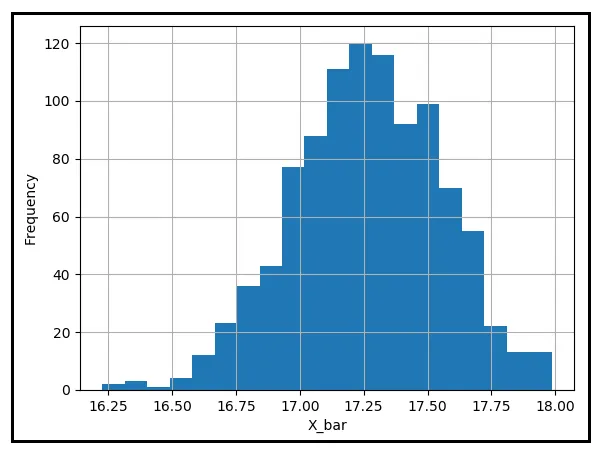
サンプル平均の大部分は、17.25840度の摂氏という母集団平均に近い位置にあるようです。ただし、μからかなり離れたものもあります。この距離に対する許容範囲が0.25度摂氏であると仮定しましょう。もしバケツの中に1000個のサンプル平均が入っていて、その中から手を伸ばして手に入れる平均値を取り出すとします。この平均値とμの絶対値の差が0.25度摂氏以上である確率はどれくらいになるでしょうか？この確率を推定するためには、μから0.25度以上離れたサンプル平均の数を数え、この数を1000で割ります。

上記の表では、この数が422であり、したがって確率P(|X_bar — μ | ≥ 0.25)は422/1000 = 0.422となります。

この確率を一時的に置いておきましょう。

今度は、サンプルサイズを20ではなく100にして、上記の手順をすべて繰り返してみましょう。つまり、サイズ100のランダムなサンプルを1000回抽出し、各サンプルの平均を取り、それらの平均を保存し、μから0.25度摂氏以上離れたものの数を数え、この数を1000で割ります。これがヘラクレスの労働のように聞こえる場合、それは間違いではありません。少し休憩して息を整える時間を取ってください。そして、一通りの作業を終えた後に、自分の労苦の成果が以下のようになったことに気づいてください。

以下の表には、1000個のランダムサンプルの平均値が含まれています。各サンプルのサイズは100です：

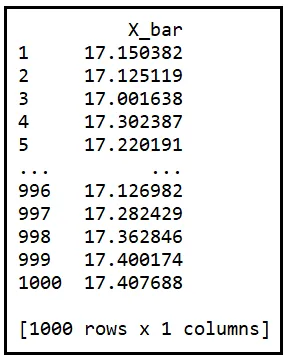
この1000個の平均値のうち、56個の平均値がμから最低0.25度Cずれています。これにより、このような平均値に出会う確率は56/1000 = 0.056となります。この確率は、サンプルサイズが20の場合に計算した0.422よりも明らかに小さいです。

これらの手順を複数回繰り返し、毎回サンプルサイズを増やしていくと、確率の表が得られます。私はサンプルサイズを10から490まで10ずつ増やしてこの演習を行いました。以下がその結果です：

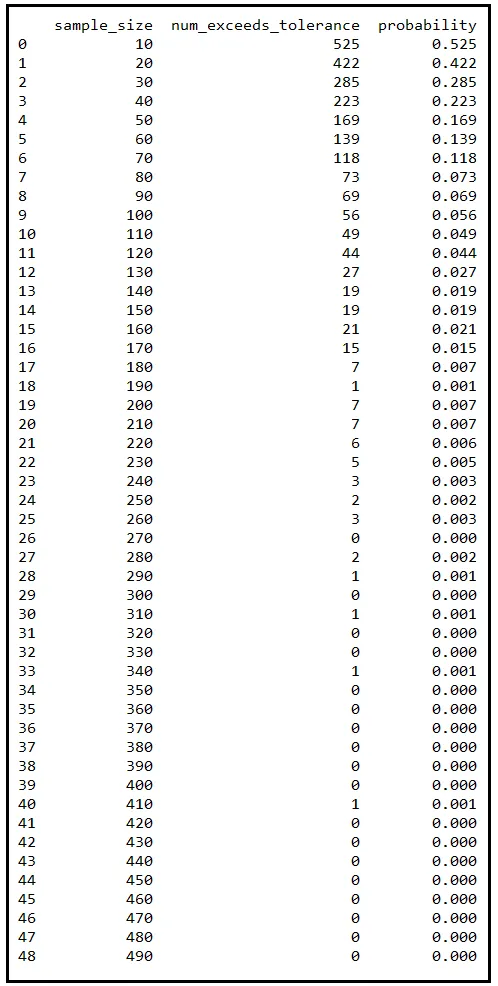
この表の各行は、810219個の温度測定結果の集団からランダムに抽出した1000個の異なるサンプルに対応しています。 sample_size 列には、これら1000個のサンプルのサイズが記載されています。抽出後、各サンプルの平均値を取り、μから最低0.25度Cずれているものの数を数えました。 num_exceeds_tolerance 列には、この数が記載されています。 probability 列は num_exceeds_tolerance / sample_size です。

サンプルサイズが増えるにつれて、この数は急速に減少していくことに注意してください。同様に、対応する確率 P(|X_bar — μ | ≥ 0.25) も減少していきます。サンプルサイズが320に達すると、確率はゼロに減衰します。時折0.001に上昇することもありますが、これは有限な数のサンプルを描いたためです。サンプルを1000個ではなく10000個ずつ描くと、たまに上昇する部分は平らになり、確率の減衰もより滑らかになります。

次のグラフは、確率 P(|X_bar — μ | ≥ 0.25) をサンプルサイズに対してプロットしたものです。サンプルサイズが大きくなるにつれて、確率がゼロに急降下することがはっきりと示されています。

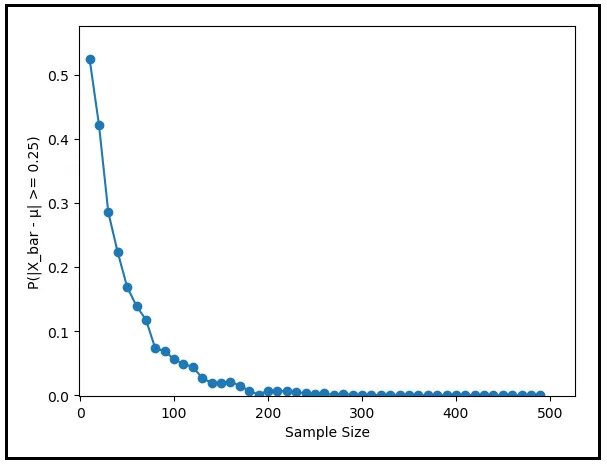
0.25度Cの代わりに、異なる許容値（より低い値またはより高い値）を選んだ場合はどうなるでしょうか？選択した許容レベルにかかわらず、確率 P(|X_bar — μ | ≥ ε) はサンプルサイズが増えるにつれて常にゼロに収束します。これが大数の法則（Law of Large Numbers）の働きです。

弱法則の形式的な述べ方

弱法則の振る舞いは以下のように形式的に述べることができます：

X1、X2、…、Xn が i.i.d.（独立同分布）の確率変数で、n 個のランダムサンプルを形成するとします。このサンプルの平均を X_bar_n とします。また、E(X1) = E(X2) = … = E(Xn) = μ とします。このとき、非負の実数 ε に対して、サンプルのサイズが無限に近づくとき、X_bar_n が μ から ε 以上離れる確率はゼロに近づきます。以下の優れた方程式がこの振る舞いを捉えています：

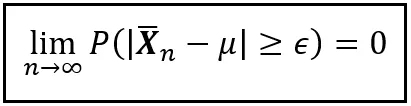
この法則の310年の歴史の中で、数学者たちは X1 から Xn が独立同分布であるという要件を徐々に緩和しながら、法則の本質を保ち続けることができました。

「確率収束の原理」、plim記法、そして極めて少ない言葉で非常に重要なことを表現する技術

確率を輸送手段としてある値に収束する特定のスタイルを「確率収束」と呼びます。一般的には以下のように述べられます：

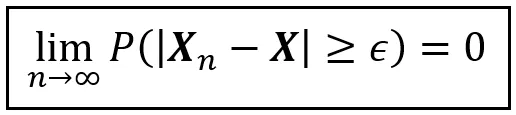
上記の方程式で、X_n と X は確率変数です。ε は非負の実数です。この方程式は、n が無限に近づくとき、X_n が確率収束して X に収束することを述べています。

統計学の広大な領域全体で、あなたは「plim」という控えめな記法に何度も出くわすことでしょう。それは「p lim」と発音されます。または「plim」とも（「plum」という言葉と同じように発音されますが「i」が入ります）。また、確率極限とも呼ばれます。plimは、ある尺度（たとえば平均）が特定の値に「確率収束する」ということを短い形式で表現する方法です。plim を使用することで、弱法則の形式的な表現は次のように簡潔に述べることができます：

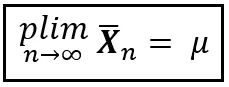
または単純に：

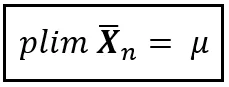
この記法の簡潔さは驚くべきものです。数学者は簡潔さに惹かれるものです。深遠な真理を伝える際に、数学は最もインク効率の良い分野かもしれません。そして、この効率主義に執着する分野の中で、plimはトップの位置を占めます。plimと同じ意味をより少ないインクや電子で表現するような深遠な概念を見つけるのは困難でしょう。

しかし、もうこれ以上苦労することはありません。plimの簡潔な美しさに物足りなさを感じた場合、同じ意味を伝える可能性のある、さらに効率的な記法があります：

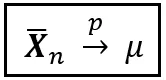
弱い大数の法則についての迷信を打ち砕く

この記事の冒頭で、弱い大数の法則が何を言わないかという点が注目されると述べました。それについて説明します。弱い大数の法則は、サンプルサイズが増えるにつれてその平均が母集団の平均またはその概念のいくつかに近づくと誤解されることがよくあります。しかし、我々が見たように、弱い大数の法則に関するそのような考えは現実とは何の関係もありません。

実際には、弱い大数の法則に関するいくつかの神話をすぐに打ち破りましょう。

神話＃1：サンプルサイズが増えると、サンプル平均は母集団平均に収束する。

これはおそらく弱い大数の法則の最も頻繁な誤解です。しかし、弱い大数の法則はそのような主張をしていません。それがなぜなのかを理解するために、次の状況を考えてみてください：非常に大きなサンプルを手に入れることに成功しました。その成果を喜んで称賛する一方で、次の質問を自分自身に投げかけるべきです：サンプルが大きいからと言って、それがバランスの取れたものでなければならないのでしょうか？自然が巨大なバイアスを含んだ巨大なサンプルであなたを打ちのめすことを防いでいるものは何もありません。実際に、ギルデンスターンは92回の表の連続のシーケンスでそれが完全にランダムなサンプルであったのではありませんか？もしそれが大きなバイアスを持っている場合、それにもかかわらずサンプルサイズが大きくても、バイアスは真の母集団の値からはるかに離れた点までサンプル平均を吹き飛ばすでしょう。逆に、小さなサンプルは極めてバランスの取れたものであることが証明されるかもしれません。ポイントは、サンプルサイズが増えるにつれて、サンプル平均が母集団平均に忠実に近づくことが保証されているわけではないということです。自然はそんな不必要な保証を提供しません。

神話＃2：サンプルサイズが増えると、サンプルのほぼすべての要素 — 中央値、分散、標準偏差 — はそれぞれの母集団の値に収束する

この文は、1つの持ち運びに便利なパッケージにまとめられた2つの神話です。まず第一に、弱い大数の法則は確率収束を仮定しており、値の収束ではありません。第二に、弱い大数の法則はサンプル平均の確率収束にのみ適用され、他の統計量の収束には触れていません。中央値、分散、標準偏差など、他の測定値の収束については弱い大数の法則は言及していません。

弱い大数の法則が成立するかどうかを知る方法

弱い大数の法則を述べ、実世界のデータを使用してその動作を実証することは一つのことです。しかし、それが常に機能することを確認する方法はありますか？サンプル平均が確率的に母集団の値に収束しない場合がある状況はありますか？それを知るためには、弱い大数の法則を証明し、それが適用される条件を正確に定義する必要があります。

実際には、弱い大数の法則には美味しそうな証明があり、その一部として、絶えず興味をそそられるチェビシェフの不等式を使用しています。もし興味があれば、次の記事で弱い大数の法則の証明についてお楽しみにしてください。

ギルデンスターンを再訪する

このトピックを取り上げる際に、友人であるギルデンスターンの心配を安心させずにはお帰りになるのは失礼でしょう。彼が経験した結果がどれほど非常に起こりにくいものであったかを理解しましょう。擬似乱数生成器を使用して92枚の公正なコインを投げる行為をシミュレートします。表が1、裏が0とエンコードされます。92回の結果の平均値を記録します。平均値は、コインが表になる回数の割合です。この実験を1万回繰り返して、92回のコイン投げの1万個の平均値を取得し、その頻度分布をプロットします。この演習を完了した後、次のようなヒストグラムプロットを得ることができます：

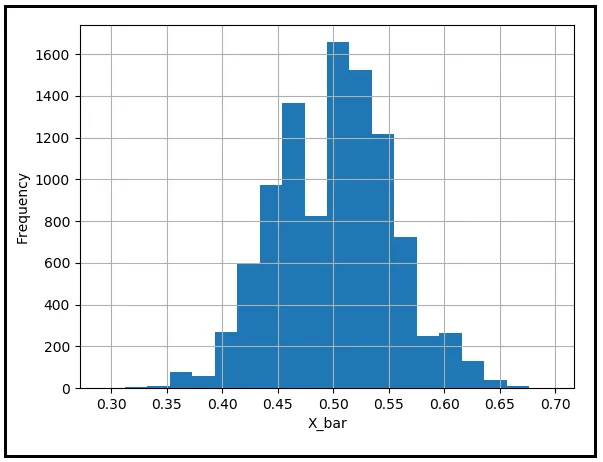
ほとんどのサンプル平均が0.5の母集団平均の周りに集まっていることがわかります。ギルデンスターンの結果である92回の表が連続することは、非常に起こりにくい結果です。したがって、この結果の頻度は非常に小さいです。しかし、ギルデンスターンの恐れに反して、この結果には何の不自然さもなく、確率の法則は通常の勢いで運営し続けます。ギルデンスターンの結果は単にプロットの左側の遠隔地域に潜んでおり、想像を絶するほど不運な人間に襲いかかるために無限の忍耐を持って待っています。

参考文献と著作権

データセット

CC BY 4.0の下、DATA.GOV.IEからダウンロードしたノースイースト大西洋リアルタイム海面温度データセット

画像

この記事のすべての画像は、別の出典と著作権が画像の下に記載されていない限り、Sachin Dateの著作権によるCC-BY-NC-SAです。

お読みいただきありがとうございます！この記事が気に入った場合は、フォローしていただくと、回帰分析や時系列分析に関するヒント、方法、プログラミングのアドバイスを受け取ることができます。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!