多段階回帰モデルとシンプソンのパラドックス
多段階回帰モデルとシンプソンのパラドックス
適切なツールを使って誤った結論を避ける
データ分析は、その職業名が示すように、データサイエンティストの仕事の重要な部分であり、記述統計や単純な回帰モデルから洗練された機械学習手法まで様々なアプローチがあります。しかし、これらのアプローチは注意深く扱う必要があり、適切なアプローチを選択することは簡単ではありません。複雑なデータには、適切に考慮されない場合には無効な結論につながる可能性がある隠れた構造が含まれていることがよくあります。
この記事では、シンプソンのパラドックスの例を示し、単純で短視眼的な分析が、データに裏付けられたように見えるが、実際には誤解に過ぎない誤った結論につながる方法を紹介します。これにより、多レベル回帰モデルの使用方法を示し、階層的なデータに対する適切なデータ分析手法を示します。
問題
さあ、始めましょう!私たちはスマートフォンアプリを公開し、ユーザーについてもっと知りたいと思っています。そのため、小規模な調査を行い、ユーザーにアプリの満足度を1(非常に不満)から4(非常に満足)のスケールで教えてもらいます。さらに、直近の1週間にアプリ内で過ごした時間を計測し、豊富なサンプルを得るために、異なる国のユーザーにも尋ねました。その結果、データは次のようになります(この記事では生成されたデータを使用しています):
満足度 時間 国0 2.140440 1.585295 01 2.053545 0.636235 02 1.589258 1.468033 13 1.853545 0.968651 24 1.449286 0.967104 2. . . .. . . .. . . .私たちは、アプリ内で過ごした時間と報告された満足度の関係に興味があります。具体的には、アプリ内での時間が長いほど満足度が高いのか低いのかを知りたいのです。そして、その関連性を定量化したいのです。つまり、「アプリ内で1時間過ごすことは、満足度がx倍高くなる/低くなる」というような声明をしたいのです。データを見ると、アプリ内での時間が長いほど満足度が低くなるという第一の直感があるかもしれません。
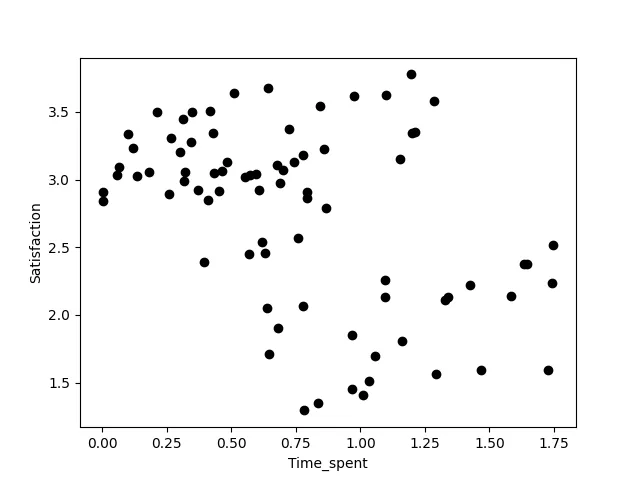
線形回帰
さあ、線形回帰を行って、私たちの直感が正しいかどうか確認しましょう。線形回帰では、時間の経過に伴う満足度を予測するために、満足度=切片+回帰係数*時間の形式の線形関数として予測を行います。statsmodelsパッケージを使用して、OLS(Ordinary Least Squares)関数を使って簡単に行うことができます。
import statsmodels.api as smresult = sm.OLS(df["満足度"], sm.add_constant(df["時間"])).fit()print(result.params)add_constantメソッドは、モデルに、方程式に切片を含めたいことを伝えるための技術的な詳細です(データが標準化されていない限り、これは必要です)。result.paramsは2つの値を返します。切片(const)と変数時間の回帰係数です。
const 3.229412時間 -0.655470つまり、私たちのモデルは、満足度を3.229–0.655*時間として予測すると言っています。つまり、アプリ内で1時間以上過ごすと、満足度が0.655ポイント減少します(マイナスの符号のため)。ただし、最初の印象(時間=0)からの人々の平均的な満足度は3.229です。これを、切片3.229と傾き-0.665の直線で可視化することもできます:
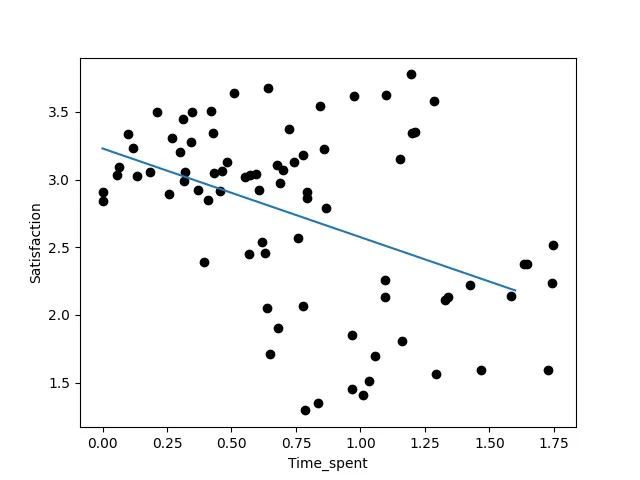
もちろん、この予測は完璧ではありませんが、少なくとも傾向を示してくれます。では、ケースは明確ですか?アプリでの時間を増やすと満足度が低下するという結論が得られましたし、その低下を数値化することもできました。それに基づいてアプリの改善策を考えたり(もちろん、ユーザーがアプリを使用するにつれて満足度が高まることを望んでいます)、なぜユーザーが満足していないのかをより詳細に調査したりすることができます。
しかし、そこまで急がないでください!
国ごとのグループ化
覚えているでしょうか、私たちは異なる国のユーザーからデータを収集しました。では、国ごとにデータを見てみるとどうなるでしょうか?次のプロットでは、前と同じデータポイントを見ることができますが、今回は各国を異なる色で強調しています。
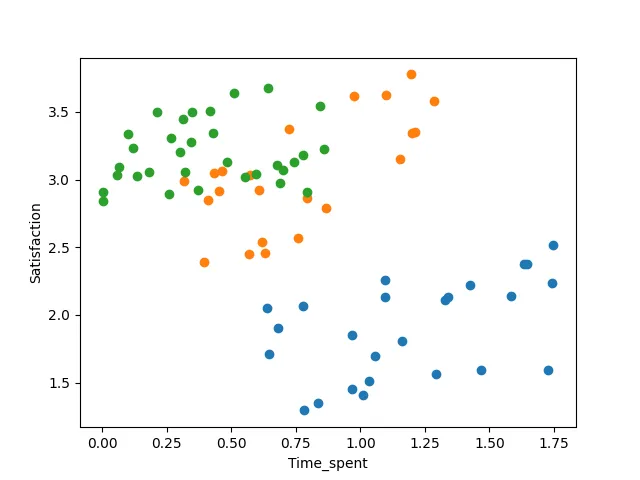
このプロットから2つの観察結果が得られます。まず、国によって満足度とアプリでの時間が異なるようです。青い国の被験者は他の国の被験者よりもアプリでの時間が長いですが、平均的には満足度が低いです。さらに、3つの国を個別に見ると、アプリでの時間と満足度の関連性が実際には正の傾向があるように思えるかもしれません。これは以前の分析と矛盾しているのではないでしょうか?
シンプソンの逆説
私たちが見た効果はシンプソンの逆説と呼ばれます。これは、データの相関がグループ間とグループ内で異なる場合に発生します。非常に直感に反するかもしれませんが、これは実際に起こります(私たちが見たように)し、その原因は交絡変数です。私たちの例で説明しましょう。各国を個別に見ると、正のトレンドが見られます:アプリでの時間が長いほど満足度も高くなります。しかし、すでに見たように、国は満足度とアプリでの時間の平均が異なります。青い国では、平均満足度は低いですが、平均アプリでの時間はオレンジや緑の国よりも長いです。これは国内のトレンドとは逆のトレンドです。ただし、これには別の変数が関与している可能性があります。たとえば、青い国では、より多くの人がより頻繁に退屈しているため、一般的には満足度が低くなり(その結果、アプリへのポジティブな気分が低くなる)が、アプリでの時間を過ごす時間が長くなります。もちろん、これは可能な説明の一つであり、他にも多くの説明が考えられます。ただし、正しい説明は現時点ではあまり重要ではありません。私たちにとって重要なのは、国間には系統的な違いがあるということです。
では、前の分析でそれを見つけることができなかったのはなぜでしょうか?線形回帰を実行する際に間違えたのでしょうか?そうです、線形回帰を実行すること自体が間違っていました。なぜなら、線形回帰の中心的な仮定の1つが違反されていたからです。線形回帰では、すべてのデータポイントが独立に同じ分布からサンプリングされたという仮定がされていますが、私たちの例ではそうではありませんでした。明らかに、アプリでの時間と満足度の分布は、異なる国によって異なります。したがって、線形回帰の仮定が違反されると、線形回帰はデータ分析に適したツールではありません。
階層モデル
では、より適切な方法でデータを分析するためにはどうすればよいでしょうか?幸いなことに、統計モデルは線形回帰のアイデアを階層データに拡張したものが利用できます。私たちは、私たちが質問した人々が国にネストされているような階層的な構造でデータポイントをサンプリングした場合、そのような統計モデルを階層線形モデル、多層モデル、または線形混合効果モデルと呼びます。このようなモデルは、所属するグループ構造を考慮して、固定効果とランダム効果と呼ばれるものを導入します。単純な例では、1つの変数を予測するために1つの他の変数を与えたい場合(私たちはアプリでの時間を与えて満足度を予測したい場合)、固定効果はすべてのグループに対して1つの切片と1つの傾きから構成されます。これまでは線形回帰とまったく同じです。
ランダム効果によって、それぞれのグループごとに切片からのずれが生じることがあります。例えば、青い国の切片は少し低くなり、緑の国の切片は少し高くなるかもしれません。これによって、国ごとの満足度の平均レベルの違いを説明できます。
さらに、ランダム効果は各グループごとに傾きのずれを導入することができます。例えば、オレンジのグループでは、傾きが固定の傾きよりも高くなる(つまり、満足度と経過時間の関連性が強くなる)可能性があり、緑の国では低くなるかもしれません。
階層モデルの実行例
実際にそれを見て、実際に何が起こるのかを理解しましょう。新しい分析を行いますが、今回はstatsmodelsのmixedlm関数を使用します。式「Satisfaction ~ Time_spent」によって満足度を予測することを明示し、データフレームの「Country」列が異なるグループを決定することを示します。さらに、パラメータre_formula=”Time_spent”を指定することで、モデルに各グループごとに個別の傾きを持つように指示します。これがないと、ランダム効果はグループごとの切片のみを考慮し、個別の傾きは考慮しません。
import statsmodels.formula.api as smfresult = smf.mixedlm("Satisfaction ~ Time_spent", data=df, groups=df["Country"], re_formula="Time_spent").fit()print(result.fe_params)print(result.random_effects)fixed_effects(fe_params)とrandom_effectsを出力すると、以下のような値が得られます:
Fixed effects Intercept 2.286638 Time_spent 0.497657Random Effects {0: Group -0.958805, Time_spent -0.018178, 1: Group 0.155233, Time_spent 0.274222, 2: Group 0.803572, Time_spent -0.256044}では、これはどういう意味でしょうか?fixed_effectsでは、切片に1つの値、変数time_spentに1つの値があります。しかし、ランダム効果では、各国(0,1,2)ごとに2つの値があります:切片(Group)と変数の傾き(Time_spent)。先程見たように、ランダム効果は各グループの平均効果からのずれを表しています。3つのグループに対して、切片と傾きそれぞれに固定効果にランダム効果を加えた線形方程式を構築することができます。
satisfaction_0 = (2.286638 - 0.958805) + (0.497657 - 0.018178) * time_spent = 1.327833 + 0.479479 * time_spentsatisfaction_1 = (2.286638 + 0.155233) + (0.497657 + 0.274222) * time_spent = 2.441871 + 0.771879 * time_spentsatisfaction_2 = (2.286638 + 0.803572) + (0.497657 - 0.256044) * time_spent = 3.090210 + 0.241613 * time_spentグループ0のランダム切片は負の値(-0.958)であり、グループ2のランダム切片は正の値(0.803)です。そのため、グループ0は固定切片よりも下にあり、グループ2は上にあります。したがって、グループ0の線形関数では最も低い切片(1.327)があり、グループ2は最も高い切片(3.090)があります。つまり、国0では満足度が国2よりも低いレベルで始まるということです。
また、グループ間で傾きが異なることもわかります。グループ1では、傾きが最も高く、0.771ですが、グループ2では0.241しかありません。つまり、アプリでの経過時間と満足度の関連性は国1では国2よりもはるかに高いです。言い換えれば、国1ではアプリでの1時間の経過時間の増加によって満足度が0.771ポイント増加します(平均的には)、一方、国2では満足度がさらに0.241ポイント増加します。さらに、すべての傾きが正であることもわかります。これは、最初に行った線形回帰の負の傾きとは矛盾しています。
今、各国ごとに1つの回帰線をプロットすることができます:
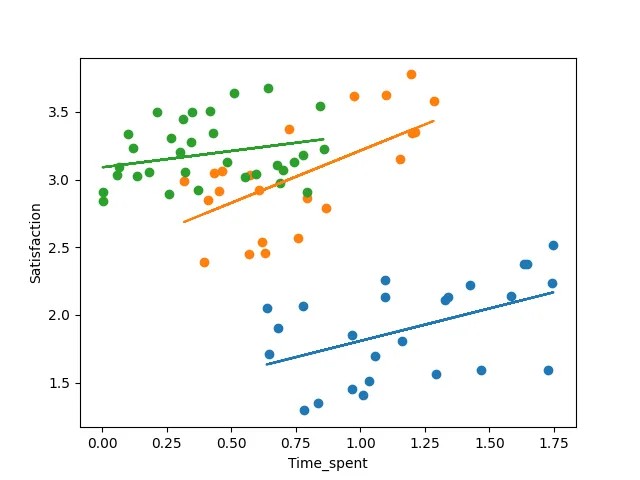
これにより、各国での正の傾向と(つまり、time_spent=0のときの線の位置)の異なる切片を明確に認識できます。
結論
上記の例では、短絡的な分析が容易に誤った結論に導くことができることを見ました。異なる国から来たユーザーなど、データの入れ子構造を無視すると、線形回帰の後に停止してしまい、アプリでの時間の増加と満足度の低下が関連していると結論付けることができました。線形回帰の核となる仮定を満たしていないことを理解することで、同じ分布からサンプリングされたデータ点ではないため、さらなる分析を行う動機づけが生まれ、アプリでの時間の増加が実際に満足度の向上と関連していることが明らかになりました。
したがって、この例から次のような教訓を得ることができます:
- 分析のために統計的な手法を使用する前に、その仮定がデータと一致しているかを検証する必要があります。
- 入れ子構造のあるデータの場合、すべてのデータ点が同じ分布からサンプリングされたという仮定は常に成り立たない場合があります。
- データ全体のトレンドと、それを形作る個々のグループ内のトレンドが異なることがあります。これはシンプソンの逆説と呼ばれます。
- 多層線形モデルは、入れ子構造を持つデータ構造に対処し、シンプソンの逆説からの誤った結論を回避する方法の一つです。
さらなる読み物
私たちは、statsmodelsの階層モデルの以下の実装を使用しました:
- https://www.statsmodels.org/stable/mixed_linear.html
私は以下の統計の教科書を使用しました(残念ながら、ドイツ語のみで利用可能です)。
- Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden.
多層モデルに関する背景情報は、以下で見つけることができます:
- Snijders, T. A. B.; Bosker, R. J. (2011). Multilevel Analysis: an Introduction to Basic and Advanced Multilevel Modeling (2nd ed.). London: Sage. ISBN 9781446254332.
結果を再現したい場合、次のようにデータが生成されました:
import numpy as npimport pandas as pdgroup_1_x = np.random.uniform(0.5, 1.8, 25)group_1_y = (1 + 0.3 * group_1_x) + np.random.rand(len(group_1_x))#start_2, end_2, step_2 = 0.3, 1.3, 0.04group_2_x = np.random.uniform(0.3, 1.3, 22)group_2_y = (2 + 0.7*group_2_x) + np.random.rand(len(group_2_x))#start_3, end_3, step_3 = 0, 1, 0.04group_3_x = np.random.uniform(0, 1, 32)group_3_y = (2.5 + 0.3*group_3_x) + np.random.rand(len(group_3_x))all_x = np.concatenate([group_1_x, group_2_x, group_3_x])all_y = np.concatenate([group_1_y, group_2_y, group_3_y])df = pd.DataFrame({"Satisfaction": all_y, "Time_spent":all_x, "Country":[0]*len(group_1_x) + [1]*len(group_2_x) + [2]*len(group_3_x)})この記事が気に入ったら、私の今後の投稿の通知を受けるために私をフォローしてください。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles






