埋め込みの視覚化

埋め込みの視覚化

高次元データを視覚化する方法は1つ以上あります。ここでは、AIの歴史にさかのぼって、これらの視覚化の進化を探求します。

私は1990年に最初のAI論文を「Midwest Artificial Intelligence and Cognitive Science Society」という小さな地元の会議に提出しました。当時、AIの分野は完全に「記号」の研究によって定義されていました。このアプローチは「Good, Old-Fashion AI」またはGOFAI（「wifi」のように「go fi」と発音）として知られていました。現在の「Deep Learning」として知られる領域で働いている私たちは、私たちが研究している内容がAIとして考慮されるべきであるかどうかを本当に議論しなければなりませんでした。

AIから除外されることは、二重の剣でした。一方で、当時定義されたAIの基本的な原則のほとんどに同意していませんでした。基本的な仮定は、「記号」と「記号処理」がすべてのAIの基礎でなければならないというものでした。そのため、AIとしてすら考慮されない領域で働いていることは幸せでした。一方で、AIに関連すると少なくとも関連付けられたアイデアを提供しない限り、人々があなたのアイデアに耳を傾けてくれるのは難しかったです。

この小さな会議は「AI」と「認知科学」に関する論文を受け付けました。私たちはそれを「記号処理」だけでなく、アイデアを広げるための招待状と見ました。そのため、最初の論文を提出し、受け入れられました！その論文は自然言語の処理におけるニューラルネットワークのアプローチを特集していました。私たちのエリアでは、このタイプのニューラルネットワークの研究を「connectionism」と呼んでいたのですが、現在ではこのタイプの研究は「Deep Learning」（DL）とラベル付けされることがあります。ただし、私の初期の研究はあまり深くありませんでした…たった3つの層だけです！現代のDLシステムは数百の層で構成されることもあります。

私の論文は会議で受け入れられ、1990年にイリノイ州カーボンデールで発表しました。後に、この会議の主催者であるジョン・ディンズモア氏から、彼がまとめている本に論文のバージョンを提出するように招待されました。一人で論文をまとめる自信がなかったため、私は私の大学院の友人2人（リサ・ミーデンとジム・マーシャル）に参加を頼みました。彼らは快く引き受けてくれ、私たちはその本の章を作成することになりました。その本のタイトルは「The Symbolic and Connectionist Paradigms: Closing the Gap」でした。私たちの論文は、この2つのAIアプローチの分割に焦点を当てていました。この分割については、今日でもまだこの分野が苦闘していると思います。

• 「キャリアのために右にスワイプ：仕事のためのTinderを作る」
• ウェブデータ駆動型製品をスケーリングする際に知っておくべきこと
• 「F1スコア：視覚的ガイド – そしてなぜそれが偏ったデータから救ってくれないのか」

私の初期の研究については後で詳しく説明します。今は、当時のフィールドが「埋め込み」の視覚化にどのように取り組んでいたかについて話したいと思います。まず、当時はこれらのベクトルを「埋め込み」とは呼んでいませんでした。ほとんどの研究では「隠れ層表現」というフレーズが使用されました。これには、問題を解決するために接続主義システムが学習した内部表現が含まれます。当時定義されていたように、3つのタイプの層がありました。「入力」（データセットを接続する場所）、「出力」（望ましい出力または「ターゲット」を配置する場所）、「隠れ」層（その他のすべての層）。隠れ層は、ネットワークの活性化が入力と出力の間を流れる場所であり、高次元の活性化はネットワークが学習した「概念」の表現です。

今日と同様に、これらの高次元ベクトルを視覚化することは、これらのシステムがどのように動作し、しばしば失敗するかを理解するための洞察を提供するのに役立つと見なされていました。私たちの本の章では、次の3つのタイプの視覚化を使用しました：

1. いわゆる「ヒントンダイアグラム」
2. クラスターダイアグラムまたはデンドログラム
3. 2D空間への射影

最初の方法は、1991年にHintonとShalliceによって新たに作成されたアイデアでした（それは今日私たちが知っているGeoffrey Hintonです。将来の記事で詳しく説明します）。このダイアグラムは、限られた有用性を持つシンプルなアイデアです。基本的なアイデアは、活性化、重み、または任意の数値データをボックスで表現することです：白いボックス（通常は正の数を表す）、黒いボックス（通常は負の数を表す）。さらに、ボックスのサイズは、値がシミュレートされたニューロンの最大値と最小値に対する値の大きさを表します。

以下は、私たちの論文からの表現です。ネットワークの隠れ層における単語の表現としての平均的な「埋め込み」を示しています：

Hintonダイアグラムはデータ内のパターンを視覚化するのに役立ちます。しかし、表現間の関係を理解するのにはあまり役立たず、次元の数が大きくなるとさらに役立ちません。現代の埋め込みは、数千の次元を持つことがあります。

これらの問題を解決するために、私たちは第2の方法であるクラスターダイアグラムまたはデンドログラムに注目します。これらは、任意の2つのパターン間の距離（どのように定義されているかによる）を階層的な木として示すダイアグラムです。ここでは、ユークリッド距離を使用した私たちの論文の例を示します:

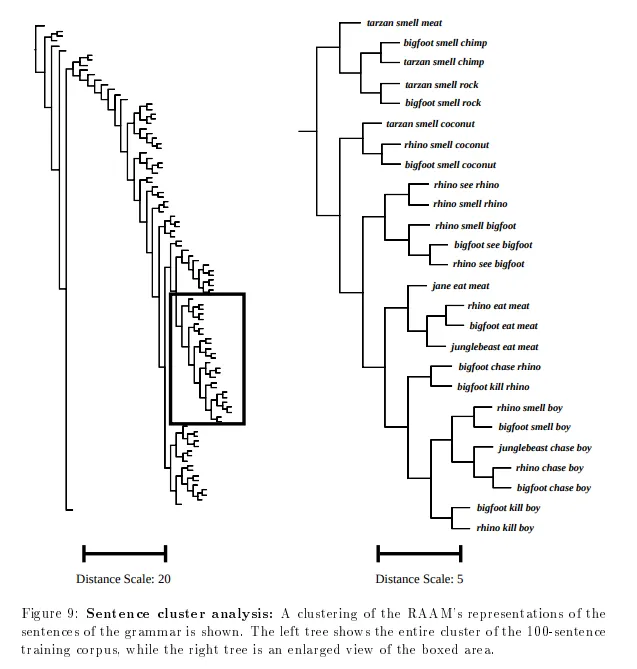
これはHintonダイアグラムに表示される情報と同じ種類ですが、はるかに有用な形式です。ここでは、個々のパターンや全体的なパターンの内部関係が見えます。垂直の並べ替えは無関係です。枝の位置がダイアグラムの意味的な側面です。

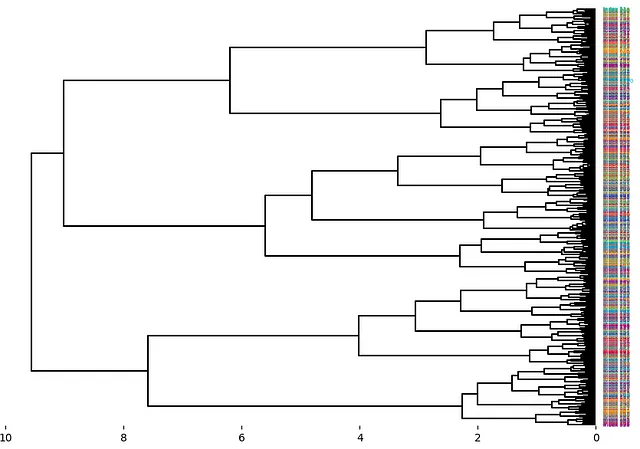
上記のデンドログラムでは、プログラムによって計算されたツリークラスターに基づいて全体のイメージを手作業で作成しました。現在では、そのようなツリーやイメージを自動的に構築するための方法があります。ただし、パターンの数が数十以上の場合、ダイアグラムは意味を持つのが難しくなることがあります。ここでは、matplotlibを使用して作成された例を示します。APIについては、こちらのmatplotlib dendogramをご覧ください。

最後に、最も一般的に使用されている方法であるプロジェクション方法に移ります。この方法は、埋め込みの次元を人間が理解しやすい数値（例：2次元または3次元）に削減するためのアルゴリズムを使用し、散布図としてプロットします。

1990年当時、高次元データをより小さな次元のセットに投影する主な方法は、主成分分析（PCA）でした。次元削減は活発な研究領域であり、新しい方法がまだ開発中です。

現在、最も使用されている次元削減のアルゴリズムはおそらく次のとおりです:

1. PCA
2. t-SNE
3. UMAP

どれが最適かは、データの詳細と次元削減の目標によります。

PCAはおそらく全体的に最も優れた方法です。なぜなら、決定論的であり、高次元空間から削減空間へのマッピングを作成できるからです。これは、1つのデータセットでトレーニングを行い、その後テストデータセットが学習された空間にどのように投影されるかを調べるのに役立ちます。ただし、PCAはスケーリングされていないデータの影響を受ける場合があり、構造的なパターンに対してあまり洞察を提供しない「点の集まり」となることがあります。

t-SNEは、t-distributed Stochastic Neighbor Embeddingの略で、RoweisとHinton（はい、あのHintonです）によって2002年に作成されました。これは学習されたプロジェクションであり、スケーリングされていないデータを利用することができます。ただし、t-SNEの欠点の1つは、マッピングを作成しないことで、クラスタリングを見つけるための学習方法そのものです。つまり、Projection.fit()やProjection.transform()のような他のアルゴリズムとは異なり、t-SNEはフィットのみを実行できます。（openTSNEなどの実装では、変換マッピングが提供されるものもありますが、openTSNEは他のアルゴリズムとは非常に異なり、遅く、他の形式よりもサポートが少ないようです。）

最後に、Uniform Manifold Approximation and Projection（UMAP）と呼ばれる方法があります。これは、McInnesとHealyによって2018年に作成されました。多くの高次元空間にとって、これは最適な妥協点かもしれません。計算コストが比較的低く、同時に削減された次元で重要な表現構造を保存できます。

ここでは、sklearnで利用可能なスケーリングされていない乳がんデータに次元削減アルゴリズムを適用した例を示します:

自分自身で次元削減アルゴリズムをテストして、使用ケースに最適なものを見つけ、上記のような画像をKangas DataGridを使用して作成することができます。

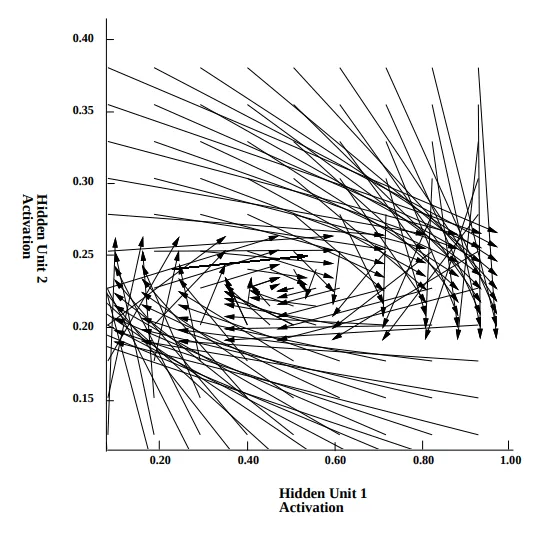
前述の通り、次元削減はまだ活発な研究分野です。ディープラーニングネットワーク内の情報の流れを視覚化するなど、この分野では今後も改善が期待されます。以下は、私たちの書籍の章で示されたモデルの表現空間におけるアクティベーションの流れを示す最後の例です：

人工知能、機械学習、データサイエンスのアイデアの発信元に興味がありますか？ぜひ拍手と購読をお考えください。ご興味のある内容をお知らせください！

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!