「圧縮が必要ですか？」

圧縮が必要ですか？

圧縮ベースのトピック分類のより効率的な実装

最近公開された「Low-Resource」Text Classification: A Parameter-Free Classification Method with Compressors [1] というタイトルの論文が、最近注目を集めています。彼らの主な発見は、2つのテキストドキュメントがより小さなファイルサイズに圧縮できる場合、それらはより類似しているという単純なアイデアを用いて、BERTのような大規模言語モデルを上回ることができる場合があるということです（ただし、彼らの結果の妥当性については議論があり、このブログ記事と著者の回答を含むこの議論を参照してください）。

彼らの手法の主なアイデアは、Bennetらによって定義された2つのドキュメント間の「情報距離」が、テキスト分類中に使用する良い距離尺度であるということです。情報距離自体は計算できないため、彼らはNormalized Compression Distance (NCD) [3] を使用してそれを近似します。NCDはgzipなどの「実際のデータ圧縮器」を使用して情報距離を推定するものであり、より良い圧縮器（つまり、圧縮率がより良い圧縮器）は真の情報距離のより良い推定を可能にします。

したがって、より良い圧縮器が分類で優れたパフォーマンスを発揮することが自然な期待です。しかし、彼らはこれを実験的に検証することはできません。論文で最も優れた圧縮器とされているbz2は、正確性の点でgzipよりも劣っています。彼らは次のように説明しています。「bz2が使用するBurrows-Wheelerアルゴリズムは、圧縮中に文字の順序の情報を破棄するため、圧縮だけでは彼らの結果を説明できない、文字の順序にも何か関連があるということです」[1, p.6817]。

これにより、私は疑問に思いました。彼らの結果のどれくらいが圧縮によるものであり、どれくらいが2つのドキュメント間の文字列の比較によるものなのかを調査してみました。

• 「CLAMPに会ってください：推論時に新しい実験に適応できる分子活性予測のための新しいAIツール」
• 最終的なDXAネーション
• 「プリズマーに会いましょう：専門家のアンサンブルを持つオープンソースのビジョン-言語モデル」

この問いに答えるために、私は彼らの結果を2つの代替手法と比較しています：（1）再現する文字列の置換のみに依存する単純な圧縮器、および（2）クエリドキュメントと特定のトピックに属するすべてのドキュメントとの間で明示的に部分文字列の一致を行うアルゴリズム。

最初の削除実験：LZ4はうまくいくか？圧縮アルゴリズムgzipは、DEFLATEに基づいており、DEFLATEはLZ77とハフマン符号化を使用してデータを圧縮します。これら2つのアルゴリズムについて詳しく見て、私たちの利用事例に適用した場合にそれらがどのような意味を持つのか考えてみましょう。

圧縮中、LZ77は以前に見たデータのスライディングウィンドウを使用します。文字列が繰り返される場合、文字列自体ではなく、最初に出現する文字列への参照が保存されます。したがって、2つの連結ドキュメントの長さを距離尺度として取ると、ドキュメント同士がスライディングウィンドウのサイズ（通常は32KB）以内で重複する部分文字列が多いほど、ドキュメント同士はより近くなります。

Huffman符号化は、結果のテキストをさらに圧縮します：各文字に8ビットを使用する代わりに、よく出現する文字は少ないビットで表現し、まれに出現する文字は多くのビットで表現します。連結ドキュメントにハフマン符号化を適用すると、2つのドキュメントは、文字の出現頻度が似ている場合に圧縮後に小さくなります。

トピック分類においては、一致する部分文字列が非常に重要であることが予想されます。そのため、圧縮に関してはLZ4のアルゴリズム [4] を使用して圧縮を行った場合のパフォーマンスを調査します（基本的にはLZ77ですが、Pythonで利用可能な高速な実装です）。LZ4はgzipよりも圧縮率がはるかに低いため、彼らの説明が正しければ、LZ4のパフォーマンスはgzipよりも劣るはずです。ただし、もし主要な要素が部分文字列の一致である場合、LZ4はgzipと同じくらい優れたパフォーマンスを発揮するはずです。

より明示的なアルゴリズムさらに進んで、明示的に部分文字列の一致を行う単純なアルゴリズムを実装します：ドキュメントを最も類似した部分文字列（ここでは文字レベルのn-gram）を持つトピックに割り当てます。アルゴリズムは次のように機能します：

テキストエンコーディング：1. テキスト内のすべての文字n-gram (5 ≤ n ≤ 50) を抽出します。2. 抽出したn-gramに対して、Pythonで `hash(n_gram) % int(10e8)` を使用して8桁のハッシュコードを計算します（異なる要素の数を制御したいため）。3. これを集合で追跡します（そのため、特定のコードが何回出現するかの情報は失われます）。

トレーニング：1. 与えられたトピックのすべてのテキストに対してハッシュコードのセットを計算します。2. トピック内で発生するハッシュコードのセットを取得するために、セットの和集合を計算します。

推論：1. クエリのテキストに対してハッシュ化されたn-gramのセットを計算します。2. トレーニング中に出会ったすべてのトピックについて、トピックのセットとクエリのセットの共通部分のサイズを計算します。3. 最も共通部分が大きいトピックにクエリのテキストを割り当てます。

実験と結果私は、彼らの論文で説明されている通り、100ショット設定でgzip、lz4、およびハッシュ化されたn-gramアルゴリズムの結果を5回の実行で比較します。 3つのメソッドすべてについて、報告された結果を再現するために彼らの実験のセットアップを使用します（再び、潜在的に膨張した精度の尺度を残します）。 コードはgithubで見つけることができます。

次の表には、torchtextの3つのデータセット（AG_NEWS [5]、DBpedia [6]、およびYahooAnswers [5]）のパフォーマンスが表示されています：

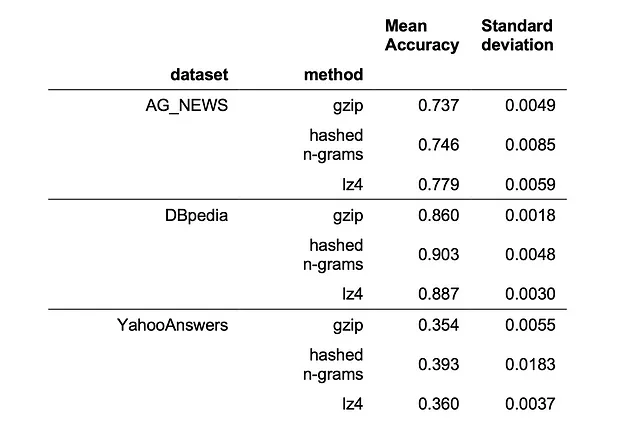
私たちは、lz4とハッシュ化されたn-gramがすべての3つのデータセットでgzipを上回り、ハッシュ化されたn-gramアルゴリズムが3つのデータのうち2つで最も優れていることがわかります。ただし、それはまだBERTには敵わないです。BERTは、AG_NEWSでは0.82、そしてDBpediaではほぼ1の性能を持っていると彼らの論文によると、100ショット設定で。

これらの結果には重要な実用的な意味があります。私たちの実験では、lz4ベースのアルゴリズムは、gzipベースのアルゴリズムよりも約10倍高速に実行されます。さらに重要なことは、ハッシュ化されたn-gramアルゴリズムは推論時の計算量を改善することです。クエリドキュメントをテキストコーパスの他のすべてのドキュメントと比較する必要がある代わりに、トピックセットとの比較を行うだけです。

これから学ぶことは何ですか？私の結果は、gzipの印象的な報告されたパフォーマンスの原動力は、彼らのメソッドが暗黙的にドキュメント間の文字レベルのn-gramを比較していることに帰因できると示唆しています。この結果、lz4などの高速な圧縮器を使用することができ、パフォーマンスに影響を与えることはありません。さらに重要なことは、データセットサイズに関して定数の計算量を持つようにアルゴリズムを再書きすることができるため、この方法はビッグデータセットでの実用的な使用に一歩近づくということです。実際に使用する場合は、私は提案されたアルゴリズムのscikit-learn APIに従った実装を開始しました。

残る1つの質問は、単語間も比較するTF-IDFアプローチよりもなぜこれが優れているのかということです。

文字レベルのn-gramを考慮することで、テキストを個々の単語に分割するよりも、一部のタスクにおいてより良い結果を得ることができるかもしれません。しかし、おそらくもっと重要なのは、ここでのメソッドは、出現回数に関係なくすべてのn-gramに等しい重みを与えるということです。これは、いわゆるロングテール（つまり、稀な）情報に多大な重要性を与えることを意味し、それはトピック検出などのテキストタスクにおいて明らかに重要です。注意すべきは、トランスフォーマーネットワークがこのようなロングテール情報をモデリングするのにあまり適していないということです（証拠については、例えば[5]を参照）。そのため、これらの非常にシンプルなアプローチは、百万パラメータモデルに対する非常に興味深いベンチマークとなります。

参考文献[1] Z. Jiang, M. Yang, M. Tsirlin, R. Tang, Y. Dai, J. Lin. “Low-Resource” Text Classification: A Parameter-Free Classification Method with Compressors (2023), ACL 2023[2] C. H. Bennett, P. Gács, M. Li, P. MB Vitányi, and W. H. Zurek, Information distance (1998), IEEE Transactions on information theory[3] M. Li, X. Chen, X. Li, B. Ma, and P. Vitányi, The similarity metric (2004), IEEE transactions on Information Theory[4] N. Kandpal, H. Deng, A. Roberts, E. Wallace, C. Raffel, Large Language Models Struggle to Learn Long-Tail Knowledge (2022), arxiv.org/abs/2211.08411

Joel NiklausさんとMarcel Gygliさんに感謝します。私たちの議論とフィードバックに。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!