『周期的な時間特徴のエンコード方法』
周期的な時間特徴のエンコード方法
ディープラーニングや他の予測モデルのための日付、曜日、および時間の注意深い処理。

多くの予測タスクでは、モデルの入力として時間情報が必要です。小売会社のレモネードの売上を予測する回帰モデルを考えてみましょう(コンテキスト豊かな特徴についての私の記事からの例を覚えているかもしれません)。暑い夏にはさわやかな飲み物の需要が明らかに高くなり、7月/8月にピークを迎える周期的な売上曲線が生じます(ここではヨーロッパの場所を考えてみてください)。
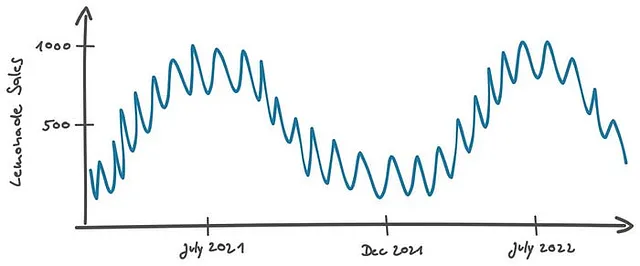
この場合、年の中での時間は明らかに有益な季節情報であり、モデルに入力する必要があります。しかし、どのようにすれば良いのでしょうか?日付は難しいです。月によって日数が変わります(2月の場合はさらに年によっても異なります)し、さまざまな形式が存在します:
2023年1月13日
- 「Googleは、Raspberry Pi向けにMediaPipeを導入し、デバイス内の機械学習のための使いやすいPython SDKを提供します」
- 人工知能の台頭に備えるために、高校生をどのようにサポートできるか
- ロボットスキル合成のための言語から報酬への変換
13.01.2023
2023/03/13
まず、年を省略できます。季節効果を考慮するために、日と月だけが必要です。非常にシンプルな(そして考慮が足りない)アプローチでは、月を1つの数値として、日を別の数値として入力するだけです。
なぜそれが悪い考えなのでしょうか?モデルはキリスト教のグレゴリオ暦の働き方(月あたり約30日、年あたり12ヶ月、閏年など)を学習する必要があります。十分なトレーニングデータがあれば、ディープラーニングモデルは私たちのカレンダーを「理解」することができるはずです。「理解」とは、この場合、モデルが月と日の入力から年の相対的な時間位置を推測できることを意味します。しかし、モデルの学習をできるだけ簡単にするために、私たちはこの仕事を引き受けるべきです(少なくとも私たちはすでにカレンダーの働き方を知っています)。Pythonのdatetimeライブラリを利用して、年の相対的な時間をかなりシンプルなロジックで計算します:import datetime as
from datetime import datetimeimport calendaryear = 2023month = 12day = 30passed_days = (datetime(year, month, day) - datetime(year, 1, 1)).days + 1nr_of_days_per_year= 366 if calendar.isleap(year) else 365position_within_year = passed_days / nr_of_days_per_year1月1日に近い値から12月31日に近い値までの範囲を持つposition_within_yearという結果の特徴は、(厄介な)グレゴリオ暦よりもモデルにより簡単に解釈できます。
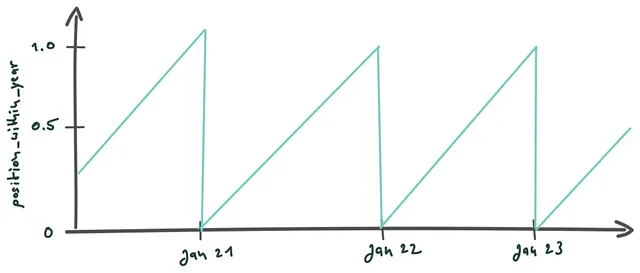
しかし、まだ理想的ではありません。position_within_year特徴は、年ごとに1.0から0.0への急なジャンプという「のこぎり歯状」のパターンを示しています。この急激な不連続性は、効果的な学習に問題を引き起こす可能性があります。12月31日と1月1日は非常に似た日付です。直接の隣人であり、多くの共通点(例えば、似たような天候条件)を持ち、おそらくレモネードの売上の類似の潜在力を持っています。しかし、position_within_year特徴は、12月31日と1月1日に対してこの類似性を反映しておらず、実際には可能な限り異なる値です。
理想的には、互いに近接している時点は似たような時間値を持つべきです。年の周期性を表す特徴を設計する必要があります。つまり、12月31日には1月1日に戻る位置に到達するのが合理的です。ですので、当然のことですが、年の内部位置を円の位置としてモデル化することは意味があります。これを実現するために、position_within_yearを単位円のx座標とy座標に変換します。
これにはサインとコサインの関数を使用します:
sin(α) = x
cos(α) = y
αは円に適用される角度です。単位円が1年を表す場合、αは既に経過した年の中の時間を表します。
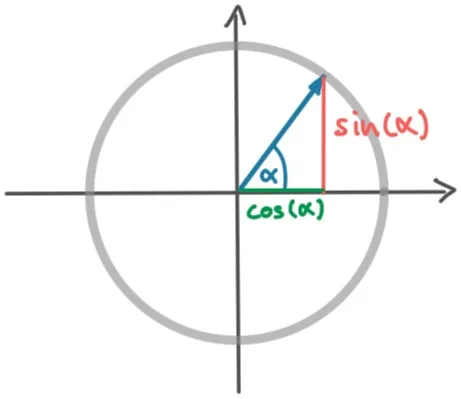
αは、position_within_yearと同等であるが、スケールが異なる点が異なります(α: 0.0–2π¹、position_within_year: 0.0-1.0)。
position_within_yearをαにスケーリングし、正弦と余弦を計算することで、「鋸の歯」のパターンを円形の表現に変換します。
import math# scale to 2pi (360 degrees)alpha = position_within_year * math.pi * 2year_circle_x = math.sin(alpha)year_circle_y = math.cos(alpha)# scale between 0 and 1 (original unit circle positions are between -1 and 1)year_circle_x = (year_circle_x + 1) / 2year_circle_y = (year_circle_y + 1) / 2time_feature = (year_circle_x, year_circle_y) # 美しいですね ;)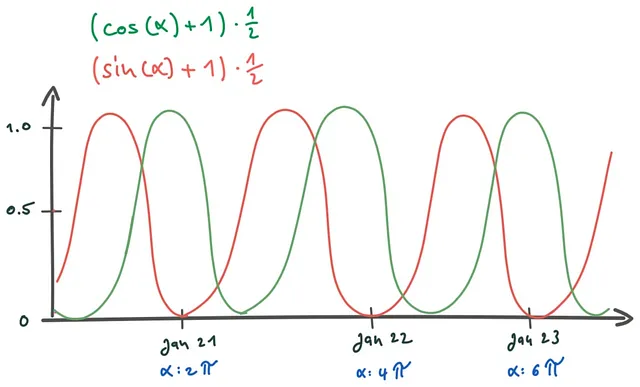
結果として得られるtime_featureは、0から1までのスケールで表される2要素のベクトルであり、予測モデルが簡単に処理できます。わずか数行のコードで、モデルにとって不必要な学習作業を大幅に削減しました。
単位円モデルは、月の日、週の日、一日の時間、一時間の分など、任意の周期的な時間情報に適用することができます。この概念は、時間領域外の循環的な特徴にも拡張することができます:
- 物流/公共交通:市内を往復するバスの相対的な位置
- 生物学:細胞周期内の細胞の状態。
- 他の使用例はありますか?コメントで書いてください!
さらなる情報/接続ポイント
- Pierre-Luis Bescond氏による同じトピックに関する素晴らしい実践的な記事。
- ディープラーニングモデルの特徴エンジニアリングについてもっと学びたいですか?コンテキスト豊かなデータについての私の記事をチェックしてください。
- 質問がありますか?AI、データサイエンス、データエンジニアリング、Python開発のフリーランスエキスパートが必要ですか?私のウェブサイトにアクセスして、メッセージを送ってください。
[1] ここでは角度はラジアンで与えられます。ラジアンの0は0°に相当し、ラジアンの2πは360°に相当します。
すべての図は著者によって作成されました。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles