「勾配降下法アルゴリズムとその直感的な考え方」

勾配降下法アルゴリズムの直感的な考え方

勾配降下法の技術的な説明とアルゴリズムの動作を補完するグラフィカルな表現

1. キーとなる定義の紹介

最適化手法の中で、そして一次アルゴリズムのタイプについて、勾配降下法というものを聞いたことがあるでしょう。勾配降下法は一次最適化のタイプであり、一次導関数である勾配を必要とします。最適化によって、勾配降下法は「実際の」出力とモデルの予測出力との差を最小化することを目指します。この差は目的関数、すなわちコスト関数によって測定されます。勾配は、曲線または直線の点での関数が描く線の方向として定義されます。反復的に、勾配降下法は異なる点でのコスト関数を微分し、これらの点での方向の変化の度合いを導き出し、最も急な降下、つまり局所最小値に向かってステップを踏みます。その名前が示すように、勾配は最小値を探索するための方向として使用されます。最適化されるコスト関数のパラメータの値が最小化される場所、すなわち最も低い値が得られる場所です。

勾配降下法は、機械学習モデルやディープラーニングモデル（後者はニューラルネットワークのアーキテクチャタイプに基づいています）のトレーニングにおいて主に使用されます。線形回帰やロジスティック回帰からニューラルネットワークまで、勾配降下法は関数の最適なパラメータ値を計算することを目指します。最も単純な形式では、勾配降下法は以下の線形回帰の誤差項を最小化することを目指し、独立変数のパラメータの最適な値を導出します。つまり、

y = β0 + β1 * X1 + … βk * Xk + Ɛ

ここで、

• ハギングフェイスがIDEFICSを導入：視覚言語モデルを活用した先駆的なオープンマルチモーダル対話AI
• 画像認識におけるディープラーニング：技術と課題
• 『見て学ぶ小さなロボット：このAIアプローチは、人間のビデオデモンストレーションを使用して、ロボットに汎用的な操作方法を教える』

yは従属変数

kは独立変数の数

Xは独立変数

βはパラメータ

Ɛは誤差項の成分

より複雑な形式では、勾配降下法は主にディープラーニングモデルのトレーニング時に最適化として定義されます。ディープラーニングは、学習と持続的な改善を目指す相互接続されたネットワークに基づいています。すなわち、ニューラルネットワークです。人間の脳に触発されたニューラルネットワークは、ノードとして知られる人工ニューロンによって表される非常に複雑なネットワークです。トップレベルでは、ノードは前の層のノードからのデータを処理し、次の層のノードに渡します。ニューラルネットワークでは、重みと呼ばれるパラメータがノード間のリンクです。これらは入力/特徴と隠れ層の間のリンクであり、最終的な出力を予測するための特定の特徴の重要性を表します。単一の重みの最適な値を見つけるためには、多くの重みの値に依存します。そして、この最適化は一度に多くの重みに対して行われます。ディープニューラルネットワークでは、これらの重みが非常に多くなる場合があります。勾配降下法は、このような多数の計算において非常に効率的に実行されることが分かっています。これらの計算は、ニューラルネットワークの3つの主要な層に基づいています：1）入力層、2）隠れ層、および3）出力層。

ディープラーニングや関数のパラメータの値を推定する方法といった深層学習や勾配降下法と最小二乗法（OLS）との違いについて、詳細かつ拡張した論文が数多く存在します（例えば、線形回帰の場合）。この論文ではその焦点ではないため、読者はさらに調査を行い、これらの方法について理解を深めることが求められます。

2. 微積分の時間です！

勾配降下法を理解するためには、微分可能な関数の定義について詳しく説明する必要があります。関数ƒ(x)が微分可能であるとは、その関数が導かれる曲線の任意の点で導関数が定義できることを意味します。つまり、関数ƒ(x)の定義域のすべての点に対してです。ここで、この定義を補強する2つの概念があります：一次導関数と二次導関数です。一次導関数の公式は次のように定義されます：

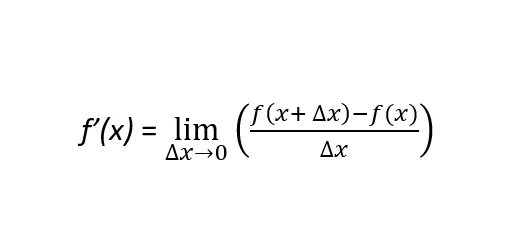
厳密に言えば、関数の一次導関数はƒ’(x)またはdf(x)/dxと表示され、xの特定の値における関数ƒ(x)の傾きを表します。傾きが正の場合（負の場合）、関数が増加している（減少している）こと、およびその程度を示します。正の傾きは、xの値が増加すると関数ƒ(x)も増加することを示します。一方、負の傾きは、xの値が増加するとƒ(x)が減少することを示します。2次導関数は、関数ƒ(x)の導関数の導関数です。ƒ’’(x)またはd2f(x)/dx2と表示され、2次導関数は関数ƒ(x)の形状を示します。つまり、その関数が凸または凹であるかどうかです。数学的に言えば（これは重要です！）、2次導関数は相対的な最大値と相対的な最小値を区別します。

ここで、

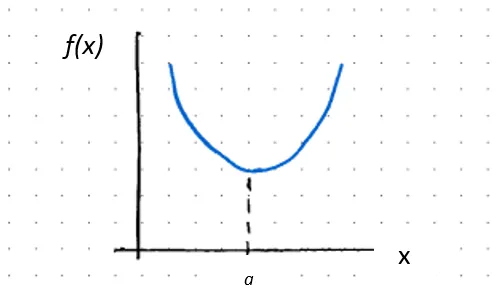
ƒ’’(x) > 0の場合、ƒ(x)はx = aで凸である

ƒ’(a) = 0の場合、aは臨界点であり、相対的な最小値です

ここで、

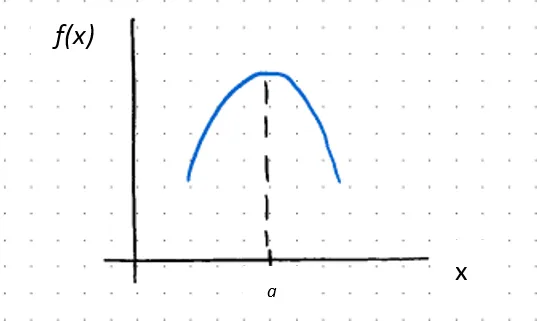
ƒ’’(x) < 0の場合、ƒ(x)はx = aで凹である

ƒ’(a) = 0の場合、aは臨界点であり、相対的な最大値です

または、2次導関数がゼロに等しい場合、次のいずれかが成り立ちます。1）関数ƒ(x)が転換点である場合、つまり凹から凸または凸から凹に変わる場合、または2）その点の関数が未定義である場合（すなわち連続でない場合）。前者の場合：

ƒ’’(x) = 0の場合、ƒ(x)はx = 2で転換点にあります

上記は、単一の独立変数（つまり単変量関数、y = ƒ(x)）を持つ関数に焦点を当てています。現実世界では、複数の独立変数に影響を受ける多変数関数を研究しモデリングすることになります。つまり、y = ƒ(x, z)のように2つ以上の独立変数があります。独立変数xの変化が従属変数yに与える影響を測定するために、xに関する関数の偏微分が行われます。したがって、偏微分はそれぞれの入力の変化によるコスト関数の変化率を計算します。勾配降下法は、これらのコスト関数の変化を反復的に計算し、各ステップでその関数のパラメータの値を更新し、パラメータの値が最適化され、つまりコスト関数が最小化されるまで繰り返します。

3. 勾配降下法の動作

傾きの絶対値が大きいほど、より遠くに進むことができます。また、最急降下、つまり局所最小値に向かってステップを続けることもできます。最低/最小点に近づくにつれて、傾きは減少するため、フラットな表面に到達するまでより小さなステップを取ることができます。このフラットな表面では、傾きがゼロ（0）に等しい（ƒ’(x) = 0）ため、曲線の最小値があり、関数のパラメータの最適な値が導かれます。

したがって、関数が厳密に凸（凹）である場合、臨界点は1つだけです。次に、複数の局所最小値が存在する場合もあります。この場合、探索は関数が達成できる最も低い値を求めるためのものです。これがグローバル最小値として知られています。

次に、次の2つの重要な質問が浮かび上がります：

1) どの方向に進むべきか？

2) ステップの大きさはどれくらいであるべきか？

ここまでの話を振り返ってみましょう。勾配降下法は、モデルのトレーニングフェーズ中に、関数のパラメータの値を反復的に調整し、最急降下と定義される局所最小値に向かって各ステップで関数の各入力に対する偏微分を取ることによって最適化するアルゴリズムです。導関数が正の場合、関数は増加しています。したがって、逆の方向にステップを進める必要があります。勾配はステップを進めるべき方向を示します。勾配が大きい場合、つまり大きな傾きの絶対値が大きい場合、局所最小値に向かってより大きなステップを進める必要があります。実際、勾配降下法は、上記のグラフの青い矢印に示されるように、各反復で局所最小値の方向に対してますます小さなステップを取ります。

ステップの大きさは学習率と関連しています。これはアルゴリズムが最急降下に向かって学習/移動する速度です。最も高い勾配では、スロープの絶対値が大きいほど、アルゴリズムは最も速く学習します。局所最小値に近づくにつれて、ステップは小さくなります。したがって、学習率の値は、イテレーションごとにコスト関数が減少するように異なる値を試した後に設定されます。大きすぎる場合、局所最小値を見逃す可能性があります。小さな学習率は、重みの更新が小さくなり、モデルが大幅に改善しない可能性があります。小さすぎると収束するまで時間がかかります。収束は、コスト関数がもはや減少しないときに達成されます。したがって、コスト関数はアルゴリズムのパフォーマンスを示す指標です。多変数関数の世界では、次のように表されます：

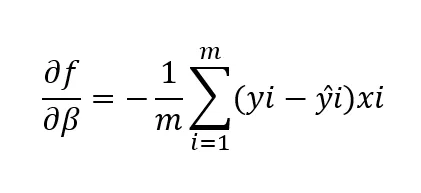
ここで、

df/dβは、パラメータβに関するコスト関数の偏微分です

mはデータポイントの数です

yiはi番目のデータポイントの実際の依存変数/ターゲット変数の値です

ŷiはi番目のデータポイントの依存変数/ターゲット変数のモデルによる予測値です

xiはデータポイントに関連するi番目の入力を表します。

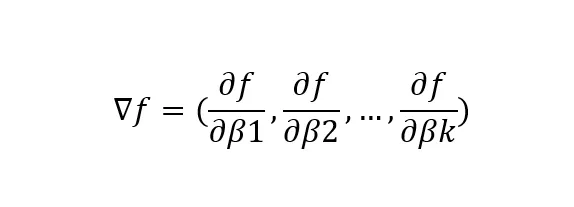
ここで、

▽fは関数f(x)のパラメータβに関する勾配ベクトルを表します

df/dβkは関数f(x)のk番目のパラメータβに関する偏微分を表します

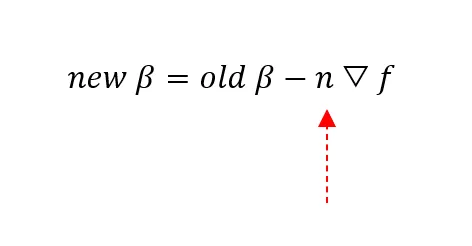
ここで、

New βはi番目のパラメータβの現在の値を表します

Old βはi番目のパラメータβの更新された値を表します

nは学習率：取るステップの長さです！

▽fは、関数f(x)のパラメータβの変化に対して最小化するための最急降下の方向を指す勾配ベクトルです

4. 勾配降下法の制限事項

勾配降下法の制限事項の1つは、関数がドメインのすべての点で微分可能である必要があるという前述の基準に関連しています。これが満たされない場合、アルゴリズムは定義されていない点（つまり、非連続な点）を見つけてしまい、失敗します。

別の制限事項は、最急降下に向かって取るステップの大きさ、つまり学習率（n）に関連しています。大きすぎる場合、局所最小値を見逃す可能性が高く、収束さえしない場合もあります。小さすぎる場合、収束するまでに時間がかかります。入力の数が多い場合、これはさらに問題が生じます。

最後に、勾配降下法は必ずしもグローバルミニマムを見つけることができません。アルゴリズムはローカルミニマムとグローバルミニマムの違いを区別することができません。ローカルミニマムを探求するにつれて収束すると停止します。ローカルミニマムはアルゴリズムを自身の谷に閉じ込め、ステップが十分に大きくなることを妨げます。

5. 結論

まとめると、勾配降下法は以下のような特徴を持っています：

1) 反復的な一次最適化アルゴリズムです。

2) 各反復ごとに、微分可能な関数のパラメータが更新され、コスト関数が最小化されます。

3) したがって、収束はローカルミニマムで達成されます。

勾配降下法の制約に基づいて、より高度な勾配降下法の手法や最適化の他の手法（例：二次の手法）を探求する動機があります。ただし、これは本記事の範囲外ですので、次の記事のトピックとして取り上げます😊

読んでいただきありがとうございました！

トピックの知識を高めるコメントをお願いします！

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!