分岐と限定法 -アルゴリズムをスクラッチからコーディングする前の導入
分岐と限定法 -アルゴリズムの導入
整数問題への導入とその解決方法の一つ
導入
整数計画(IP)は、決定変数が整数値に制約される線形計画(LP)の特殊な場合です。つまり、2.5や4.2などの値はこれらの問題の解としてはあり得ません。
この要件はLPへの追加の制約として扱われ、最適解を見つけるプロセスをより困難にします。
現実の生活では、私たちが抱える多くの問題がIPの形を取ります。たとえば、資本予算と割り当てでは、どの投資を行うかを決定するために、決定変数はバイナリであり、値は0と1のみを取ります。不動産のサイト選択問題、車両の経路、スケジューラの問題もおそらくこれに該当します。
この記事では、整数問題(IP)を解決するために使用されるアルゴリズムの一つである分枝限定法アルゴリズムを探っていきます。
私はCornuejolsとTütüncüの書籍「Optimization Methods in Finance」の例を借りて説明しますが、自分なりの直感的な説明ともちろん、そのようなアルゴリズムのPython実装も追加します。
分枝限定法アルゴリズム
分枝限定法アルゴリズムは、IPを解決するための最も一般的な手法の一つです。このアルゴリズムは、元の問題をより小さな副問題に分割することで(分枝)、その過程でいくつかの解を試し、現在の解よりも良い結果にならない場合にこれらの解の一部を除外することができます(枝刈り/剪定)。
これは理解するのが難しいですが、例を使うとわかりやすくなります。
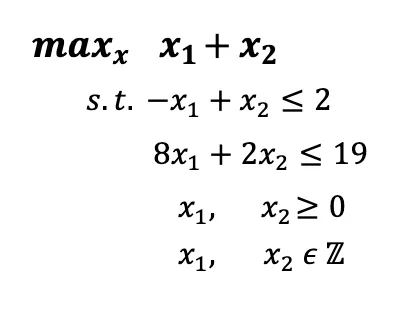
上記の問題0は私たちの元の整数問題です。最後の行に追加の制約がある単純な線形計画問題です。
ステップ1 – 線形計画緩和
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles






