共和分対スパリアス相関：正確な分析のための違いを理解する

共和分対スパリアス相関の理解

時系列における相関と因果関係の違い

背景

時系列分析では、ある系列が他の系列に影響を与えるかどうかを理解することが価値があります。例えば、商品取引業者にとって、商品Aの増加が商品Bの増加につながるかどうかを知ることは役に立ちます。もともと、この関係は線形回帰を用いて測定されていましたが、1980年代にクライブ・グレンジャーとポール・ニューボールドは、特に非定常な時系列に対してこの手法が誤った結果をもたらすことを示しました。その結果、彼らは共和分という概念を考案し、グレンジャーはノーベル賞を受賞しました。この記事では、共和分の必要性と応用、そしてデータサイエンティストが理解すべき重要な概念である理由について議論したいと思います。

見かけの相関

概要

共和分について話し合う前に、その必要性について話し合いましょう。歴史的に、統計学者や経済学者は異なる時系列間の関係を判断するために線形回帰を使用していました。しかし、グレンジャーとニューボールドはこの手法が誤っており、見かけの相関というものにつながることを示しました。

見かけの相関とは、二つの時系列が相関して見えるが、実際には因果関係がない状態を指します。これは典型的な「相関は因果関係を意味しない」という言葉です。統計的なテストでも、因果関係があると判断されることがありますので、危険です。

例

見かけの関係の例を以下のプロットで示します：

• 「ChatGPTの王座陥落：クロードが新しいAIリーダーとなった経緯」
• 「ジャスティン・マクギル、Content at Scaleの創設者兼CEO – インタビューシリーズ」
• Pythonを使用してDLISファイルの内容を探索する

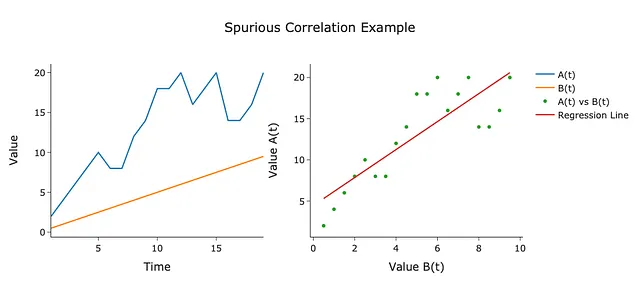
ここでは、時間の関数としてプロットされた二つの時系列A(t)とB(t)があります（左）また、互いにプロットされたものもあります（右）。右側のプロットからわかるように、回帰直線によっていくつかの相関が見られます。しかし、左側のプロットを見ると、B(t)が一貫して増加している一方で、A(t)は乱れて変動しています。さらに、二つの時系列間の平均距離も増加しています…

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!