「不確定性原理は時間系列解析をどのように制限するのか？」

不確定性原理と時間系列解析の制限は？

なぜ時間系列から正確な時間と周波数情報を相互に抽出できないのか、およびウェーブレット解析がこの制限に対処する方法

1. はじめに

フーリエ変換、不確定性原理、および時間系列解析の関係性は、同時的な時間と周波数情報の抽出を形成する魅力的な相互作用を明らかにします。この関係を理解するためには、まずフーリエ変換（FT）と不確定性原理がどのような結果として現れるのかを簡単に理解することが重要です。その後、この制限に対して有望なツールであるウェーブレット変換（WT）を探求し、十分な明瞭さで特定の周波数の時間的な発生を明らかにします。

1.1 フーリエ変換

フーリエ変換（FT）は、関数の時間領域と周波数領域の間の数学的な橋渡しとして機能します。FTは次のように記述できます：

この積分の詳細には触れませんが、重要な部分は、FTが関数f(x)を周波数空間の別の関数g(ω)に変換することです。 この情報を後で活用します。 （FTの理解を深めるためには、3Blue1Browの動画を強くお勧めします。）

• 「ジオスペーシャルデータエンジニアリング：空間インデックス」
• 「今日必要なマーケティング分析とデータサイエンスのプロが持つべき5つのスキル」
• Panderaを使用したPySparkアプリケーションのデータ検証

1.2 フーリエ変換の結果としての不確定性原理

1927年、物理学者ヴェルナー・ハイゼンベルクは、量子力学に関するおそらく最も有名な概念の1つである不確定性原理を導入しました[1]。 この原理は基本的にはフーリエ変換に関する定理です。2つの関数が互いにフーリエ変換である場合、不確定性原理が発揮されます。

物理学の複雑な側面を一時的に横に置いて、本質だけを考えてみましょう：位置xと運動量pの不確実性の積は制約されます。 この制限により、これらの量を無限の精度で測定することはできません（興味がある場合は、この動画をご覧ください）。

これは、位置と運動量が互いにフーリエ変換であるためです！ 時系列解析の場合、位置xと運動量pのアナログは、時間tと周波数ωの空間における時系列です。

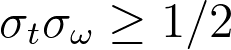
2. 時系列データでのフーリエ変換による周波数の顕在化

フーリエ変換の非常に重要な応用の1つは、時系列データの解析です。時系列内の固有の周波数を見つける必要がある場合を考えてみましょう。たとえば、人々が与えられたコンテンツを再視聴する頻度を識別することを考えてみましょう。したがって、我々は時系列f(t)（時間系列）を周波数の関数g(ω)に変換するために、FTを使用したいのです。

2.1 例

例として、Mauna Loa週間大気CO2データセット[2]を使用しましょう。

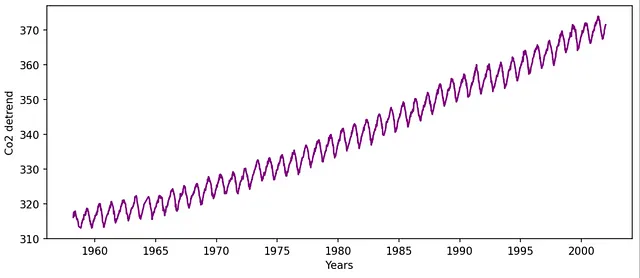
偽の低周波成分を除去するために線形傾向を除去します：

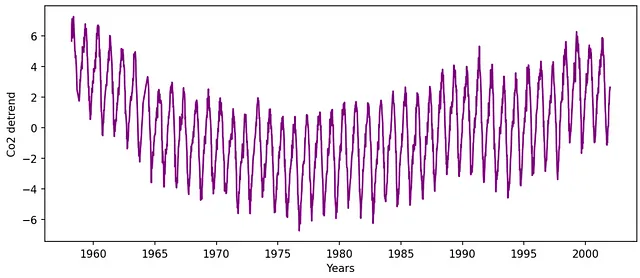
高速フーリエ変換アルゴリズム（FFT）を使用してFTを計算する：

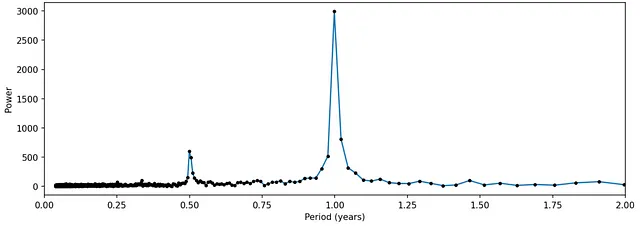
したがって、系列を構成する周波数を取得することができ、この場合は1年ごとと半年ごとの2つの異なるピークが見えます。これはデータセットの明確な季節性の視覚化です。

ただし、もっとも興味深いのは、時系列に摂動がある場合です。これは、イベントや外部変数（例えば近くの火山噴火）の影響である可能性があります。これをシミュレートするために、同じ系列に確率的なサイン波を追加します：

系列のFTを取得するためにFFTを適用する：

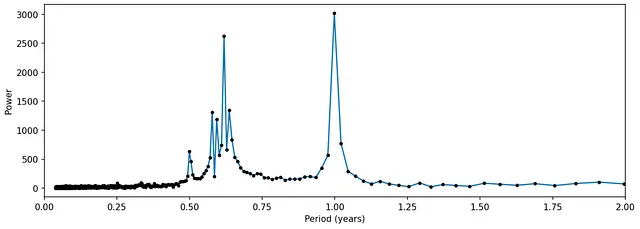
今、0.5から0.75の間に別の一連のピークがあり、それは摂動によって引き起こされます。

2.2 制限事項

時折、摂動と周波数の変化がいつ起こったのか、または系列内の各周波数の時間的配置を知りたい場合があります。摂動のある系列と摂動のない系列でのシミュレーションでは、影響のほとんどが系列の始まりにあることが明確です。しかし、系列の視覚検査とFT情報だけでは、その摂動がいつ発生したのかわかりません。したがって、私たちは別のツールを見つける必要があります。

しかし、フーリエ変換（FT）にはトレードオフがあります：不確定性原理により、時間情報が剥奪され、これらの周波数が系列でどのように現れるかを知ることができません。 これが不確定性原理が登場する場所です。周波数または時間のいずれかの無限の精度を追求する代わりに、バランスを保ちながら、低い解像度で両方の数量の洞察を得ることができるようにするため、不確定性原理を利用することができます。

3. 時間と周波数のトレードオフのためのウェーブレット変換

ウェーブレット変換（WT）は、時間と周波数の組み合わせであるF(t, ω)に関数f(t)を変換する解像度のバランスを取る手法として登場します。 WTの動作の詳細には触れませんが、要約すると、変換プロセスでは、異なるウェーブレット（既知の周波数と形状を持つ信号）を使用して、2つの関数の内積による時間の同期を時系列と一致させます。したがって、周波数と時間的な発生を把握することができますが、両方の数量の解像度が低下します。

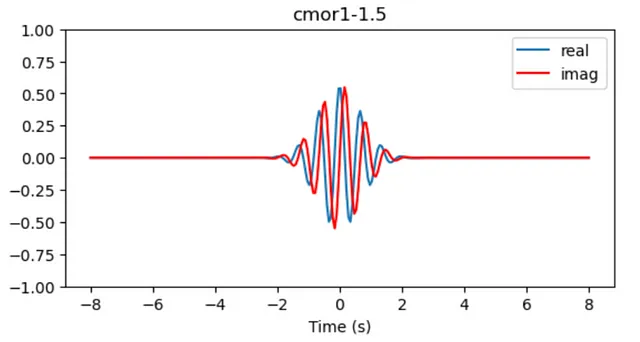
信号のウェーブレット変換を可視化するために、x軸を時間スケール、y軸を周波数スケール、カラースケールを周波数のパワーとして表現するのが一般的です。

トレンドのない時系列データに対しては、

視覚的な検査で予想通り、季節性が年毎に繰り返されることが明確にわかります。しかし、FTからの1年周期の大きなピークはより広くなり、値に対する確信度が低下しました。

最も興味深い分析は、シミュレーションされたシナリオに対して行われます。

ウェーブレット変換は、FTで観察される低周波数の摂動が系列の初期年に現れ、20-25年後に重要な影響を与えることを示しています。時間と周波数の両方で解像度が低下しますが、周波数の発生に関する新しい情報は価値があり、さまざまな質問に答えることができます。

4. 結論

要するに、不確定性原理は時間系列解析において基本的な制約を課します。フーリエ変換の制約から明らかになるように、フーリエ変換は時系列データから周波数情報を効率的に抽出しますが、それらの周波数が発生する時期に関する知識を犠牲にします。したがって、ウェーブレット変換は、原理に固有の不確実性を受け入れつつ、時間と周波数の解像度のトレードオフを行い、周波数成分の時間的な発生を洞察する有用なツールです。

謝辞

この素晴らしいビデオはArtem Kirsanovさんからのインスピレーションで、この記事を書くきっかけとなりました。このトピックについてさらに深く学びたい場合は、ビデオもご覧いただくことをおすすめします。

備考

• フーリエ変換（FT）は、量子力学や時系列解析においてだけでなく、この瞬間にもクラウドサービスにこの記事のデータを保存するために使用されています。最も有名で使用されているアルゴリズムの1つは、高速フーリエ変換（FFT）と呼ばれ、現代のデータ圧縮の基盤となっています。
• 物質の性質を数学的にモデル化するために、不確定性原理によってフーリエ変換が量子力学に自然に現れます。この原理によって自然の理解にもたらされる根本的な視点の変化に反映されます。粒子の位置を測定すると、その同じ粒子の速度に関する情報を失うことになり、逆もまた同様です。

この記事のノートブックはこちらで入手できます。

参考文献

[1] https://en.wikipedia.org/wiki/Uncertainty_principle

[2] https://www.statsmodels.org/dev/datasets/generated/co2.html (パブリックドメイン)

[3] ウェーブレット変換（Wikipedia）

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!