ロジスティック回帰における行列とベクトルの演算
ロジスティック回帰の行列とベクトルの演算
ベクトル化されたロジスティック回帰
人工ニューラルネットワーク(ANN)アルゴリズムの基礎的な数学は理解するのが難しい場合があります。また、モデルのバッチトレーニング中に使用されるフィードフォワードおよびバックプロパゲーション計算を表すために使用される行列およびベクトル演算は、理解の負担を増やす可能性があります。簡潔な行列およびベクトル表記は理にかなっていますが、そのような表記を通じて行列演算の微妙な動作の詳細まで追究することで、より明確さが得られます。私は、そのような微妙な詳細を理解するための最善の方法は、最小限のネットワークモデルを考慮することです。ネットワークの内部構造を理解するためには、ロジスティック回帰よりも優れたアルゴリズムはないと考えました。なぜなら、ロジスティック回帰には、多次元の入力、ネットワークの重み、バイアス、前方伝搬操作、非線形関数を適用する活性化関数、損失関数、勾配ベースのバックプロパゲーションなど、ANNの特徴として重要な要素がすべて含まれているからです。このブログでは、ロジスティック回帰モデルにおいて核となる行列およびベクトル演算のメモと調査結果を共有することを目的としています。
ロジスティック回帰の概要
ロジスティック回帰は、その名前に反して、回帰アルゴリズムではなく分類アルゴリズムです。通常、バイナリ分類のために使用され、例えば、メールがスパムかどうかを予測するためのインスタンスが属するクラスの確率を予測します。そのため、ロジスティック回帰では、依存または目的変数はカテゴリ変数と見なされます。例えば、メールがスパムである場合は1であり、スパムでない場合は0で表されます。ロジスティック回帰モデルの主な目標は、入力変数(特徴)と目的変数の確率の関係を確立することです。例えば、メールの特徴を入力特徴のセットとして与えられた場合、ロジスティック回帰モデルはそのような特徴とメールがスパムである確率の関係を見つけます。’Y’が出力クラス(メールがスパムであることなど)を表し、’X’が入力特徴を表す場合、確率はπ = Pr( Y = 1 | X, βi)のように指定できます。ここで、βiはロジスティック回帰パラメータを表し、モデルの重み’wi’およびバイアスパラメータ’b’を含みます。効果的には、ロジスティック回帰は、入力特徴の線形結合にシグモイド関数と呼ばれるS字型のロジスティック関数を適用して、0から1の確率を予測します。インスタンスの出力クラスを決定する一般的なアプローチは、予測確率のしきい値を設定することです。例えば、予測確率が0.5以上であれば、インスタンスはクラス1に属すると分類されます。それ以外の場合は、クラス0と分類されます。
ロジスティック回帰モデルは、モデルをトレーニングデータに適合させ、損失関数を最小化してパラメータを調整することでトレーニングされます。損失関数は、出力クラスの予測確率と実際の確率の差を推定します。ロジスティック回帰モデルのトレーニングで最も一般的に使用される損失関数は、ロジスティック損失関数またはバイナリクロスエントロピー損失関数として知られています。ロジスティック損失関数の式は次のとおりです:
L = — ( y * ln(p) + (1 — y) * ln(1 — p) )
ここで:
- Lはロジスティック損失を表します。
- yは正解のバイナリラベル(0または1)です。
- pは出力クラスの予測確率です。
ロジスティック回帰モデルは、勾配降下法などの手法を使用して損失関数を最小化し、パラメータを調整することによってパラメータを調整します。入力特徴とその正解クラスラベルのバッチが与えられた場合、モデルのトレーニングはエポックと呼ばれる複数のイテレーションで行われます。各エポックでは、モデルは前方伝搬操作を実行して損失を推定し、後方伝搬操作を実行して損失関数を最小化し、パラメータを調整します。エポック内のすべての操作では、行列およびベクトル演算が使用されます。
行列とベクトルの表記
ここで注意しておいてください このブログでは、数式や行列/ベクトルの表現を画像として埋め込むためにLaTeXスクリプトを使用しています 。LaTeXスクリプトに興味がある方は、お気軽にご連絡ください。共有いたします。
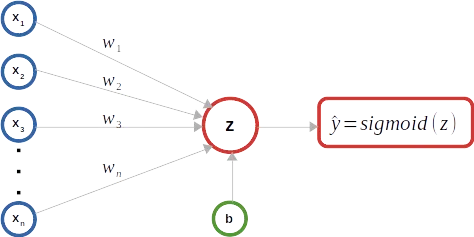
上記の図式に示されているように、2値ロジスティック回帰分類器は、イラストをシンプルに保つための例として使用されています。以下に示すように、行列Xは「m」個の入力インスタンスを表しています。各入力インスタンスは「n」個の特徴から構成され、行列X内の入力特徴ベクトルとして表されます。したがって、行列Xは(n x m)のサイズを持つ行列です。上付き文字(i)は行列X内の入力ベクトルの序数を表しています。下付き文字「j」は入力ベクトル内の特徴の序数インデックスを表しています。サイズが(1 x m)の行列Yは、行列X内の各入力ベクトルに対応する真のラベルを捉えます。モデルの重みは、入力ベクトルの各特徴に対応する「n」個の重みパラメータからなるサイズが(n x 1)の列ベクトルWで表されます。行列/ベクトルの演算を説明するために、バイアスパラメータ「b」は1つしかないため、サイズが(1 x m)で、同じバイアスbパラメータの「m」個を含む行列Bが考慮されます。
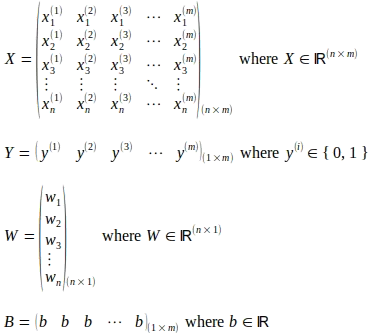
順方向伝播
順方向伝播操作の最初のステップは、モデルパラメータと入力特徴の線形結合を計算することです。このような行列演算の表記は以下のようになります。新しい行列Zが評価されます:
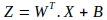
重み行列Wの転置の使用に注意してください。行列展開表現では、上記の操作は以下のようになります:
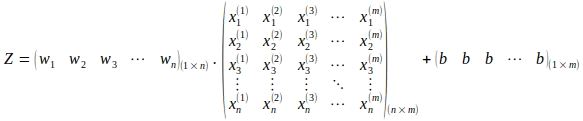
上記の行列演算により、以下に示すように、サイズが(1 x m)の行列Zが計算されます:

次のステップは、計算された線形結合にシグモイド関数を適用することで活性化を導出することです。次の行列演算により、サイズが(1 x m)の活性化行列Aが得られます。
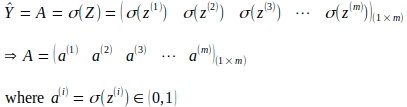
逆方向伝播
逆方向伝播またはバックプロパゲーションは、各エポックの終了時に不正確な予測によって引き起こされる全体のエラーや損失に各パラメータが与える貢献を計算する技術です。個々の損失の貢献は、損失関数の各モデルパラメータに関する勾配を計算することで評価されます。関数の勾配または導関数は、他のパラメータを定数として考えるときの関数の変化の速度または傾きを示します。特定のパラメータ値または点で評価されるとき、勾配の符号は関数が増加する方向を示し、勾配の大きさは傾斜の急峻さを示します。以下に示すような対数損失関数は、一つのグローバル最小点を持つ鉢状の凸関数です。そのため、ほとんどの場合、対数損失関数のパラメータに関する勾配は、グローバル最小値とは反対方向を指します。勾配が評価されると、各パラメータの値は勾配降下法と呼ばれる技術を使用して更新されます。
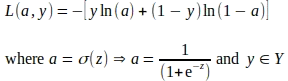
各パラメータの勾配は、連鎖律を使用して計算されます。連鎖律により、他の関数から構成される関数の導関数を計算することができます。ロジスティック回帰の場合、対数損失関数Lは活性化「a」と真のラベル「y」の関数であり、「a」自体は重み「w」とバイアス「b」の線形関数である「z」のシグモイド関数であり、損失関数Lは以下に示すように他の関数から構成される関数です。
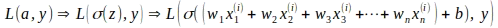
偏微分の連鎖律を用いると、重みとバイアスパラメータの勾配は以下のように計算できます:
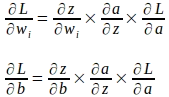
単一の入力インスタンスに対する勾配の導出
一度にパラメータを更新する際に関与する行列とベクトルの表現を見る前に、まず単一の入力インスタンスを使用して勾配を導出し、その表現の基礎をよりよく理解します。
‘a’と‘z’が、グラウンドトゥルースのラベル‘y’を持つ単一の入力インスタンスの計算された値を表すと仮定すると、損失関数の‘a’に関する勾配は以下のように導出されます。この勾配は、後でパラメータの勾配を導出するための連鎖律を評価するために必要な最初の量です。
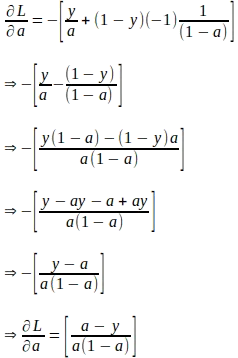
損失関数の‘a’に関する勾配が得られたら、以下の連鎖律を使用して損失関数の‘z’に関する勾配を導出できます:
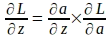
上記の連鎖律から、‘a’に関する‘z’の勾配も導出する必要があることがわかります。‘a’は‘z’にシグモイド関数を適用することで計算されます。したがって、シグモイド関数の式を使用して‘a’に関する‘z’の勾配を以下のように導出できます:
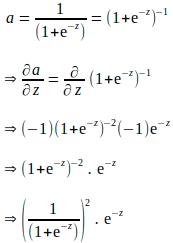
上記の導出は‘e’を用いて表現され、‘a’に関する勾配を評価するために追加の計算が必要であるように見えます。‘a’はフォワードプロパゲーションの一環として計算されることを知っているため、上記の導関数を‘a’に関して完全に表現することで、追加の計算を排除することができます:
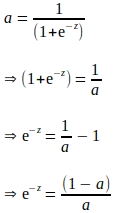
‘a’で表される上記の項目を代入すると、‘a’に関する‘z’の勾配は以下のようになります:
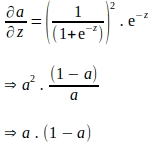
損失関数の‘a’に関する勾配と‘a’に関する‘z’の勾配が得られたので、損失関数の‘z’に関する勾配を以下のように評価できます:
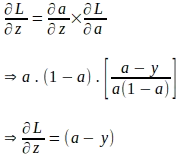
‘z’に関する損失関数の勾配を評価するためには長い道のりを経てきました。まだ、モデルパラメータに関する損失関数の勾配を評価する必要があります。‘z’はモデルパラメータと入力インスタンス‘x’の特徴量の線形結合であることを知っています:
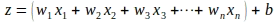
連鎖律を使用して、損失関数の重みパラメータ‘wi’に対する勾配が以下のように評価されます:
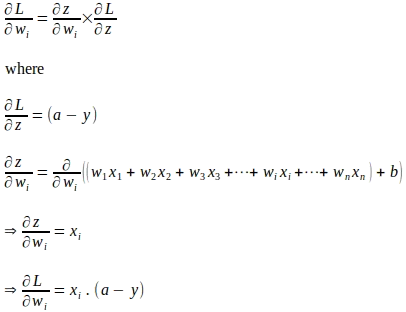
同様に、損失関数の‘b’に対する勾配が以下のように評価されます:
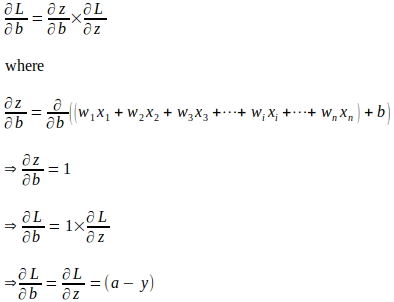
勾配を使用したパラメータの更新の行列とベクトル表現
単一の入力インスタンスを使用して導出されたモデルパラメータの勾配式を理解したので、トレーニングバッチ全体を考慮した行列とベクトル形式で式を表現できます。まず、以下の式で与えられる損失関数に対する ‘z’ に関する勾配をベクトル化します:
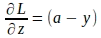
上記のベクトル形式は、すべての ‘m’ 個のインスタンスに対するものです:
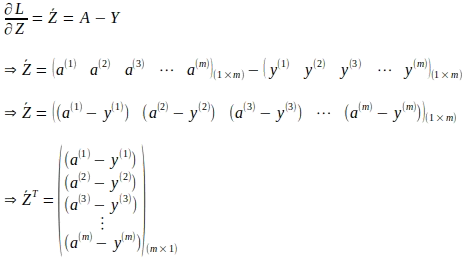
同様に、各重み ‘wi’ に対する損失関数の勾配もベクトル化できます。単一のインスタンスに対する重み ‘wi’ に対する損失関数の勾配は次のようになります:
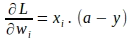
上記のベクトル形式は、すべての ‘m’ 入力インスタンスにわたるすべての重みに対して評価され、次のように ‘m’ 個の勾配の平均として表されます:
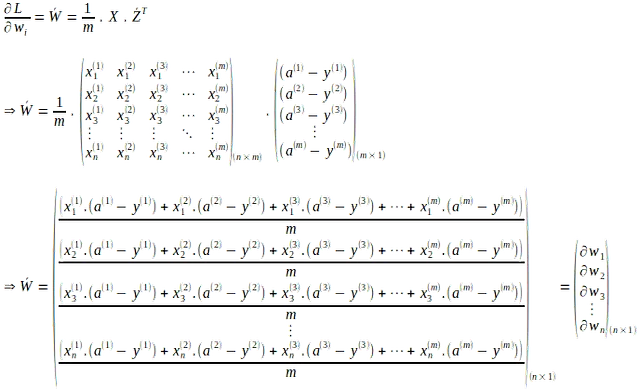
同様に、すべての ‘m’ 入力インスタンスにわたる ‘b’ に対する損失関数の勾配は、各個別インスタンスの勾配の平均として計算されます:
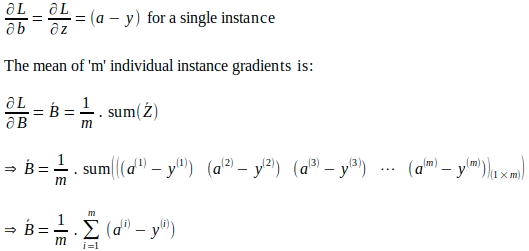
モデルの重み勾配ベクトルとバイアスの全体的な勾配が与えられた場合、モデルパラメータは次のように更新されます。以下に示すパラメータの更新は、学習率を使用した勾配降下法と呼ばれる技術に基づいています。学習率は、勾配降下法などの最適化技術において、計算された勾配に基づいて各エポックで行われるモデルパラメータの調整のステップサイズを制御するためのハイパーパラメータです。学習率は、効果的にスケーリングファクターとして機能し、最適化アルゴリズムの速度と収束に影響を与えます。

結論
このブログで示されている行列とベクトルの表現から明らかなように、ロジスティック回帰は、このような行列とベクトル演算の微妙な動作の詳細を理解するための最小限のネットワークモデルを可能にします。ほとんどの機械学習ライブラリは、このような細かい数学的な詳細をカプセル化しており、代わりに前方または後方伝播などのより高いレベルで定義されたプログラミングインターフェースを公開しています。これらのライブラリを使用してモデルを開発するためには、すべての細かい詳細を理解する必要はありませんが、このような詳細は、このようなアルゴリズムの数学的な直感に光を当てることができます。ただし、このような理解は、ANN、再帰ニューラルネットワーク(RNN)、畳み込みニューラルネットワーク(CNN)、生成的対抗ネットワーク(GAN)などの他のモデルに基づいた数学的な直感を展開するのに確かに役立ちます。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles






