ランキング評価指標の包括的ガイド

ランキング評価指標のガイド

豊富なメトリックの選択肢を探索し、問題に最適なものを見つける

はじめに

ランキングは、機械学習の問題であり、ユーザーに最も適した方法でドキュメントのリストを並べ替えることを目的としています。つまり、最も関連性の高いドキュメントがトップに表示されるようにします。ランキングは、レコメンデーションシステムから始まり、アルゴリズムが購入するためのアイテムのセットを提案する場合から、NLPの検索エンジンに至るまで、データサイエンスのさまざまなドメインで登場します。

自然に生じる疑問は、ランキングアルゴリズムの品質をどのように推定するかということです。古典的な機械学習と同様に、任意のタスクに適した単一の普遍的なメトリックは存在しません。なぜなら、各メトリックには、与えられた問題の性質とデータの特性に依存する適用範囲があるからです。

そのため、どの機械学習の問題にも成功裏に取り組むために、主要なメトリックを把握することが非常に重要です。この記事では、まさにそれを行います。

• 「LangChainを使用して、強力な大規模言語モデルを使用してデータフレームをクエリしてください」
• 「機械学習を使用するかどうか」
• データサイエンス入門：初心者向けガイド

ただし、先に進む前に、なぜ一部の一般的なメトリックは通常ランキング評価に使用されないべきかを理解しましょう。これらの情報を考慮することで、他のより高度なメトリックの存在の必要性を理解しやすくなります。

注：この記事と使用されている数式は、Ilya Markov氏のオフライン評価に関するプレゼンテーションに基づいています。

メトリック

この記事では、いくつかの情報検索メトリックについて説明します：

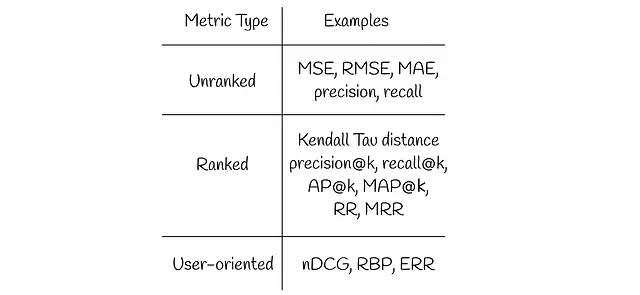
非ランク付けメトリック

映画の評価を予測し、ユーザーに最も関連性の高い映画を表示するレコメンデーションシステムを想像してみてください。評価は通常、正の実数を表します。最初の見た目では、MSE（RMSE、MAEなど）のような回帰メトリックが、ホールドアウトデータセット上でシステムの品質を評価するための合理的な選択肢に思えます。

MSEは、すべての予測された映画を考慮し、真のラベルと予測されたラベルの平均二乗誤差を測定します。しかし、ユーザーは通常、ウェブサイトの最初のページに表示されるトップの結果にのみ関心があります。これは、標準の回帰メトリックによっても同様に評価される低い評価の映画が検索結果の最後に表示されることを意味します。

以下の単純な例は、1つの検索結果のペアを示し、それぞれのMSE値を測定しています。

第2の検索結果の方がMSEが低いですが、ユーザーはそのようなレコメンデーションに満足しません。関連性の低いアイテムだけを最初に見ることで、ユーザーは最初の関連性の高いアイテムを見つけるまで下までスクロールする必要があります。そのため、ユーザーエクスペリエンスの観点からは、第1の検索結果の方がはるかに優れています：ユーザーはトップのアイテムに満足し、それに進むだけです。

同じ論理は、すべてのアイテムを考慮する分類メトリック（精度、再現率）にも適用されます。

すべての説明されたメトリックに共通しているのは何でしょうか？すべてのアイテムを均等に扱い、高い関連性と低い関連性の結果の違いを考慮しないという点です。そのため、これらのメトリックは非ランク付けと呼ばれています。

上記の2つの類似する問題例を経験することで、ランキング指標を設計する際に注目すべき側面がより明確になります：

ランキング指標は、より関連性の高い結果に重みを置き、関連性の低い結果を低下させるか無視するべきです。

ランク付け指標

ケンドール・タウ距離

ケンドール・タウ距離は、ランクの逆転の数に基づいています。

逆転は、ドキュメントのペア（i、j）で、ドキュメントiがドキュメントjよりも関連性が高く、検索結果で後に表示されることを示します。

ケンドール・タウ距離は、ランキング内の逆転の数を計算します。逆転の数が少ないほど、検索結果は良いものです。この指標は論理的に見えるかもしれませんが、以下の例で示されているようなデメリットもあります。

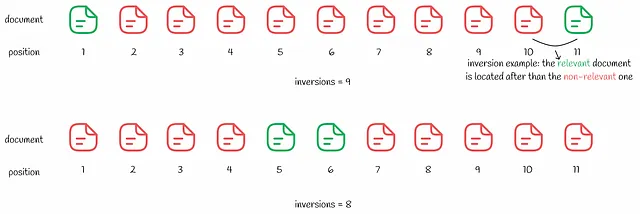
1つ目の例に比べて2つ目の検索結果は8つの逆転しかないため、より良いように見えます。MSEの例と同様に、ユーザーは最初の関連する結果にのみ興味があります。2番目の場合は、関連性のない検索結果をいくつか経験するため、ユーザーエクスペリエンスは1番目の場合よりも悪くなります。

Precision@k & Recall@k

通常の適合率と再現率の代わりに、特定の上位の推薦数kだけを考慮することも可能です。この場合、指標は低いランクの結果には関心を持ちません。選択したkの値によって、対応する指標はそれぞれprecision@k（「kでの適合率」）とrecall@k（「kでの再現率」）として表されます。その数式は以下に示されています。

上位kの結果がユーザーに表示され、各結果が関連するかどうかを考えます。precision@kは、上位kの結果の中で関連する結果の割合を測定します。同時に、recall@kは、上位kの中での関連する結果を全データセット内の関連アイテムの総数に対する割合で評価します。

これらの指標の計算プロセスをより良く理解するために、以下の例を参照しましょう。

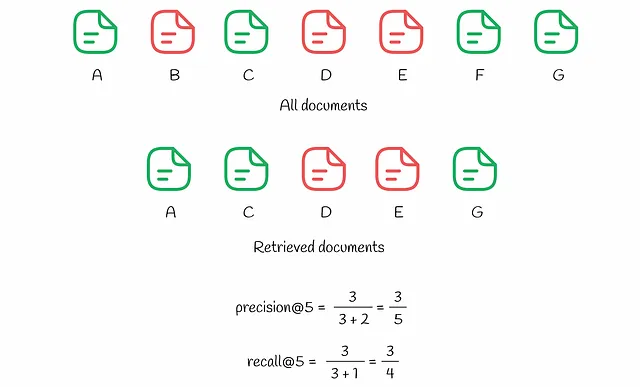
システムには7つのドキュメント（AからGと名付けられたもの）があります。予測に基づいて、アルゴリズムはユーザーのためにその中からk = 5つのドキュメントを選択します。上位k = 5つの中には3つの関連ドキュメント（A、C、G）があり、これによりprecision@5は3/5になります。同時に、recall@5は全データセット内の関連アイテムを考慮に入れます：それらは4つあり（A、C、F、G）、recall@5 = 3/4となります。

recall@kは常にkの成長とともに増加し、この指標はいくつかのシナリオでは実際にはあまり客観的ではありません。システム内のすべてのアイテムがユーザーに表示されるエッジケースでは、recall@kの値は100％になります。一方、precision@kはrecall@kと同じ単調性を持っていません。これは、precision@kがトップkの結果に関連し、全システム内の関連アイテムの数に関連してランキングの品質を測定するためです。客観性は、実践ではrecall@kよりも通常は好まれる指標の1つです。

AP@k（平均適合率）＆MAP@k（平均平均適合率）

バニラのprecision@kの問題は、関連するアイテムが取得されたドキュメントの中でどのような順序で表示されるかを考慮していないことです。たとえば、10個の取得されたドキュメントの中に関連するものが2つある場合、precision@10は、これら2つのドキュメントの位置に関係なく常に同じになります。たとえば、関連するアイテムが位置（1、2）または（9、10）にある場合、このメトリックは両方の場合を区別せず、precision@10が0.2となります。

しかし、実際の生活では、システムは下部ではなく上部にランク付けされた関連ドキュメントにより高い重みを与える必要があります。この問題は、平均精度（AP）と呼ばれる別のメトリックによって解決されます。通常の精度と同様に、APは0から1の値を取ります。

AP@kは、i番目のドキュメントが関連する場合、iが1からkまでのすべての値のprecision@iの平均値を計算します。

上の図では、同じ7つのドキュメントが表示されています。クエリQ₁への応答では、k = 5の取得されたドキュメントがあり、そのうち3つの関連ドキュメントがインデックス（1、3、4）に配置されています。これらの位置iごとに、precision@iが計算されます：

• precision@1 = 1 / 1
• precision@3 = 2 / 3
• precision@4 = 3 / 4

他の不一致したインデックスiは無視されます。AP@5の最終値は、上記の精度の平均として計算されます：

• AP@5 = (precision@1 + precision@3 + precision@4) / 3 = 0.81

比較のために、3つの関連ドキュメントが上位kに含まれる別のクエリQ₂への応答を見てみましょう。それにもかかわらず、今回は前の場合よりも上位（位置（1、3））に関連しないドキュメントが2つあり、それによりAP@5が0.53となります。

時には、単一のクエリではなく複数のクエリでアルゴリズムの品質を評価する必要があります。そのために、平均平均精度（MAP）が利用されます。MAPは、複数のクエリQのAPの平均値を単純に取ります：

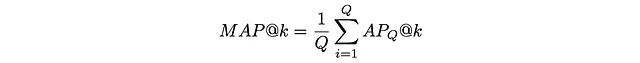
以下の例では、3つの異なるクエリに対してMAPがどのように計算されるかを示しています：

RR（Reciprocal Rank）とMRR（Mean Reciprocal Rank）

ユーザーは時に、最初の関連結果にのみ興味を持つことがあります。Reciprocal rankは、最初の関連結果がトップからどれだけ遠いかを示す0から1の値を返すメトリックです：ドキュメントが位置kにある場合、RRの値は1 / kです。

APとMAPと同様に、平均逆順位（MRR）は、複数のクエリの平均RRを測定します。

以下の例では、3つのクエリに対してRRとMRRが計算されています：

ユーザー指向のメトリクス

ランク付けメトリクスはアイテムのランキング順位を考慮するため、ランク付けされていないメトリクスよりも好ましい選択肢ですが、重要なデメリットがあります：ユーザーの行動に関する情報が考慮されていません。

ユーザー指向のアプローチでは、ユーザーの行動についての特定の仮定を行い、それに基づいてランキング問題に適したメトリクスを生成します。

DCG（割引累積利得）＆nDCG（正規化割引累積利得）

DCGメトリクスの使用は次の仮定に基づいています：

高い関連性を持つドキュメントは、検索エンジンの検索結果リストで早く表示されるほど（ランクが高いほど）有用です — Wikipedia

この仮定は、ユーザーが上位の検索結果をより評価する方法を自然に表現しています。

DCGでは、各ドキュメントには特定のドキュメントの関連性を示す利得が割り当てられます。各アイテムの真の関連性Rᵢ（実際の値）が与えられた場合、利得を定義するためのいくつかの方法が存在します。最も一般的な方法の1つは次のようなものです：

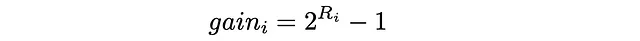
基本的に、指数関数は関連性の高いアイテムに重点を置いています。たとえば、映画の評価が0から5までの整数で割り当てられる場合、評価に対応する各映画は、評価が1つ減少した映画と比較して、おおよそ2倍の重要性を持つことになります：

それに加えて、ランキング位置に基づいて各アイテムは割引値を受け取ります：アイテムのランキング位置が高いほど、対応する割引値も高くなります。割引は、アイテムの利得を比例的に減少させるペナルティとして機能します。実際には、割引は通常、ランキングインデックスの対数関数として選択されます：

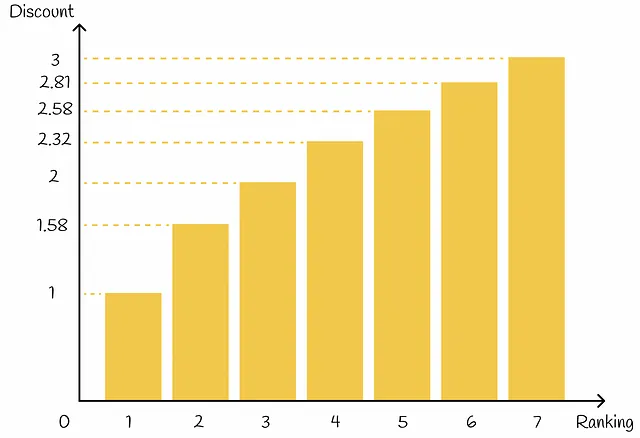
最後に、DCG@kは、最初のk個の取得したアイテムすべてに対する利得と割引の合計として定義されます：

上記の式でgainᵢとdiscountᵢを置き換えると、式は次のようになります：

DCGメトリクスをより解釈しやすくするために、完璧なランキングの場合におけるDCGₘₐₓの最大値で正規化することが通常行われます。その結果得られるメトリクスはnDCGと呼ばれ、0から1の値を取ります。

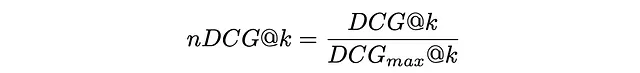
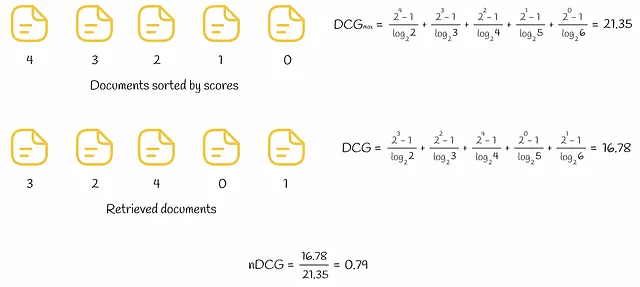
下の図では、5つのドキュメントに対するDCGとnDCGの計算の例が示されています。

RBP（Rank-Biased Precision）

RBPのワークフローでは、ユーザーはすべての可能なアイテムを調べる意図を持っていません。代わりに、ユーザーは確率pで一つのドキュメントから次のドキュメントに進み、逆の確率1−pで現在のドキュメントで検索手続きを終了します。各終了の決定は独立しており、検索の深さに依存しません。行われた研究によれば、このようなユーザーの行動は多くの実験で観察されています。検索効果の測定のためのRank-Biased Precisionの情報に基づいて、以下のダイアグラムでワークフローを示すことができます。

パラメータpは持続性と呼ばれます。

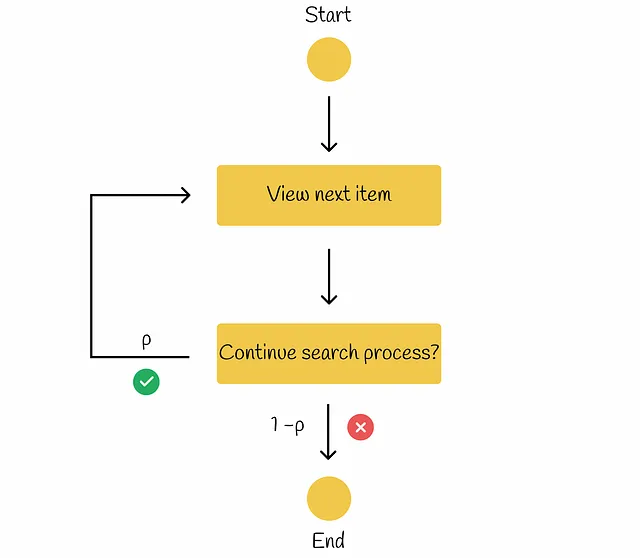
このモデルでは、ユーザーは常に1番目のドキュメントを見ます。次に確率pで2番目のドキュメントを見、確率p²で3番目のドキュメントを見るといった具合に進みます。最終的に、ドキュメントiを見る確率は次のようになります：

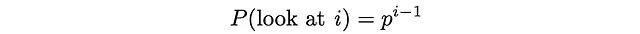
ユーザーは、ドキュメントiを見るのは、ドキュメントiが既に見られたドキュメントであり、検索手続きが確率1−pで直ちに終了する場合にのみです。

その後、見られるドキュメントの期待値を推定することができます。0 ≤ p ≤ 1なので、以下の級数は収束し、式は以下の形式に変形できます：

同様に、各ドキュメントの関連性Rᵢを与えられた場合、期待ドキュメントの関連性を求めることができます。期待関連性の値が高いほど、ユーザーは調べるドキュメントにより満足するでしょう。

最後に、RPBは期待ドキュメントの関連性（有用性）を期待されるチェックされたドキュメントの数で割ったものとして計算されます：

RPBの定式化により、値は0から1の間になります。通常、関連性スコアはバイナリタイプ（ドキュメントが関連している場合は1、それ以外は0）ですが、0から1までの実数値を取ることもあります。

システム内のユーザーがどれだけ持続的かに基づいて、適切なpの値を選ぶべきです。pの値を見つけるのが困難な場合は、いくつかの実験を実行し、最も効果的なpを選ぶことが良いです。

ERR（期待相互順位）

その名前が示すように、この指標は多くのクエリにわたる平均相互順位を測定します。

このモデルはRPBに似ていますが、少し異なる点があります。現在のアイテムがユーザーにとって関連性がある（Rᵢ）場合、検索手順は終了します。それ以外の場合、アイテムが関連性がない場合（1−Rᵢ）、確率pでユーザーは検索プロセスを続けるかどうかを決定します。続ける場合、検索は次のアイテムに進みます。そうでない場合、ユーザーは検索手順を終了します。

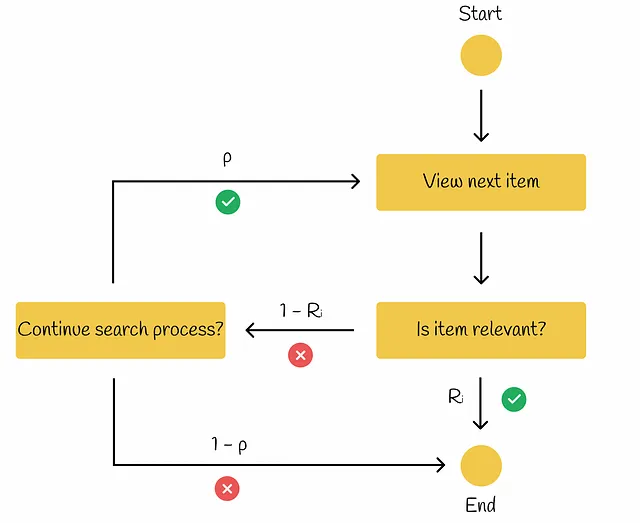
Ilya Markov氏によるオフライン評価のプレゼンテーションによれば、ERRの計算式を見つけましょう。

まず、ユーザーが文書iを見る確率を計算しましょう。基本的には、すべてのi-1個の前の文書が関連性を持たず、各イテレーションでユーザーが確率pで次のアイテムに進んだことを意味します：

ユーザーが文書iで停止する場合、この文書はすでに見られており、確率Rᵢでユーザーが検索手順を終了したことを意味します。このイベントに対応する確率は、実際には相互順位が1/iと等しいことと同じです。

これ以降、期待値の式を使用するだけで、期待相互順位を推定することができます：

パラメータpは通常1に近い値が選択されます。

RBPの場合と同様に、Rᵢの値は0から1の範囲のバイナリまたは実数のいずれかです。以下の図は、6つのドキュメントのセットに対するERRの計算例です。

左側では、取得されたすべてのドキュメントが関連性に基づいて降順に並べられ、最良のERRが得られます。右側の状況とは対照的に、ドキュメントは関連性に基づいて昇順に表示され、最悪のERRが生じます。

ERRの式では、すべての関連性スコアが0から1の範囲にあることを前提としています。初期の関連性スコアがその範囲外から与えられる場合、それらを正規化する必要があります。最も一般的な方法の1つは、指数関数的に正規化することです：

結論

情報検索における品質評価に使用される主要な指標について説明しました。ユーザー指向の指標がより頻繁に使用される理由は、実際のユーザーの行動を反映しているからです。また、nDCG、BPR、ERRの指標は、他の指標と比較してより多くの関連性レベルで動作するため、より汎用性があります。AP、MAP、MRRのような指標は、バイナリの関連性レベルのみを対象としているためです。

残念ながら、これらの指標のすべてが不連続またはフラットであり、問題のあるポイントでの勾配が0になるか、定義されていないため、ほとんどのランキングアルゴリズムはこれらの指標を直接最適化することは困難です。ただし、この領域では多くの研究が行われ、この問題を解決するための多くの高度なヒューリスティクスが最も一般的なランキングアルゴリズムの裏に現れています。

リソース

• Kendall Tau距離 | Wikipedia
• ランクバイアス精度による検索効果の測定
• 割引累積利得 | Wikipedia
• ランクバイアス精度の不確実性
• 情報検索、オフライン評価 | Ilya Markov

特記しない限り、すべての画像は著者によるものです。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!