ランキングアルゴリズム入門

検索結果をソートするための主なランキングアルゴリズムについて学ぶ

イントロダクション

ランキング学習（LTR）は、クエリに関連する項目のリストをソートすることを目的とした教師あり機械学習アルゴリズムの一種です。古典的な機械学習では、分類や回帰などの問題では、特徴ベクトルに基づいて単一の値を予測することが目標です。LTRアルゴリズムは、特徴ベクトルのセット上で動作し、アイテムの最適な順序を予測します。

LTRにはさまざまな応用があります。以下にいくつかの例を挙げます:

検索エンジン。ユーザーがブラウザの検索バーにクエリを入力します。検索エンジンは、最も関連性の高い結果がトップに表示されるようにウェブページをランク付けする必要があります。
レコメンドシステム。入力クエリに基づいて、どの映画をユーザーに推奨するべきかを選択する映画レコメンドシステム。

では、ランキング問題を形式的に定義しましょう:

n次元の特徴ベクトルにクエリとドキュメントの情報を格納する場合、ランキングの目的は、クエリとドキュメントの関連性を示す実数を出力する関数fを見つけることです。さらに、オブジェクトiがオブジェクトjよりも高い順位にランク付けされている場合（i ▷ j）、f(i)はf(j)よりも大きくなければなりません。

注記: i ▷ jはドキュメントiがドキュメントjよりも高い順位にランク付けされていることを意味します。

データ

特徴ベクトル

特徴ベクトルは、次の3つのタイプの特徴から構成されます:

ドキュメントのみから派生する特徴（例: ドキュメントの長さ、ドキュメント内のリンクの数）。
クエリのみから派生する特徴（例: クエリの長さ、クエリの頻度）。
ドキュメントとクエリの組み合わせから派生する特徴（例: TF-IDF、BM25、BERT、ドキュメントとクエリの共通単語の数）

トレーニングデータ

モデルをトレーニングするためには、モデルに供給されるトレーニングデータが必要です。トレーニングデータの収集方法に基づいて、2つのアプローチがあります。

オフラインLTR。データは人間によって手動で注釈されます。人間は、さまざまなクエリとドキュメントに対して（クエリ、ドキュメント）の関連性を評価します。このアプローチは費用がかかり時間がかかりますが、高品質な注釈を提供します。
オンラインLTR。データはユーザーのクエリ結果との相互作用から暗黙的に収集されます（例: ランク付けされたアイテムへのクリック数、ウェブページ上での滞在時間）。この場合、トレーニングデータを取得するのは簡単ですが、ユーザーの相互作用は容易に解釈できません。

その後、特徴ベクトルとそれに対応するラベルがあります。これがモデルをトレーニングするために必要なすべてです。次のステップは、問題に最適な機械学習アルゴリズムを選択することです。

ポイントワイズランキング

ポイントワイズアプローチでは、各特徴ベクトルに対して個別にスコアを予測します。最終的に、予測されたスコアがソートされます。予測に使用するモデル（決定木、ニューラルネットワークなど）のタイプは重要ではありません。

このタイプのランキングは、ランキング問題を回帰タスクに変換し、回帰モデルが選択した損失関数（例: MSE）に基づいて正しい関連性を予測しようとします。

別の妥当なアプローチは、グラウンドトゥルーランキングをワンホット表現に変換し、このデータをモデルに供給することです。この場合、回帰モデルまたは分類モデル（クロスエントロピー損失）のいずれを使用することが可能です。

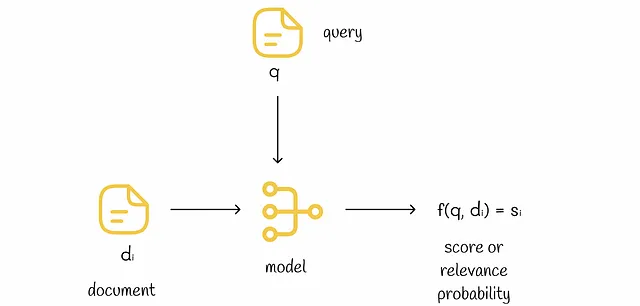
Pointwiseモデルのアーキテクチャ。入力として、モデルはクエリと特徴ベクトルを受け入れます。

非常にシンプルな方法ですが、以下にいくつかの問題があります。

クラスの不均衡

ポイントワイズ法を使用する際に一般的な問題は、クラスの不均衡です。実際の生活でランダムなクエリを取る場合、コレクション内の全てのドキュメントのごく一部だけがそれに関連している可能性が非常に高いです。したがって、訓練データ内のクエリに対する関連ドキュメントと非関連ドキュメントの間には高い不均衡があります。

この問題を克服することは可能ですが、考慮すべきより深刻な問題があります。

最適化メトリックの問題

ポイントワイズランキングには、最適化目的に関して根本的な問題があります:

ポイントワイズランキングはドキュメントのスコアを独立して最適化し、異なるドキュメント間の相対スコアを考慮しません。そのため、ランキングの品質を直接最適化することはありません。

以下の例を考えてみましょう。ポイントワイズアルゴリズムが2つのドキュメントセットに対して予測を行ったとします。訓練中にMSE損失が最適化されると仮定します。

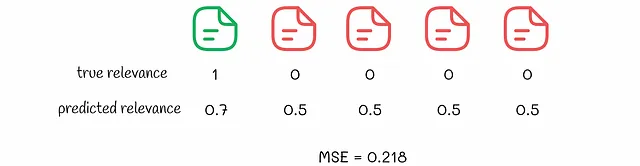
コレクションには1つの関連ドキュメントと他の4つの非関連ドキュメントが含まれています。関連ドキュメントの予測関連度は0.7で、他のドキュメントは0.5です。

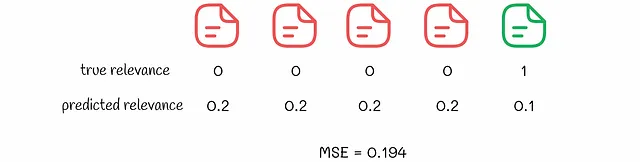
コレクションには1つの関連ドキュメントと他の4つの非関連ドキュメントが含まれています。関連ドキュメントの予測関連度は0.1で、他のドキュメントは0.2です。

2つのランキング結果を見ると、アルゴリズムの観点からは、2つ目のランキングの方が優れているとされます。なぜなら、対応するMSE値がより低いからです。しかし、2番目のランキングを選ぶと、ユーザーには最初に全ての非関連結果が表示されます。ところが、最初の例では、関連結果が最初に表示され、ユーザーエクスペリエンスからはずっと良いです。通常、ユーザーはその後に推奨されたものにあまり注意を払いません。

この例は、実際の生活では最初に関連する結果を表示すること、およびアイテムの相対順序についてより関心があることを示しています。ポイントワイズでは、ドキュメントの独立した処理ではこれらの側面を保証することはありません。低い損失はより優れたランキングとは等価ではありません。

ペアワイズランキング

ペアワイズモデルは、各イテレーションで2つのドキュメントを対象に動作します。入力形式に応じて、2つのタイプのペアワイズモデルがあります。

ペア入力モデル

モデルへの入力は2つの特徴ベクトルです。モデルの出力は、最初のドキュメントが2番目のドキュメントよりも高い順位にランク付けされる確率です。訓練中、これらの確率は異なる特徴ベクトルのペアに対して計算されます。モデルの重みは、真の順位に基づいて勾配降下法によって調整されます。

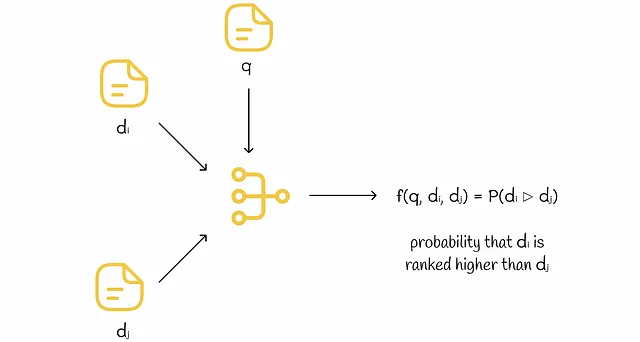
この方法には推論中に2つの主な欠点があります:

推論中に特定のクエリに対してn個のドキュメントをランク付けするために、これらのドキュメントの各ペアをモデルで処理してすべてのペアワイズ確率を取得する必要があります。ペアの総数は二次的です（n *（n-1）/ 2となります）ので、非常に効率が悪いです。
すべてのドキュメントのペアワイズ確率を持っていても、特にドキュメントの三つ組（x、y、z）があり、モデルによって次のようにランク付けされる場合など、どのように最終的にランク付けするかは明らかではありません：x ▷ y、y ▷ z、z ▷ x。

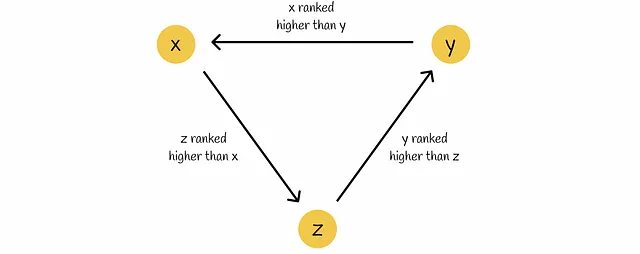
これらの欠点のため、ペア入力モデルは実践ではほとんど使用されず、単一入力モデルが優先されます。

単一入力モデル

モデルは単一の特徴ベクトルを入力として受け取ります。トレーニング中、ペア内の各ドキュメントは個別にモデルにフィードされ、独自のスコアを受け取ります。その後、両方のスコアを比較し、モデルはグラウンドトゥルースの順位に基づいて勾配降下法によって調整されます。

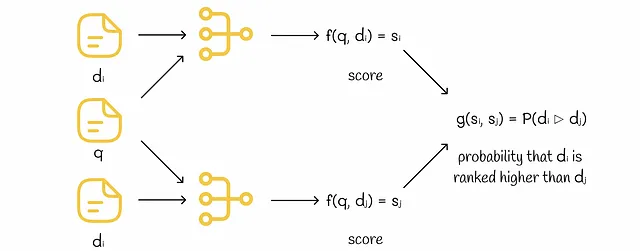
推論中、各ドキュメントはモデルに渡されてスコアが与えられます。スコアはソートされ、最終的なランキングが得られます。

Siameseネットワーク（FaceNet、SBERTなど）に詳しい方にとって、単一入力モデルはSiameseネットワークと考えることができます。

ペアワイズ損失関数

各トレーニングイテレーションで、モデルはドキュメントのペアに対してスコアを予測します。そのため、損失関数はペアワイズであり、両方のドキュメントのスコアを考慮する必要があります。

一般的に、ペアワイズ損失は、2つのスコアs[i]とs[j]の差の定数σを乗じたzを引数とします。アルゴリズムによって、損失関数は以下のいずれかの形式を取ることがあります。

時にはスコアの差zを定数で乗じることもあります。

RankNetは最も人気のあるペアワイズランキングアルゴリズムの一つです。次のセクションでその実装の詳細を見ていきます。

RankNet

ドキュメントiとjのスコアを取得した後、RankNetはsoftmax関数を使用してそれらを正規化します。これにより、RankNetはドキュメントiがドキュメントjよりも上位にランク付けされる確率P[i][j] = P(i ▷ j)を得ます。逆に、確率P̃[j][i] = P(j ▷ i) = 1 — P(i ▷ j)を計算することもできます。単純化のために、現実ではiがjよりも上位にランク付けされていると仮定しましょう。したがって、P̃[i][j] = 1およびP̃[j][i] = 0です。モデルの重みの更新には、RankNetは以下のように単純化された交差エントロピー損失を使用します。

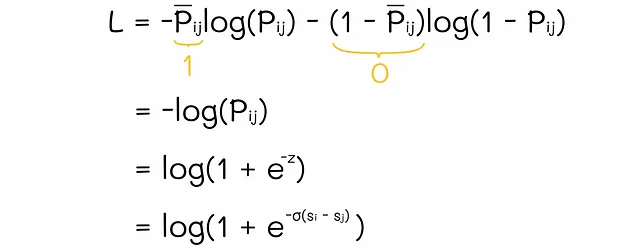
モデルの重みは勾配降下法によって調整されます。次回、モデルが同じドキュメントiとjのペアを受け取ると、ドキュメントiのスコアは以前よりも高くなり、ドキュメントjはおそらく下げられるでしょう。

RankNetの分解

単純化のため、数学に深く入り込むことはしませんが、元の論文で興味深い研究結果が発表されています。著者たちは訓練プロセスを簡素化する方法を見つけ、変数S[i][j]を導入しました。この変数は3つの可能な値のいずれかを取ります：

いくつかの数学的なトリックの後、交差エントロピー損失の導関数は次のように因数分解されます：

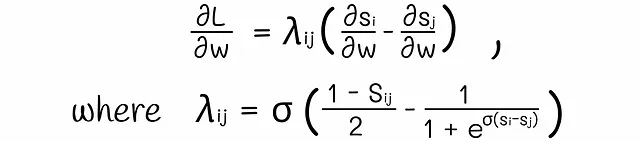
式中のλは、すべてのドキュメントのペアに対して比較的高速に計算できる定数です。正または負の値を取ることで、これらのλはドキュメントを上または下に押し出す力として機能します。

単一のドキュメントiに対して、すべてのペアワイズなλを合計することができます。この合計は、ランキングにおいてドキュメントiに適用される総力を表します。

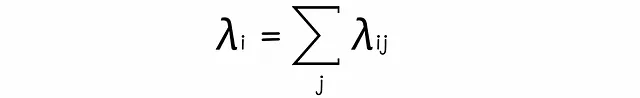
λを直接扱うことで、トレーニング時間が短くなり、結果の解釈が向上します。

ペアワイズアルゴリズムはポイントワイズアプローチよりも優れた性能を発揮しますが、2つの欠点があります。

解釈可能な確率ではない

モデルの出力確率は、モデルが特定のオブジェクトiがオブジェクトjよりも高い順位にランク付けされる自信度を示しています。しかし、これらの確率は実際ではなく、モデルによっておおまかに近似されることがあります。したがって、特に前述のような循環的なケースでは常に解釈に使用するのは良い考えではありません。

インバージョンの最小化が最適ではない

この問題は、前の問題よりもはるかに重要です。ほとんどのペアワイズアルゴリズムや特にRankNetの基本的な問題は、ランクのインバージョンの数を最小化することです。インバージョンの数を最適化することは自然に思えるかもしれませんが、それが実際にほとんどのエンドユーザーが望むことではありません。次の例を考えてみましょう。どちらの順位があなたの意見では良いと思いますか？

2番目の順位はインバージョンが少ないため、アルゴリズムの優先順位ですが、通常のユーザーは最初の順位を好むでしょう。少なくとも1つの関連結果が上位にあるため、ユーザーは多くのドキュメントをスクロールして最初の関連結果を見つける必要がありません。同様に、nDCGやERRなどのユーザー指向のメトリックを使用する方が、インバージョンの数よりも上位の結果により重点を置くため、より良い結果が得られるでしょう。

結果として、すべてのドキュメントのペアが同じ重要度を持つわけではありません。アルゴリズムは、トップの正しい順位にはるかに重要度を置くように調整する必要があります。

論文の研究者は、RankNetでランキングを最適化することがどのように最適な結果につながるかをよく説明した例を示しています。

1位のドキュメントが4位に押し出され、15位のドキュメントが10位に押し出されたため、インバージョンの合計数は2つ減少しました。しかし、ユーザーの体験からすると、新しい順位は悪くなりました。核心の問題は、RankNetが悪い位置にあるドキュメントに大きな勾配を割り当てることです。しかし、ユーザー指向のメトリックを最適化するためには、これが逆に機能する必要があります。良い位置にあるドキュメントは、悪い位置にあるドキュメントよりもさらに上に押し出されるべきです。このようにすることで、nDCGなどのユーザー指向のメトリックが高くなります。

リストワイズランキング

リストワイズアルゴリズムは、ランキングメトリックを明示的に最適化します。勾配降下法で特定のメトリックを最適化するためには、そのメトリックの導関数を計算する必要があります。残念ながら、nDCGや精度などのほとんどのランキングメトリックは連続的でなく微分可能ではないため、他の高度な手法が考案されています。

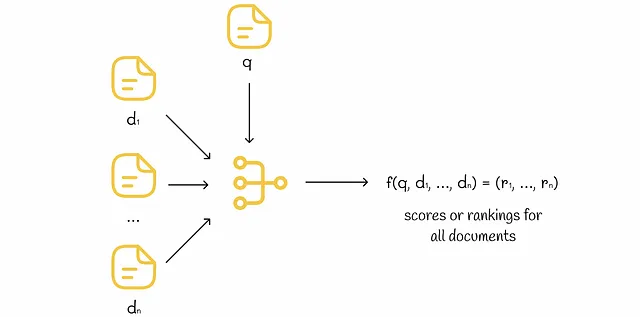
ポイントワイズやペアワイズのランキングとは異なり、リストワイズの手法は一度に複数のドキュメントのリストを入力として受け取ります。これにより、大きな計算が必要になることもありますが、各イテレーションでアルゴリズムにより多くの情報が提供されるため、より堅牢性が高くなります。

リストワイズモデルのアーキテクチャ。入力として、クエリとすべてのドキュメントの特徴ベクトルを取ります。

LambdaRank

実装によっては、LambdaRankはペアワイズまたはリストワイズの方法として考えられることがあります。

nDCGに焦点を当てると、nDCGが高くなるようにドキュメントの位置を交換したペアに対してより大きな勾配を割り当てることが最適です。この核心のアイデアがLambdaRankにあります。

アルゴリズムの名前にある「lambda」は、最適化のためにRankNetで説明されたλも使用していることを示唆しています。

研究者たちは素晴らしい結果を出し、RankNetの損失値に|nDCG|を掛けると、アルゴリズムはnDCGを直接最適化する傾向があることを実証しました！つまり、LambdaRankアルゴリズムは、この場合にはRankNetと非常に似ていますが、この時にはλにnDCGの変化が乗算されます：

研究の魅力的な点は、このトリックがnDCGだけでなく、他の情報検索メトリックにも適用できることです！同様に、λに精度の変化を乗算すると、精度が最適化されます。

最近、LambdaRankが特定の情報検索メトリックの下限を最適化することが理論的に証明されました。

その他の手法

他のリストワイズの手法の詳細については議論しませんが、2つの優れたアルゴリズムの実装の背後にある主要なアイデアを提供します。

LambdaMartは、LambdaRankから派生した損失関数を使用して勾配ブースティングツリーを使用するリストワイズアプローチの有名な実装です。実際には、LambdaRankよりも優れたパフォーマンスを発揮します。

SoftRankは、nDCGの導関数の存在問題に対処します。これにより、nDCGを滑らかに表現し近似する新しいメトリック「SoftNDCG」を作成し、対応する導関数を見つけてモデルの重みを勾配降下法で更新することが可能になります。実際には、このアプローチは他のメトリックにも同様に適用できます。

結論

ランキングは、オブジェクトの関連順に並べるための機械学習における重要なタスクです。ポイントワイズやペアワイズの手法はあまり使用されませんが、リストワイズの手法は最も堅牢です。明らかに、私たちはランキングアルゴリズムのごく一部しか議論していませんが、この情報はListNetやListMLEなどのより複雑な技術を理解するために不可欠です。リストワイズアルゴリズムの広範なリストはこちらで見つけることができます。

LambdaRankは、特定のメトリックを最適化するための多くの柔軟性を提供する現在の最先端のランキングアルゴリズムの1つです。

ランキングメトリックについてさらに情報を見つけたい場合は、このトピックに関する私の他の記事をおすすめします。

参考文献

From RankNet to LambdaRank to LambdaMART: An Overview
Learning to Rank using Gradient Descent
Information Retrieval | Learning to Rank | Harrie Oosterhuis
Learning to Rank | Wikipedia
SoftRank: Optimising Non-Smooth Rank Metrics

すべての画像は特記されていない限り、著者によるものです。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!

Data scienceDeep DivesInformation RetrievalRecommendation SystemSearch Engines

Was this article helpful?

93 out of 132 found this helpful