モンテカルロ近似法:どれを選び、いつ選ぶべきか?
モンテカルロ近似法の選択とタイミング
逆変換、ランダムウォークメトロポリス・ヘイスティングス、またはギブス? 数学的基礎、Pythonによるスクラッチからの実装、および各メソッドの利点/欠点に焦点を当てた分析
近似サンプリングの紹介
実用的な確率モデルのほとんどにおいて、正確な推論は扱いにくいため、何らかの近似手法に頼る必要があります。
— パターン認識と機械学習¹
確率モデルにおいて、確定論的推論はしばしば扱いにくいため、数値サンプリングに基づく近似手法であるモンテカルロテクニックに頼ることがあります。これらの手法によって、確率分布p(z)が与えられたときのターゲット関数f(z)の期待値を計算するという鍵となる問題に取り組みます。期待値の簡単な定義は、次のような積分です:
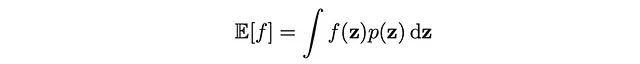
後ほど見ていくように、これらの積分は計算的に複雑すぎるため、この記事ではサンプリング手法に取り組むことにします。
この記事では、3つの主要なサンプリング手法、すなわち逆変換、マルコフ連鎖モンテカルロ(MCMC)、およびギブスサンプリングについて説明します。これらの手法の基礎的な統計的性質と計算要件を理解することで、次のことを学びます:
- 逆変換サンプリングは、既知かつ単純な分布からのデータのシミュレーションにおいて、特に低次元の場合に高い精度で適しています。
- ランダムウォークメトロポリス・ヘイスティングスは、複雑な多峰性または未知の分布に最適であり、グローバルな探索と/または収束が優先される場合に使用されます。具体的には、対称分布に対してはメトロポリス・ヘイスティングスの特定のインスタンスであるメトロポリスアルゴリズムが使用されます。
- ギブスサンプリングは、条件付き分布を容易にサンプリングできる高次元の問題に最適であり、効率が重視されます。
目次
- 逆変換サンプリング• アルゴリズムの動作原理• Pythonによる実装• 必要条件• 利点と欠点
- マルコフ連鎖モンテカルロ• メトロポリス・ヘイスティングス・アルゴリズム• 特別なインスタンス:対称分布のためのメトロポリス・アルゴリズム• 利点と欠点
- ギブス• アルゴリズム• 条件• ギブスとメトロポリス・ヘイスティングスの関係
- 比較:変換 vs. メトハス vs. ギブスの利点と欠点
1. 変換手法:逆累積分布関数
逆変換サンプリングは、その名前が示すように、目的の分布に従うランダムな数値を生成するために、対象分布の逆累積分布関数(CDF)を使用します。基本的なアイデアは次の通りです:
- 一様乱数を生成する:0から1までの一様分布から数値Uを抽出します。
- 逆CDFを適用する:目的分布の逆CDFを使用して、Uを目的分布に従うサンプルに変換します。
以下は、サンプル(青)が分布(赤)から描かれる様子を簡単に示したものです:
逆CDFは、正規分布、指数分布、ガンマ分布、ベータ分布など、CDFが既知である分布からサンプリングするための計算的に単純かつ汎用性のある手法です。
PDF、CDF、および逆CDF
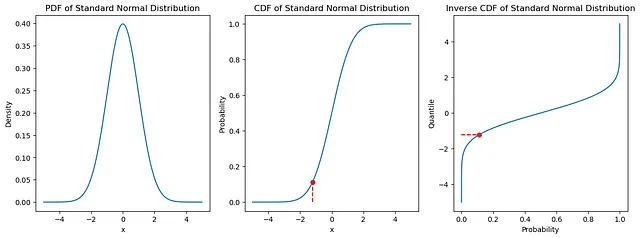
直感的には、CDFはPDFの累積値であり、PDFの積分と等しいです。そして、CDF関数の逆を取ることで、この手法で使用される最終的な逆CDFを得ます。
形式的には、aがランダム変数である場合、aのCDFは次のように与えられます:
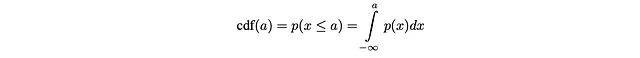
CDF Fは次の主な特性を持ちます:
- Fは連続的である
- Fは非減少である
- Fはすべてのa∈Rに対して0 ≤ cdf(a) ≤ 1の範囲を持つ
逆CDFアルゴリズムはどのように動作しますか?
このアルゴリズムは次の要素で構成されています:
入力:
U:Uは0から1の間で引かれる一様乱数変数です。- これは逆CDFの入力確率であり、所望の分布からのサンプルに変換されます。
パラメータ:
F:目標分布のCDF。- Fを使用して、単純にその逆のF^-1を計算し、入力値を所望の範囲にマップすることができます。
出力:
x:目標分布から引かれたランダムサンプル。- これは一様分布(入力)の乱数に逆CDFを適用することで生成されます。
Pythonの実装
さて、ゼロからこの方法を実装しましょう。指数関数を使用すると、逆CDFによって描かれたサンプルを視覚化し、正確な分布と比較するのが簡単です:
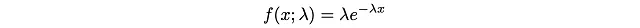
標準の微積分の統合技術により、目標CDF F(x)は次のようになります:

このCDFの逆は次のようになります:
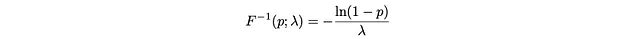
逆CDFのメソッドを使用して5000個のサンプルを生成します:
import numpy as npimport matplotlib.pyplot as plt# ラムダ=1の指数分布の逆CDFdef inverse_cdf(p): return -np.log(1 - p)# 逆CDFを使用して1000個のサンプル値を生成するuniform_samples = np.random.uniform(0, 1, 1000)transformed_samples = inverse_cdf(uniform_samples)# x値と真のPDFを生成するx_values = np.linspace(0, np.max(transformed_samples), 1000)pdf_values = np.exp(-x_values)
逆CDFアルゴリズムが動作するための要件
逆CDFメソッドは、以下の重要な仮定を行います:
- CDF Fは逆関数可能でなければなりません:CDF Fは逆関数可能でなければなりません。つまり、Fへの各入力は一意の出力を持つ必要があります。
この制約により、いくつかの関数が除外されます。たとえば、以下は一般的ですが逆関数可能ではない(したがって逆CDFとは動作しない)いくつかの関数の種類です:
- 定数関数:定数関数f(x) = c(cは定数)は逆関数可能ではないため、すべての入力が同じ出力にマップされ、関数が一対一ではないとなります。
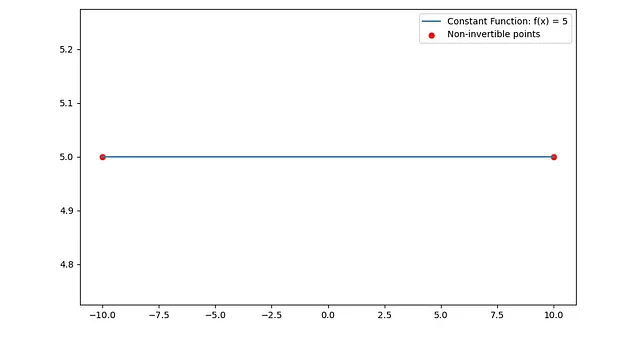
2. 特定の二次関数:たとえば、f(x) = x^2は逆関数可能ではないです(f(x) = 1を考えてみてください、xは1または-1になります)。
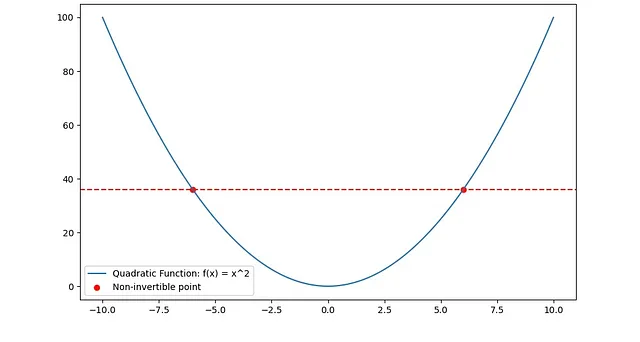
3. 特定の三角関数:たとえば、f(x) = sin(x)は、周期的であるため、その全ての定義域上で逆関数可能ではありませんが、制約された定義域では逆関数可能になる場合があります。
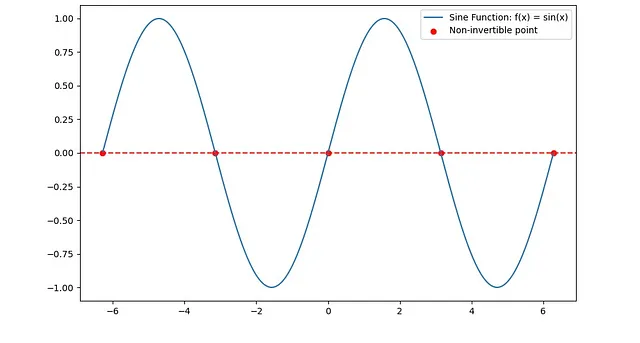
逆CDFはなぜ動作するのか?
重要なアイデアは、0から1の範囲で一様分布するランダム変数が、目標分布の逆関数を適用することで特定の分布を持つランダム変数に変換できるということです。この逆関数は既知で扱いやすいと仮定されています。
利点
- アルゴリズムのシンプルさ:低次元のデータで非常に簡単に実装できるため、さまざまな領域とタスクに広く適用できます。
- サンプルの精度:CDFとその逆関数が正確に目標分布を表していると仮定した場合、この方法は他の方法(MCMCなど)と比べて比較的高い精度を提供します。
欠点
- 計算の複雑さ:一部の分布では、逆CDFに閉じた形式の式が存在しないため、計算が困難または費用がかかる場合があります。
- 高次元の難しさ:変数間の依存関係を含む高次元空間で適用することは困難です。
- 逆関数可能の制約:CDFが逆関数可能でない場合、このメソッドは無効になります。上記で見たように、これにはいくつかの関数が含まれます。
- 既知の分布に限定される:逆CDFは正確なCDFの形式を必要とするため、既知の分布にのみ適用できます。
これらの制限を考慮すると、逆CDFを適用できる分布のカテゴリはわずかです。実際には、ビッグデータや未知の分布では、この方法はすぐに使用できなくなる可能性があります。
これらの利点と欠点を考慮して、これらの制限に対処する別のランダムサンプリングフレームワークを見てみましょう:マルコフ連鎖モンテカルロ(MCMC)。
2. マルコフ連鎖モンテカルロ(MCMC)
さきほど見たように、逆CDF変換法は非常に制限されています、特に高次元の標本空間では。一方、マルコフ連鎖モンテカルロ(MCMC)は次元の高いデータに対してもスケーリングが可能で、より多くの分布からサンプリングすることができます。

メトロポリス・ヘイスティングスアルゴリズムはどのように機能するのですか?
直感的には、アルゴリズムは次の手順で機能します:逆CDFと同様に、サンプリングしているターゲット分布があります。ただし、追加の要素が必要です:現在の状態z*、およびq(z|z*)はz*に依存し、サンプルz¹, z², z³などのマルコフ連鎖を作成します。各サンプルは、特定の基準を満たす場合にのみチェーンに受け入れられます。アルゴリズムのバリエーションによってこの基準が異なるため、以下で定義します。
アルゴリズムをよりアルゴリズム的な構造に具体化しましょう。
アルゴリズムはサイクルで動作し、各サイクルは次の手順に従います:
- 提案分布からサンプルz*を生成します。
- サンプルを確率で受け入れます。この値を受け入れ確率と呼び、メトロポリス・ヘイスティングスでは以下のように定義されます:
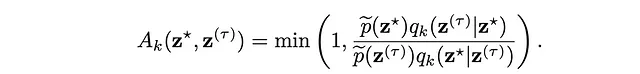
where
- z*は現在の状態です。
- z^Tは提案された新しい状態です。
- p(z*)は望ましい分布に従って状態z*の確率です。
- p(z^T)は望ましい分布に従って状態z^Tの確率です。
この受け入れ閾値の背後にあるロジックは、望ましい分布に基づくより確率が高い状態がより頻繁に訪れることを保証するものです。
これはアルゴリズムの最も一般化されたバージョンです。提案分布が対称であることがわかっている場合、つまり、状態xからx′への移行を提案する確率と、x′からxへの移行を提案する確率が同じである場合、すなわちq(x′|x) = q(x|x′)である場合、より単純な受け入れ閾値を必要とするメトロポリス・ヘイスティングスの特別なケースを使用することができます。
対称分布のメトロポリスアルゴリズム
これは、提案分布が対称である場合に使用する特定のMCMCアルゴリズムです。つまり、すべての値1および0の場合に、q(z⁰ | z¹) = q(z¹ | z⁰)と解釈される「任意の状態Aから状態Bに遷移する確率は、BからAに遷移する確率と等しい」となります。したがって、アルゴリズムの各ステップは次のようになります:
- 提案分布からサンプルz*を生成します。
- 以下の確率でサンプルを受け入れます:

メトロポリス・ヘイスティングスおよびメトロポリスアルゴリズム
アルゴリズムを並べて見てみましょう。前に見たように、唯一の違いは受容閾値で、アルゴリズムの他のステップはすべて同じように実行されます。

利点
- 平衡分布への収束:特定の場合において、ランダムウォークは所望の平衡分布に収束することがありますが、高次元空間では時間がかかる可能性があります。
- 低い計算コスト:ランダムウォークは他の複雑なサンプリング方法に比べて少ない計算リソースを必要とすることが多く、計算効率が優先される問題に適しています。
- 応用の多様性:自然発生パターンに高い類似性を持つため、ランダムウォークはさまざまな分野で利用されています。
• 物理学:液体や気体中の分子のブラウン運動
• ネットワーク分析
• 金融市場:株価の動きのモデリング
• 集団遺伝学
欠点
- 初期化に対して敏感:アルゴリズムのパフォーマンスは、開始値の選択に対して敏感になることがあります。特に初期化された値が高密度エリアから遠い場合にはそうです。
- 局所的なトラップ:提案分布の複雑さに応じて、アルゴリズムは局所最適解に陥り、分布に沿って他の領域に移動するのが困難になることがあります。
さて、メトロポリス・ヘイスティングスアルゴリズムを念頭に置いて、それの別の特別なインスタンスであるギブスサンプリングを見てみましょう。
3. ギブスサンプリング
ギブスサンプリングは、メトロポリス・ヘイスティングスの特別なインスタンスであり、各ステップが常に受容される特徴があります。まず、ギブスサンプリングアルゴリズム自体を見てみましょう。
ギブスアルゴリズムはどのように動作するのか?
アイデアは比較的シンプルで、3つの変数に関する分布p(z1, z2, z3)からサンプリングするというマイクロな例を拡大して説明するのが最善です。アルゴリズムは次のステップで実行されます:
- 時刻Tで、開始値を初期化します:
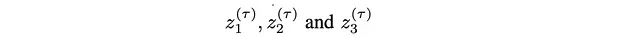
2. z1の新しい値を抽出します:

3. 2番目の位置z2の新しい値を条件付きで抽出します:
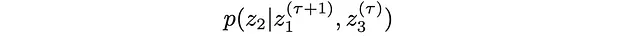
4. 最後の位置z3の新しい値を抽出します:

5. このプロセスを繰り返し、3つの変数z1…z3をサイクリングします。ある満足のいく閾値に到達するまで。
汎用アルゴリズム
形式的には、最初に開始位置を初期化し、T回の連続したステップを行います。

ギブスサンプリングが目標分布から正しくサンプリングするための条件
- 不変性。目標分布 p(z) は各ギブスステップで不変であり、したがって p(z) はマルコフ連鎖全体で不変である。
- エルゴード性。条件付き分布がすべてゼロでない場合、エルゴード性が意味される。なぜなら、z 空間の任意の点は有限なステップで到達可能であるからです。
- 十分なバーンイン。ランダムな初期化が必要な任意の手法と同様に、最初のいくつかのサンプルは初期化に依存し、多くの反復後に依存関係が弱まります。
これはメトロポリス・ヘイスティングスとどう関連していますか?
メトロポリス・ヘイスティングスでは、受け入れの閾値を以下のように定義しました:
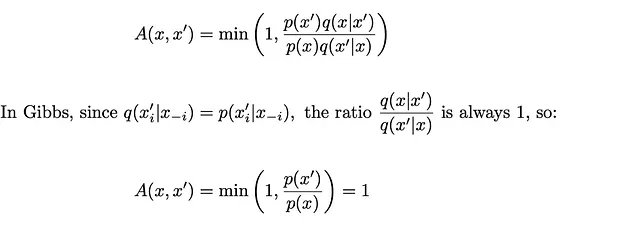
したがって、メトロポリス・ヘイスティングスの提案ステップは常に受け入れられます。これはギブスアルゴリズムでも見られるようになります。
変異
ギブス法では変数を一度に1つずつ更新するため、連続するサンプル間に強い依存関係があります。これを克服するために、ブロッキングギブスと呼ばれる方法を使用して、グループの変数ではなく個々の変数からサンプリングすることができます。
同様に、マルコフ連鎖の性質上、連続して描かれる例は相関しています。独立したサンプルを生成するために、シーケンス内でのサブサンプリングを使用することができます。
4. プロ/コン: 逆関数法 vs メトロポリス・ヘイスティングス vs ギブス
これまで各アルゴリズムの動作方法と適用範囲について説明してきましたが、それぞれの方法の特徴をまとめましょう。
1. 逆変換サンプリング
- データサイズ: 中程度のデータセットに最適。
- 時間: 一般的には単変量分布に対して効率的。
- データの複雑さ: 累積分布関数(CDF)とその逆関数が既知で計算しやすい単純な分布に使用する。
- 以下の場合は避けることを検討してください: 高次元変数/分布のサンプリング。
- 最大の利点: CDFが目標分布を正確に反映している場合、高い精度が得られる。
- 要件: CDFは既知で逆関数が存在する必要がある。
2. メトロポリス・ヘイスティングス(MCMC)
- データサイズ: 大規模なデータセットに対してスケーラブルで適しています。
- 時間: 目標分布の複雑さに応じて計算コストがかかる場合があります。
- データの複雑さ: 複雑または多峰性の分布に理想的です。
- 最大の利点: – 正規化定数(完全な形式)を知らなくても分布からサンプリングできること- 分布のグローバルな構造を探索するのに適しており、収束を保証する
- デメリット: – 複雑または多峰性の目標分布の場合、アルゴリズムが局所的なモードに閉じ込められ、それらの間の遷移が困難になるため、非常に遅い収束が起こる場合があります。- 変数が強く相関している場合- 高次元空間- 不適切な初期値やステップサイズの選択
3. ギブスサンプリング
- データサイズ: 小さなデータセットと大規模なデータセットの両方に適しています。
- 時間: 受け入れ/拒否ステップを必要としないため、ランダムウォークメトロポリス・ヘイスティングスよりも効率的です。
- データの複雑さ: 各変数の条件付き分布からサンプリングできるような高次元分布を扱う場合に最適です。
- 最大の利点: – 条件付き分布を簡単に計算できること- ランダムウォークに比べて局所的な最小値に陥りにくい。
- 要件: – マルコフ連鎖のエルゴード性 – 全条件付き分布が既知で扱いやすいこと
まとめ:
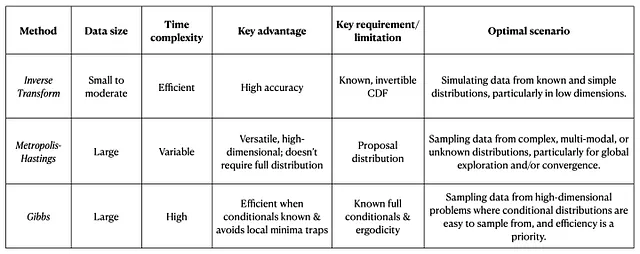
結論
ここまでお付き合いいただきありがとうございます!この記事では、3つの主要な近似サンプリング手法である逆CDF、メトロポリス・ヘイスティングスMCMC、およびギブスサンプリングMCMCについて見てきました。各アルゴリズムの機能、それぞれの利点と欠点、および一般的な使用例について探求しました。
逆CDFは、既知の分布からサンプリングするための直感的な手法を提供しますが、そのCDFが逆関数可能でない場合や高次元または複雑な分布には適していません。 メトロポリス・ヘイスティングスMCMCは、それ以外では扱いにくい分布からのサンプリングを可能にするより一般的なアプローチを提供します。ただし、より多くの計算リソースが必要であり、提案分布のような調整パラメータに対して敏感かもしれません。 ギブスサンプリングMCMCは、結合分布が複雑であるがより単純な条件付き分布に分解できる場合に特に効率的です。機械学習で広く使用されていますが、収束まで時間がかかる場合や高次元の問題に対してはメモリが多く必要です。
[1] Bishop, C. M. (2016). Pattern Recognition and Machine Learning (Softcover reprint of the original 1st edition 2006 (corrected at 8th printing 2009)). Springer New York.
*特に明記されていない限り、すべての画像は著者によって作成されています。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
- ChatGPTのためのエニグマ:PUMAは、LLM推論のための高速かつ安全なAIアプローチを提案するものです
- 「読むアバター:リアルな感情制御可能な音声駆動のアバター」
- 感情の解読:EmoTXによる感情と心の状態の明らかにする、新しいTransformer-Powered AIフレームワーク
- 『AI入門』
- 「カーシブと出会う:LLMとのインタラクションのためのユニバーサルで直感的なAIフレームワーク」
- デシは、コード生成のためのオープンソース1Bパラメータの大規模言語モデル「DeciCoder」を紹介します
- モデルの精度向上:Spotifyでの機械学習論文で学んだテクニック(+コードスニペット)





