ソートアルゴリズムの概要:マージソート
マージソートの概要
分割統治法を用いたソートの適用方法を理解する

はじめに
ソートに関して、マージソートは最も人気のあるアルゴリズムの一つです。これは有名な「分割統治法」のパラダイムに基づいており、大きな問題をより解決しやすい小さな問題に分割し、その解決策を元の問題に結合するものです。
このチュートリアルでは、実装の詳細とマージソートの計算量をビッグオーノーテーションで評価する方法について掘り下げます。さらに、理解を深めるために例も提供します。
アルゴリズム
このアルゴリズムのアイデアは、元の配列のより小さい部分配列を再帰的にソートすることです。いくつかの部分配列がソートされた後、それらはより大きなサイズの新しい配列に変換されます。この手順は、元の配列のソートされたバージョンが得られるまで続きます。
最初は複雑に見えるかもしれませんが、既にソートされた配列を基に新しいソートされた配列を得ることは比較的高速な手順です。
まず、マージ関数を見てみましょう。その後、それをアルゴリズムの最終バージョンで使用します。
マージ関数
マージ関数は、2つのソートされた部分配列を受け取り、それらの要素からなる新しいソートされた配列を返します。以下のコードスニペットでは、要素の配列が、2つのソートされた部分配列 array[left, middle] と array[middle + 1, right] として渡されます。
マージ関数
私たちは、i と j の2つのポインタを使用して、両方の配列の要素をループします。各イテレーションで array[i] と array[j] の要素を比較し、より小さい要素を new_array に追加します。その後、追加された要素に応じてポインタ i または j を増やし、次の要素を指すようにします。
ループは、どちらかのサブ配列のすべての要素が new_array に追加されるまで続きます。その後、もう一方のサブ配列に含まれるより大きな値を持つ残りの要素を単純に追加します。
最後に、ソートされた new_array の各要素を元の配列にコピーします。その結果、インデックス left から right のすべての要素が配列内でソートされます。
ここで、長さ N の2つのサブ配列に対して、各要素を線形に1回だけ通過することに注意しましょう。このメソッドの計算量は O(N) です。
マージの例
2つのソートされた部分配列 array[0:3] と array[4:7] からなる配列があるとします。最初に、最小の要素を指す2つのポインタ i と j を初期化します。この場合、それらはそれぞれインデックス 0 と 4 の要素を指します。
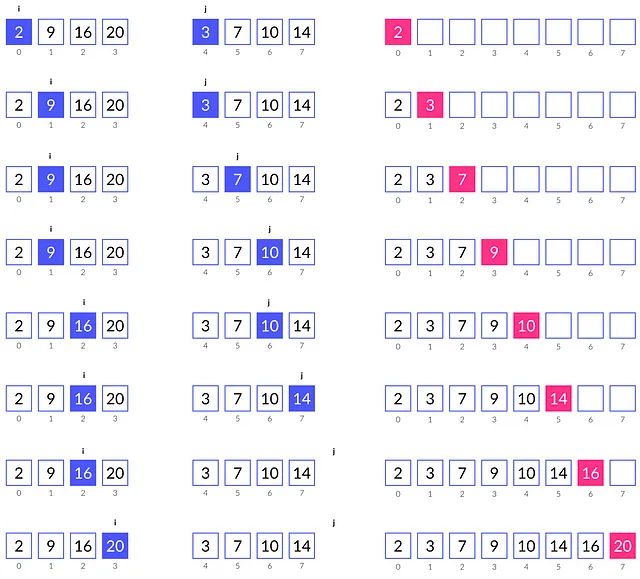
イテレーション 1。array[0] = 2 と array[4] = 3 を比較します。2 ≤ 3 なので、新しい配列の最初の要素として 2 を保存し、i を 1 増やして次の増加要素である 9 を指すようにします。
イテレーション 2。array[1] = 9 と array[4] = 3 を比較します。9 > 3 なので、新しい配列の2番目の要素として 3 を保存し、j を 1 増やして次の増加要素である 7 を指すようにします。
イテレーション 3。array[1] = 9 > array[5] = 7 です。次の要素として 7 を保存します。j は 1 増やされます。
…
イテレーション 7。j は右側の配列の終端を指しています。これは、左側の配列のインデックス i から始まるすべての要素が右側の配列のどの要素よりも大きいことを意味します。したがって、右側の配列から残りの要素(16 と 20)をすべて新しい配列にコピーします。
この手順が完了すると、新しい配列のソートされた値はすべて元の配列にコピーされます。
ソート関数
ソート関数は、左側と右側をそれぞれ別々にソートするために再帰的に自身を呼び出します。両方の半分がソートされると、merge_sort()関数呼び出しの後に結合されます。
マージソート関数
クライアントにとって関数のインターフェースをより便利にするために、merge_sort()の最初の関数呼び出しを別の関数にラップすることができます。これにより、クライアントは関数の左側と右側の引数を渡す必要がなくなり、カプセル化の設計原則に成功した関数を使用できます。
マージソート呼び出しを別の関数にラップする
例
要素数が8の配列に対するマージソートの階層的な呼び出しは、以下の図に示されています。まず、配列を長さ4の2つの等しい部分に分割します。それぞれの半分に対して、マージソートを再び呼び出します。これにより、サイズ2の配列が生成されます。ちなみに、単一要素からなる配列は常にソートされているため、これらの配列を再分割する必要はありません。

サイズ2の配列をソートすることでアルゴリズムを続行します。サイズ2の連続する2つの配列がソートされると、それらは長さ4の新しいソート済み配列にマージされます。このプロセスは、サイズ2のすべての配列に対して繰り返されます。サイズ4の連続する2つの配列がソートされると、それらは同様に長さ8の新しいソート済み配列にマージされます。
要素がすべてソートされるとプロセスを終了します。
計算量
計算量を評価するためには、再帰呼び出しの構造を理解する必要があります。ソートする必要があるサイズNの配列があるとします。
この配列をサイズN / 2の2つの半分に分割します。それぞれの半分をさらにN / 4の2つの小さな半分に分割します。その結果、N / 4のサイズの4つの配列が得られます。同様に、次のレベルでは、N / 8のサイズの8つの配列が得られます。このプロセスをサイズ1のN個の配列に到達するまで続けます。このプロセスは、以下の図で示されています。
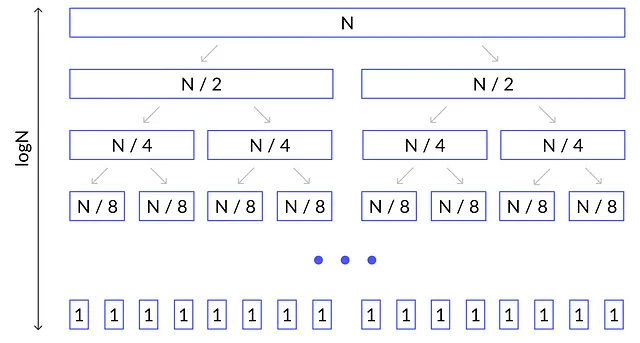
図の各配列に対して、O(K)の処理時間を必要とするマージ手順を呼び出す必要があります。ここでは、Kは配列の長さです。上記の図の各レベルの合計時間の計算を行いましょう。
- 最初のレベルでは、サイズNの単一の配列があり、O(N)の処理時間が必要です。
- 2番目のレベルでは、サイズN / 2の2つの配列があります。それぞれの配列にはO(N / 2)の時間が必要です。合計時間は2 * O(N / 2) = O(N)です。
- 3番目のレベルでは、サイズN / 4の4つの配列があります。それぞれの配列にはO(N / 4)の時間が必要です。合計時間は4 * O(N / 2) = O(N)です。
- 最後のレベルには、サイズ1のN個の配列が含まれています。それぞれの配列にはO(1)の時間が必要です。合計時間はN * O(1) = O(N)です。
このロジックに従うと、各レベルでO(N)の処理時間が必要であることがわかります。各ステップで配列が2つの半分に分割されるため、O(logN)のレベルが存在することも容易に気付けます。これにより、最終的な計算量はO(N) * O(logN) = O(N * logN)となります。
利点
- 効率性。マージソートの全体的な計算量はO(N * logN)です。これは、配列要素の比較に基づくすべてのソートアルゴリズムの中で最も良い計算量です。ただし、マージ手順では要素を一時的に別の配列にソートする必要があります。この配列のサイズは、両方のサブ配列の長さと同じであり、O(N)のメモリスペースを使用します。
- シンプルさ。他の効率的なソートアルゴリズムと比較して、マージソートは簡単に解釈や実装ができます。
- 安定なソート。初期の配列に等しい要素がある場合、マージソートアルゴリズムはそれらの相対位置を変更しません。これは、ソート部分を持つより複雑なアルゴリズムで使用される重要な特性です。
結論
私たちは、最も人気のあるソーティングアルゴリズムの一つを見てきました。これにより、分割統治の原則を理解することができました。さらに、マージソートはその単純さと効率的な複雑さを優雅に組み合わせており、多くのアプリケーションで使用されています。
特記のない限り、すべての画像は著者によるものです。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles

