「マスタリングモンテカルロ:より良い機械学習モデルをシミュレーションする方法」
マスタリングモンテカルロ:機械学習モデルのシミュレーション方法
確率的アプローチの応用によるシミュレーション技術を通じた予測アルゴリズムの強化

科学者がトランプで絶えず統計学のゲームを変えた方法
混乱の1945年、世界は第二次世界大戦の最後の苦悩に取り憑かれていましたが、ひっそりとソリティアのゲームが計算の領域で進歩を引き起こしました。これは普通のゲームではありませんが、モンテカルロ法(1)の誕生につながるものでした。プレイヤーは誰かと言えば、マンハッタン計画にも熱中していた科学者スタニスワフ・ウラムです(2)。ウラムは病気の回復中、ソリティアに没頭していました。ゲームの複雑な確率が彼を魅了し、ゲームを繰り返しシミュレーションすることでこれらの確率を良い近似値として提供できることに気付きました(3)。それは、フルーツではなくトランプカードを使ったニュートンのリンゴのような瞬間でした。ウラムはそのアイデアを同僚のジョン・フォン・ノイマンと共有し、彼らはモンテカルロ法を形式化しました。モンテカルロ法は、モナコの有名なカジノ「モンテカルロカジノ」(上記のエドヴァルド・ムンクの有名な絵画に描かれている)にちなんで名付けられ、高い賭け金と確率が支配する場所と同様、その手法自体も高い賭けとなります。
現代においては、モンテカルロ法は機械学習の世界で秘密兵器となり、強化学習、ベイジアンフィルタリング、複雑なモデルの最適化などのアプリケーションに活用されています(4)。その堅牢性と多様性により、その創始から70年以上経った現在でもその重要性が保たれています。ウラムのソリティアゲームから現代の洗練されたAIアプリケーションまで、モンテカルロ法は複雑なシステムに取り組むためのシミュレーションと近似の力を示すものです。
確率的シミュレーションでカードを正しくプレイする
データサイエンスと機械学習の複雑な世界では、モンテカルロシミュレーションは計算された賭けに似ています。この統計的手法により、不確実性の中で戦略的な賭けを行い、複雑で確定的な問題を確率的に解釈することができます。本記事では、モンテカルロシミュレーションを解説し、統計学と機械学習におけるその強力な応用を探求します。
まず、モンテカルロシミュレーションの理論について詳しく解説し、この手法が問題解決のための強力なツールとなる原則を明らかにします。その後、Pythonでの実践的なモンテカルロシミュレーションの実装を示しながら、いくつかのハンズオンアプリケーションを取り組みます。
- データモデリング入門、パート1:データモデリングとは何ですか?
- VoAGIニュース、8月2日:ChatGPTコードインタプリタ:高速データサイエンス•追いつけない?AIの今週の話題をキャッチアップしましょう
- ユーザーフィードバック – MLモニタリングスタックの欠けている部分
次に、モンテカルロシミュレーションを使用して機械学習モデルを最適化する方法について探求します。特に、ハイパーパラメータのチューニングという難しいタスクに焦点を当て、この複雑な領域をナビゲートするための実践的なツールキットを提供します。
では、賭けを行い、始めましょう!
モンテカルロシミュレーションの理解
モンテカルロシミュレーションは、数学者やデータサイエンティストにとって貴重な技術です。これらのシミュレーションは、広範で複雑な可能性の中を進むための方法論を提供し、教養のある仮定を立て、最適な解決策が導き出されるまで選択肢を徐々に洗練していきます。
その仕組みは次のとおりです。ある特定の事前定義されたプロセスに従って、大量のランダムなシナリオを生成し、これらのシナリオを検証してさまざまな結果の確率を推定します。これをより明確にするために、次の例え話を考えてみましょう。各シナリオを、人気のあるボードゲーム「クルー」のターンと考えます。「クルー」は、プレイヤーが犯罪の詳細を推理するために証拠を集めるという探偵スタイルのゲームです。各ターンや質問により、潜在的な答えが排除され、プレイヤーは真の犯罪シナリオを明らかにすることに近づいていきます。同様に、モンテカルロ研究の各シミュレーションは、複雑な問題の解決に向けて私たちをより近づける洞察を提供します。
機械学習の世界では、これらの「シナリオ」はさまざまなモデル構成、ハイパーパラメータの異なるセット、データセットをトレーニングセットとテストセットに分割する別の方法などを表すことができます。これらのシナリオの結果を評価することで、機械学習アルゴリズムの振る舞いについて有益な洞察を得ることができます。これにより、最適化に関する的確な意思決定が可能となります。
ダーツゲーム
モンテカルロシミュレーションを理解するために、ダーツゲームをしていると想像してみてください。ただし、特定のターゲットを狙うのではなく、目隠しをして大きな正方形のダーツボードにランダムにダーツを投げます。この正方形の中には円形のターゲットがあります。あなたの目標は、円の円周と直径の比であるπの値を推定することです。
不可能に思えるかもしれませんが、ここでのトリックは次のとおりです:円の面積と正方形の面積の比はπ/4です。したがって、たくさんのダーツを投げた場合、円の内部に着地したダーツの数を総ダーツ数で割った比率は、おおよそπ/4になるはずです。この比率に4を掛けると、πの推定値が得られます!
ランダムな推測とモンテカルロ
モンテカルロシミュレーションのパワーを示すために、よりシンプルな方法であるランダムな推測と比較してみましょう。
以下のコードを両方の場合(ランダムとモンテカルロ)で実行すると、毎回異なる予測結果が得られます。これはダーツがランダムに投げられるため、予想されることです。これはモンテカルロシミュレーションの主な特徴です:それらは本質的に確率的またはランダムです。しかし、このランダム性にもかかわらず、適切に使用すれば非常に正確な推定値を提供することができます。したがって、あなたの図は私のものとまったく同じには見えませんが、同じストーリーを伝えます。
最初の一連の可視化(図1aから図1f)では、piの値について一連のランダムな推測を行い、各推測に基づいて円を生成しています。この「ランダム性」を正しい方向にプッシュし、piの正確な値を覚えていないかもしれないが、2より大きく4より小さいことを仮定します。結果の図からわかるように、円のサイズは推測に応じて大きく変動し、このアプローチの不正確さを示しています(これは驚くべきことではありません)。各図の青い円はランダムな推測に基づいています。
#Piのランダムな推測# このコードを実行する前に、必要なパッケージがインストールされていることを確認してください。# ターミナルで「pip install」を使用するか、conda環境を使用している場合は「conda install」を使ってインストールできます。# 必要なライブラリをインポートimport randomimport plotly.graph_objects as goimport numpy as np# 推測の回数を設定します。より多くの推測とその後のプロットのためにこれを調整してくださいnum_guesses = 6# ユニットサークルの座標を生成します。# np.linspaceを使用して、0から2*piまでの範囲で均等に分布した数値を生成します。# これらはユニットサークル内の角度を表します。theta = np.linspace(0, 2*np.pi, 100)# ユニットサークルのx座標とy座標は、それぞれこれらの角度の余弦と正弦です。unit_circle_x = np.cos(theta)unit_circle_y = np.sin(theta)# piの値についていくつかの推測を行います。for i in range(num_guesses): # 2から4の範囲でpiのランダムな推測を行います。 pi_guess = random.uniform(2, 4) # 推測に基づいて円の座標を生成します。 # 円の半径はpiの推測値を4で割ったものです。 radius = pi_guess / 4 # 円のx座標とy座標は、それぞれ半径に角度の余弦と正弦を掛けたものです。 circle_x = radius * np.cos(theta) circle_y = radius * np.sin(theta) # 円の散布図を作成します。 fig = go.Figure() # プロットに円を追加します。 # 円を描画するために、モードが'lines'のScatterトレースを使用します。 fig.add_trace(go.Scatter( x = circle_x, y = circle_y, mode='lines', line=dict( color='blue', width=3 ), name='推定された円' )) # プロットにユニットサークルを追加します。 fig.add_trace(go.Scatter( x = unit_circle_x, y = unit_circle_y, mode='lines', line=dict( color='green', width=3 ), name='ユニットサークル' )) # プロットのレイアウトを更新します。 # タイトルにpiの推測値を含め、円を適切に表示するためにサイズと軸の範囲を調整します。 fig.update_layout( title=f"Fig1{chr(97 + i)}: Piのランダムな推測: {pi_guess}", width=600, height=600, xaxis=dict( constrain="domain", range=[-1, 1] ), yaxis=dict( scaleanchor="x", scaleratio=1, range=[-1, 1] ) ) # プロットを表示します。 fig.show()
何か変わった点に気づくかもしれません。ランダムな推測法では、時には円周の推定値に近い推測が単位円から遠く離れた円になることがあります。この矛盾は、円周を見ているためであり、半径や面積ではなく、円の円周を推定した際の誤差を表しています。2つの円の間の視覚的なギャップは、円全体ではなく、推測に基づいた円周の推定誤差を表しています。
2番目の視覚化セット(図2aから図2f)では、モンテカルロ法を使用して円周率の値を推定しています。ランダムな推測を行う代わりに、正方形に大量のダーツを投げ、正方形に内接する円の内部に落ちたダーツの数を数えます。結果として得られる円のサイズは、実際の単位円に非常に近くなるため、より正確な推定値となります。緑色の点は単位円の内部に着地したダーツを、赤色の点は外部に着地したダーツを表しています。
#円周率のモンテカルロ推定# 必要なライブラリをインポートimport randomimport mathimport plotly.graph_objects as goimport plotly.io as pioimport numpy as np# ダーツを投げて円周率を推定します。10,000個のダーツを投げましょう。num_darts = 10000# 円の内部に着地したダーツを追跡するために変数を用意します。darts_in_circle = 0# 円の内部および外部に落ちたダーツの座標を保存します。x_coords_in, y_coords_in, x_coords_out, y_coords_out = [], [], [], []# シミュレーション中に6つの図を生成します。したがって、1,666回のダーツごとに新しい図を作成します(10,000を6で割った数)。num_figures = 6darts_per_figure = num_darts // num_figures# 真の単位円と比較するために単位円を作成します。ここでは極座標を使用し、直交座標に変換します。theta = np.linspace(0, 2*np.pi, 100)unit_circle_x = np.cos(theta)unit_circle_y = np.sin(theta)# ダーツを投げ始めます(1x1の正方形内のランダムな点をシミュレートし、それが四分円の内部に落ちるかどうかを確認します)。for i in range(num_darts): # -1から1の範囲でランダムなx、y座標を生成します。 x, y = random.uniform(-1, 1), random.uniform(-1, 1) # ダーツ(点)が原点(0,0)よりも距離1未満に近い場合、それは円の内部にあります。 if math.sqrt(x**2 + y**2) <= 1: darts_in_circle += 1 x_coords_in.append(x) y_coords_in.append(y) else: x_coords_out.append(x) y_coords_out.append(y) # 各1,666回のダーツごとに、推定値が真の単位円と比較した場合の見た目を確認します。 if (i + 1) % darts_per_figure == 0: # ダーツが円の内部に着地した割合(総ダーツ数に対する円の内部に着地したダーツの割合)を使用して円周率を推定します。 pi_estimate = 4 * darts_in_circle / (i + 1) # 現在の推定値から円を作成し、単位円と比較します。 estimated_circle_radius = pi_estimate / 4 estimated_circle_x = estimated_circle_radius * np.cos(theta) estimated_circle_y = estimated_circle_radius * np.sin(theta) # Plotlyを使用して結果をプロットします。 fig = go.Figure() # 円の内部および外部に着地したダーツをプロットに追加します。 fig.add_trace(go.Scattergl(x=x_coords_in, y=y_coords_in, mode='markers', name='円の内部に着地したダーツ', marker=dict(color='green', size=4, opacity=0.8))) fig.add_trace(go.Scattergl(x=x_coords_out, y=y_coords_out, mode='markers', name='円の外部に着地したダーツ', marker=dict(color='red', size=4, opacity=0.8))) # 真の単位円と推定された円をプロットに追加します。 fig.add_trace(go.Scatter(x=unit_circle_x, y=unit_circle_y, mode='lines', name='単位円', line=dict(color='green', width=3))) fig.add_trace(go.Scatter(x=estimated_circle_x, y=estimated_circle_y, mode='lines', name='推定された円', line=dict(color='blue', width=3))) # プロットのレイアウトをカスタマイズします。 fig.update_layout(title=f"図{chr(97 + (i + 1) // darts_per_figure - 1)}:投げられたダーツ:{(i + 1)}、推定された円周率:{pi_estimate}", width=600, height=600, xaxis=dict(constrain="domain", range=[-1, 1]), yaxis=dict(scaleanchor="x", scaleratio=1, range=[-1, 1]), legend=dict(yanchor="top", y=0.99, xanchor="left", x=0.01)) # プロットを表示します。 fig.show() # プロットをPNGイメージファイルとして保存します。 pio.write_image(fig, f"fig2{chr(97 + (i + 1) // darts_per_figure - 1)}.png")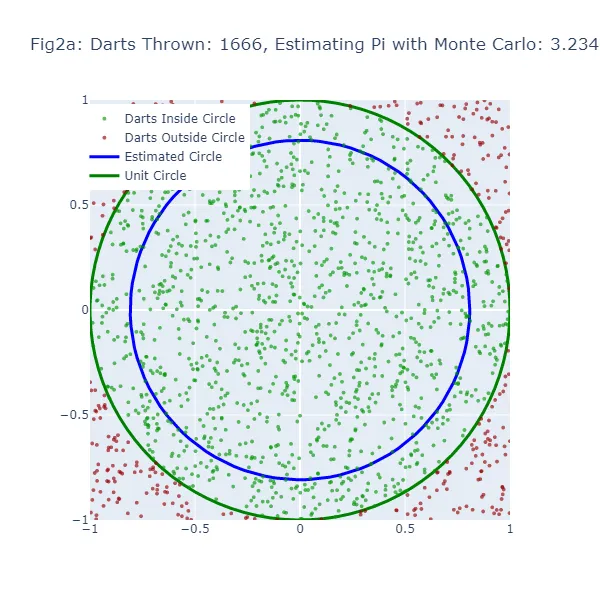
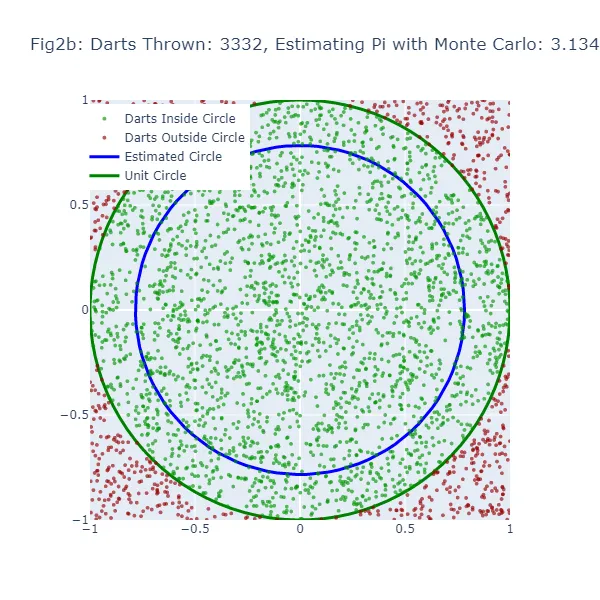
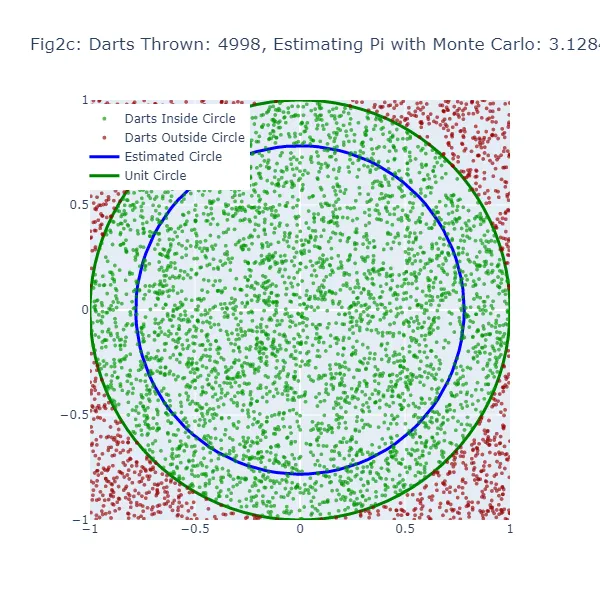
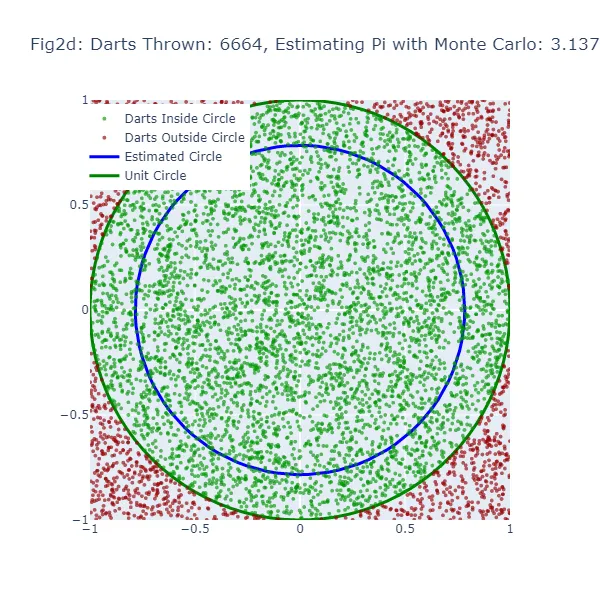
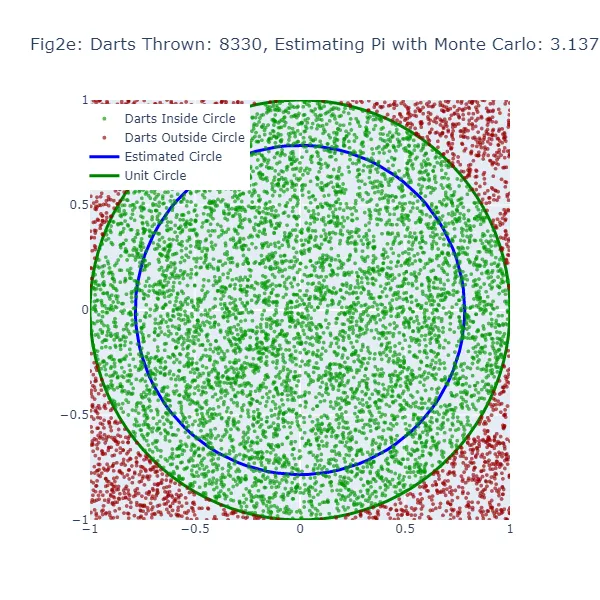

モンテカルロ法では、円の内部に落ちる「ダーツ」の割合を全ての投げられたダーツの数で割ったものが円周率の推定値になります。推定された円周率の値を使って円を描画します。モンテカルロ推定が不正確な場合、円の大きさも間違ってしまいます。この推定された円と単位円の間の隙間の幅は、モンテカルロ推定の精度を示すものです。
しかし、モンテカルロ法では「ダーツ」の数が増えるほど、より正確な推定値を生成するため、推定された円はより多くの「ダーツ」が投げられるにつれて単位円に収束するはずです。したがって、両方の方法でも推定が不正確な場合に隙間が表示されますが、「ダーツ」の数が増えるにつれてモンテカルロ法の方が一貫して隙間が減少するはずです。
円周率の予測:確率の力
モンテカルロシミュレーションの威力は、ランダム性を利用して確定的な問題を解決する能力にあります。大量のランダムなシナリオを生成し、その結果を分析することで、解析的に解くのが難しい複雑な問題の確率を推定することができます。
円周率の推定においては、モンテカルロ法を使ってランダムにダーツを投げるだけで非常に正確な推定値を得ることができます。先述の通り、ダーツを投げる回数が増えるほど、推定値はより正確になります。これは大数の法則と呼ばれるもので、大量の試行から得られた結果の平均値は期待値に近くなるという確率論の基本的な概念であり、試行回数が増えるにつれてより一貫して近づく傾向があります。図2a-2fで示される6つの例について、投げられたダーツの数とモンテカルロ推定された円周率と実際の円周率の差をプロットして、これが真実に近づくかどうかを見てみましょう。一般的には、私たちのグラフ(図2g)は負の傾向を示すはずです。これを実現するためのコードは以下の通りです:
# Calculate the differences between the real pi and the estimated pidiff_pi = [abs(estimate - math.pi) for estimate in pi_estimates]# Create the figure for the number of darts vs difference in pi plot (Figure 2g)fig2g = go.Figure(data=go.Scatter(x=num_darts_thrown, y=diff_pi, mode='lines'))# Add title and labels to the plotfig2g.update_layout( title="Fig2g: Darts Thrown vs Difference in Estimated Pi", xaxis_title="Number of Darts Thrown", yaxis_title="Difference in Pi",)# Display the plotfig2g.show()# Save the plot as a pngpio.write_image(fig2g, "fig2g.png")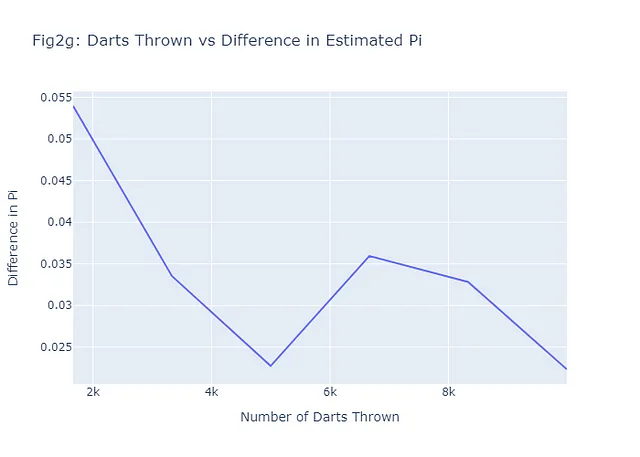
たった6つの例であっても、一般的なパターンは予想通りです。ダーツをより多く投げる(より多くのシナリオ)、推定値と実際の値との間の差が小さくなり、より良い予測ができます。
1,000,000回の総ダーツを投げ、500回の予測を許可しましょう。言い換えれば、1,000,000回のダーツ投げのシミュレーション中に均等に間隔をあけて500回の予測されたpi値と実際のpi値の差を記録します。500個の追加の図を生成する代わりに、私たちが確認しようとしている内容に進むことにしましょう:ダーツを投げる回数が増えるにつれて、予測されたpi値と実際のpi値の差が小さくなるかどうか、これが本当に真実であるかどうかです。散布図(図2h)を使用します:
#500モンテカルロシナリオ;1,000,000回のダーツを投げるimport randomimport mathimport plotly.graph_objects as goimport numpy as np# 投げるダーツの総数(1M)num_darts = 1000000darts_in_circle = 0# 記録するシナリオの数(500)num_scenarios = 500darts_per_scenario = num_darts // num_scenarios# 各シナリオのデータを保存するためのリストdarts_thrown_list = []pi_diff_list = []# 一定数のダーツを投げるfor i in range(num_darts): # -1から1までのランダムなx、y座標を生成 x, y = random.uniform(-1, 1), random.uniform(-1, 1) # ダーツが円の内部にあるかどうかをチェック # ダーツは、原点(0,0)からの距離が1以下の場合、円の内部にあると言える if math.sqrt(x**2 + y**2) <= 1: darts_in_circle += 1 # シナリオを記録するタイミングである場合 if (i + 1) % darts_per_scenario == 0: # モンテカルロ法でpi値を推定する # 推定値は円の内部にあるダーツの数を総ダーツの数で割ったものに4を掛けたもの pi_estimate = 4 * darts_in_circle / (i + 1) # 投げられたダーツの数と推定値と実際のpi値の差を記録する darts_thrown_list.append((i + 1) / 1000) # 1000で割って表示を千単位で行うため pi_diff_list.append(abs(pi_estimate - math.pi))# データの散布図を作成するfig = go.Figure(data=go.Scattergl(x=darts_thrown_list, y=pi_diff_list, mode='markers'))# プロットのレイアウトを更新するfig.update_layout( title="図2h: 推定pi値と実際のpi値の差 vs. 投げたダーツの数(千単位)", xaxis_title="投げたダーツの数(千単位)", yaxis_title="推定pi値と実際のpi値の差",)# プロットを表示するfig.show()# プロットをpngとして保存するpio.write_image(fig2h, "fig2h.png")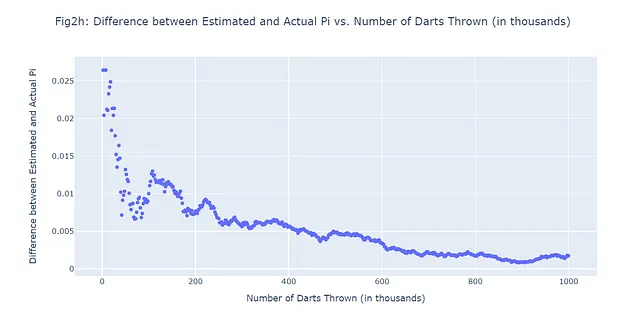
モンテカルロシミュレーションとハイパーパラメータのチューニング:成功の組み合わせ
この時点で、あなた自身に思っているかもしれません。「モンテカルロは興味深い統計ツールですが、機械学習にどのように適用されるのでしょうか?」短い答えは:多くの方法で適用されます。モンテカルロシミュレーションの機械学習における多くの応用の1つは、ハイパーパラメータのチューニングの領域です。
ハイパーパラメータは、機械学習アルゴリズムを設定する際に私たち(人間)が調整するつまみやダイヤルです。これらは、データから学習されないアルゴリズムの振る舞いを制御します。例えば、決定木では、木の最大深さはハイパーパラメータです。ニューラルネットワークでは、学習率と隠れ層の数がハイパーパラメータです。
適切なハイパーパラメータを選ぶことは、性能が悪いモデルと優れたモデルの違いを生み出すことができます。しかし、どのハイパーパラメータを選ぶべきか、どのように知るのでしょうか?これがモンテカルロシミュレーションの出番です。
従来、機械学習の実践者は、グリッドサーチやランダムサーチなどの方法を使用してハイパーパラメータをチューニングしてきました。これらの方法は、各ハイパーパラメータの可能な値のセットを指定し、ハイパーパラメータのすべての組み合わせに対してモデルをトレーニングし評価することを含みます。これは、チューニングするハイパーパラメータの数が多い場合や、各ハイパーパラメータが取り得る可能な値の範囲が広い場合に、計算量が多く時間がかかることがあります。
モンテカルロシミュレーションは、より効率的な代替手段を提供します。ハイパーパラメータのすべての組み合わせを徹底的に調べる代わりに、確率分布に従ってハイパーパラメータの空間からランダムにサンプリングすることができます。これにより、ハイパーパラメータ空間を効率的に探索し、良いハイパーパラメータの組み合わせをより速く見つけることができます。
次のセクションでは、実際のデータセットを使用して、モンテカルロシミュレーションを実践的なハイパーパラメータチューニングにどのように使用するかを示します。では、始めましょう!
ハイパーパラメータチューニングのためのモンテカルロシミュレーション
実験の鼓動:心臓病データセット
機械学習の世界では、データはモデルのエンジンとなる命であります。モンテカルロシミュレーションを用いたハイパーパラメータチューニングの探索では、心臓に近いデータセットを見てみましょう。UCI Machine Learning RepositoryのHeart Diseaseデータセット(CC BY 4.0)は、心臓病を持つ患者の医療記録のコレクションです。
このデータセットには、年齢、性別、胸痛のタイプ、安静時血圧、コレステロールレベル、空腹時血糖値などを含む14の属性があります。ターゲット変数は心臓病の存在であり、これはバイナリ分類のタスクです。カテゴリカルと数値の特徴の組み合わせであり、ハイパーパラメータチューニングのデモンストレーションには興味深いデータセットです。
まず、作業内容を把握するためにデータセットを見てみましょう。
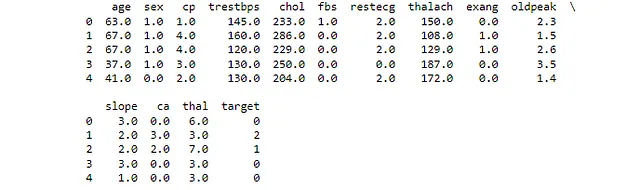
#データセットの最初の数行を読み込みます# 必要なライブラリをインポートしますimport pandas as pdfrom sklearn.model_selection import train_test_splitfrom sklearn.preprocessing import StandardScaler, OneHotEncoderfrom sklearn.compose import ColumnTransformerfrom sklearn.pipeline import Pipelinefrom sklearn.linear_model import LogisticRegressionfrom sklearn.model_selection import GridSearchCVfrom sklearn.metrics import roc_auc_scoreimport numpy as npimport plotly.graph_objects as go# データセットを読み込みます# データセットはUCI Machine Learning Repositoryで利用可能です# これは心臓病に関するデータセットで患者のさまざまな測定値を含んでいますurl = "https://archive.ics.uci.edu/ml/machine-learning-databases/heart-disease/processed.cleveland.data"# データフレームの列名を定義します# pandasに'?'をNaNとして扱うように指定しますcolumn_names = ["age", "sex", "cp", "trestbps", "chol", "fbs", "restecg", "thalach", "exang", "oldpeak", "slope", "ca", "thal", "target"]# データセットをpandasのデータフレームに読み込みます# 列名を指定し、pandasに'?'をNaNとして扱うように指定しますdf = pd.read_csv(url, names=column_names, na_values="?")# データフレームの最初の数行を表示します# これによりデータの概要がすばやくわかりますprint(df.head())これにより、すべての列におけるデータセットの最初の4つの値が表示されます。正しいCSVを読み込み、列名を指定した場合、出力は図3のようになります。
パルスの設定:データの前処理
ハイパーパラメータチューニングにHeart Diseaseデータセットを使用する前に、データを前処理する必要があります。これには以下の手順が含まれます:
- 欠損値の処理:データセットの一部のレコードには欠損値があります。これらを削除するか、欠損値を埋めるか、他の方法で処理する必要があります。
- カテゴリ変数のエンコーディング:多くの機械学習アルゴリズムは、入力データが数値である必要があります。カテゴリ変数を数値形式に変換する必要があります。
- 数値特徴の正規化:数値特徴が同じスケールにあると、多くの機械学習アルゴリズムのパフォーマンスが向上します。これらの特徴のスケールを調整するために正規化を適用します。
まず、欠損値の処理から始めましょう。Heart Diseaseデータセットでは、「ca」と「thal」という列にいくつかの欠損値があります。これらの欠損値をそれぞれの列の中央値で埋めます。これは欠損データの処理に一般的な戦略であり、データの分布に大きな影響を与えません。
次に、カテゴリ変数をエンコードします。データセットでは、「cp」、「restecg」、「slope」、「ca」、「thal」という列がカテゴリ変数です。ラベルエンコーディングを使用して、これらのカテゴリ変数を数値に変換します。ラベルエンコーディングでは、列内の各ユニークなカテゴリに異なる整数を割り当てます。
最後に、数値特徴を正規化します。正規化は、数値特徴のスケールを調整して、すべてが同じ範囲に収まるようにします。これは多くの機械学習アルゴリズムのパフォーマンスを改善するのに役立ちます。正規化には標準化を使用し、データの平均が0、標準偏差が1になるように変換します。
以下は、これらの前処理手順を実行するPythonコードです:
# Preprocess
# 必要なライブラリをインポート
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import LabelEncoder
# データセット内の欠損値を特定
# これにより、各列の欠損値の数が表示されます
print(df.isnull().sum())
# 欠損値を列の中央値で埋める
# sklearnのSimpleImputerクラスは、欠損値を埋めるための基本的な戦略を提供します
# 'median'戦略を使用しており、欠損値を各列の中央値で置き換えています
imputer = SimpleImputer(strategy='median')
# データフレームにimputerを適用
# 結果は、欠損値が埋められた新しいデータフレームです
df_filled = pd.DataFrame(imputer.fit_transform(df), columns=df.columns)
# 埋められたデータフレームの最初の数行を表示
# これにより、埋め込みが正しく行われたことを簡単に確認できます
print(df_filled.head())
# データセット内のカテゴリ変数を特定
# これらは、非数値データを含む変数です
categorical_vars = df_filled.select_dtypes(include='object').columns
# カテゴリ変数をエンコード
# sklearnのLabelEncoderクラスは、各一意の文字列を一意の整数に変換します
encoder = LabelEncoder()
for var in categorical_vars:
df_filled[var] = encoder.fit_transform(df_filled[var])
# 数値特徴量を正規化
# sklearnのStandardScalerクラスは、平均を除去し、単位分散にスケーリングすることにより特徴量を標準化します
scaler = StandardScaler()
# データフレームにスケーラーを適用
# 結果は、数値特徴量が正規化された新しいデータフレームです
df_normalized = pd.DataFrame(scaler.fit_transform(df_filled), columns=df_filled.columns)
# 正規化されたデータフレームの最初の数行を表示
# これにより、正規化が正しく行われたことを簡単に確認できます
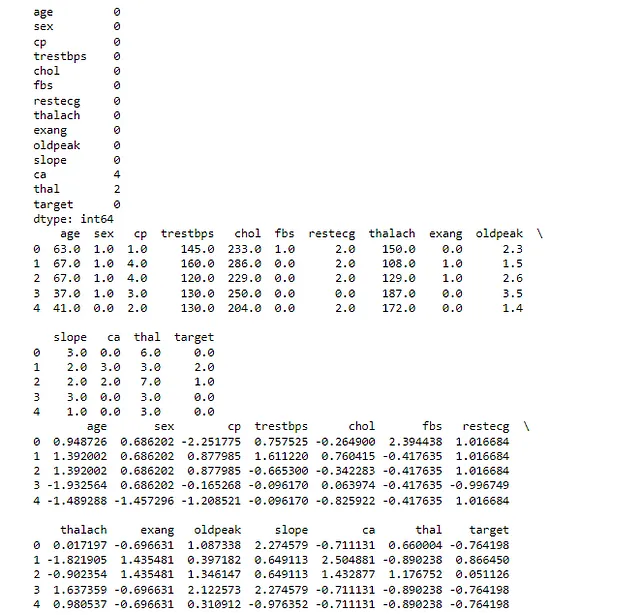
print(df_normalized.head())最初のprint文は、元のデータセットの各列における欠損値の数を示しています。この場合、’ca’と’thal’の列にはいくつかの欠損値がありました。
2番目のprint文は、欠損値を埋めた後のデータセットの最初の数行を示しています。前述のように、各列の中央値を使って欠損値を埋めました。
3番目のprint文は、カテゴリ変数をエンコードした後のデータセットの最初の数行を示しています。このステップの後、データセット内のすべての変数が数値になります。
最後のprint文は、数値特徴量を正規化した後のデータセットの最初の数行を示しています。このステップの後、データセット内のすべての数値特徴量は同じスケールになります。出力が図4に似ているか確認してください:
このコードを実行すると、モデリングに適した前処理済みのデータセットが得られます。
基本的な機械学習モデルの実装
データの前処理が完了したので、基本的な機械学習モデルを実装する準備が整いました。これは私たちのベースラインモデルとなります。後でハイパーパラメータのチューニングを通じて改善を試みます。
このタスクでは、シンプルなロジスティック回帰モデルを使用します。注意点として、「回帰」と呼ばれていますが、これは実際にはバイナリ分類問題(Heart Diseaseデータセットで扱っているものと同様)の最もポピュラーなアルゴリズムの1つです。これは、正例の確率を予測する線形モデルです。
モデルのトレーニング後、一般的な指標である正解率とROC-AUCでモデルのパフォーマンスを評価します。正解率は、すべての予測のうち正しい予測の割合であり、ROC-AUC(受信者動作特性 – 曲線下面積)は真陽性率と偽陽性率のトレードオフを測定します。
では、新たに前処理されたデータに基づいて基本的なロジスティック回帰モデルを実装し、評価するPythonコードを示します:
# Logistic Regression Model - Baseline
# 必要なライブラリをインポート
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, roc_auc_score
# 正規化されたDataFrame内の'target'列を元の'target'列で置き換える
# これは、'target'列も正規化されているため、望ましくない操作です
df_normalized['target'] = df['target']
# 'target'列を2値化する
# 元の'target'列には0から4までの値が含まれています
# 問題を心臓病の有無の2値分類問題に単純化します
df_normalized['target'] = df_normalized['target'].apply(lambda x: 1 if x > 0 else 0)
# データをトレーニングセットとテストセットに分割
# 'target'列はラベルなので、特徴量(X)から削除します
# テストサイズは20%で、データの80%がトレーニングに使用され、20%がテストに使用されるように設定します
X = df_normalized.drop('target', axis=1)
y = df_normalized['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 基本的なロジスティック回帰モデルを実装
# ロジスティック回帰は、バイナリ分類問題に適したシンプルでパワフルな線形モデルです
model = LogisticRegression()
model.fit(X_train, y_train)
# テストセット上で予測を行う
# モデルはトレーニング済みなので、未知のデータで予測に使用できます
y_pred = model.predict(X_test)
# モデルを評価する
# 正解率(正しい予測の割合)とROC-AUC(モデルがクラスを区別する能力を測定する指標)を使用します
accuracy = accuracy_score(y_test, y_pred)
roc_auc = roc_auc_score(y_test, y_pred)
# パフォーマンスメトリクスを表示する
# これにより、モデルのパフォーマンスを把握することができます
print("ベースラインモデル " + f'正解率: {accuracy}')
print("ベースラインモデル " + f'ROC-AUC: {roc_auc}')
精度0.885、ROC-AUCスコア0.884で、基本的なロジスティック回帰モデルは改善のための堅固なベースラインを確立しました。これらのメトリクスは、当社のモデルが心臓病のある患者とない患者を区別するのに非常に優れていることを示しています。さて、さらに良くすることができるか見てみましょう。
グリッドサーチによるハイパーパラメータのチューニング
機械学習では、モデルのパフォーマンスをハイパーパラメータのチューニングによって改善することがよくあります。ハイパーパラメータとは、データから学習されないパラメータであり、学習プロセスの開始前に設定されます。例えば、ロジスティック回帰では、正則化の強さの「C」とペナルティの種類の「l1」または「l2」がハイパーパラメータです。
グリッドサーチを使用してロジスティック回帰モデルのハイパーパラメータチューニングを行いましょう。ハイパーパラメータの「C」と「ペナルティ」をチューニングし、スコアリングメトリックとしてROC-AUCを使用します。ベースラインモデルのパフォーマンスを上回ることができるか見てみましょう。
さて、このセクションのPythonコードから始めましょう。
# グリッドサーチ# 必要なライブラリをインポートfrom sklearn.model_selection import GridSearchCV# ハイパーパラメータとその値を定義する# 'C'は正則化強度の逆数(小さい値は強い正則化を指定する)# 'penalty'は罰則のノルムを指定する(l1またはl2)hyperparameters = {'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000], 'penalty': ['l1', 'l2']}# グリッドサーチを実装する# GridSearchCVはモデルのハイパーパラメータをチューニングするためのメソッドです# モデル、チューニングするハイパーパラメータ、クロスバリデーションのためのフォールド数を渡します# スコアリングメトリックとしてROC-AUCを使用していますgrid_search = GridSearchCV(LogisticRegression(), hyperparameters, cv=5, scoring='roc_auc')grid_search.fit(X_train, y_train)# 最適なハイパーパラメータを取得する# GridSearchCVはモデルの最適なハイパーパラメータを見つけたので、それを出力しますbest_params = grid_search.best_params_print(f'最適なハイパーパラメータ: {best_params}')# 最適なモデルを評価する# GridSearchCVはまた、最適なモデルを提供してくれるので、予測を行いパフォーマンスを評価できますbest_model = grid_search.best_estimator_y_pred_best = best_model.predict(X_test)accuracy_best = accuracy_score(y_test, y_pred_best)roc_auc_best = roc_auc_score(y_test, y_pred_best)# 最適なモデルのパフォーマンスメトリクスを出力する# これらは、ハイパーパラメータチューニング後のモデルのパフォーマンスを示していますprint("グリッドサーチメソッド " + f'最適なモデルの精度: {accuracy_best}')print("グリッドサーチメソッド " + f'最適なモデルのROC-AUC: {roc_auc_best}')
最適なハイパーパラメータが{‘C’: 0.1, ‘penalty’: ‘l2’}となり、グリッドサーチによる最良モデルの精度は0.852、ROC-AUCスコアは0.853です。興味深いことに、このパフォーマンスはベースラインモデルよりもわずかに低いです。これは、ベースラインモデルのハイパーパラメータがこの特定のデータセットに既に適していたためか、トレインテスト分割のランダム性の結果かもしれません。いずれにしても、より複雑なモデルやテクニックが常に良いわけではないということを思い出す貴重な機会です。
ただし、グリッドサーチが探索したハイパーパラメータの組み合わせは比較的少ないことに気付いたかもしれません。実際には、ハイパーパラメータの数とその潜在的な値ははるかに大きくなる場合があり、グリッドサーチは計算コストが高く、実行不可能であることさえあります。
ここでモンテカルロ法が登場します。このよりガイドされたアプローチが、元のベースラインモデルまたはグリッドサーチベースのモデルのパフォーマンスを向上させるかどうかを見てみましょう。
#モンテカルロ# 必要なライブラリをインポートfrom sklearn.metrics import accuracy_score, roc_auc_scorefrom sklearn.linear_model import LogisticRegressionfrom sklearn.model_selection import train_test_splitimport numpy as np# データをトレーニングセットとテストセットに分割するX_train、X_test、y_train、y_test = train_test_split(X、y、test_size=0.2、random_state=42)# ハイパーパラメータの範囲を定義する# 'C'は正則化強度の逆数(小さい値は強い正則化を指定する)# 'penalty'は罰則のノルムを指定する(l1またはl2)C_range = np.logspace(-3、3、7)penalty_options = ['l1'、'l2']# 最良のスコアとハイパーパラメータを格納する変数を初期化するbest_score = 0best_hyperparams = None# モンテカルロシミュレーションを実行する# 1000回の反復を実行します。この数を変更してパフォーマンスがどのように変化するかを確認できます。# 大数の法則を覚えておいてください!for _ in range(1000): # ハイパーパラメータを定義された範囲からランダムに選択 C = np.random.choice(C_range) penalty = np.random.choice(penalty_options) # これらのハイパーパラメータでモデルを作成し評価する # 'liblinear'ソルバーを使用しているため、L1とL2の両方の正則化をサポートしています model = LogisticRegression(C=C, penalty=penalty, solver='liblinear') model.fit(X_train, y_train) y_pred = model.predict(X_test) # 精度とROC-AUCを計算する accuracy = accuracy_score(y_test, y_pred) roc_auc = roc_auc_score(y_test, y_pred) # これまでのモデルのROC-AUCが最も良い場合、そのスコアとハイパーパラメータを格納する if roc_auc > best_score: best_score = roc_auc best_hyperparams = {'C': C, 'penalty': penalty}# 最良のスコアとハイパーパラメータを出力するprint("モンテカルロ法 " + f'最良のROC-AUC: {best_score}')print("モンテカルロ法 " + f'最良のハイパーパラメータ: {best_hyperparams}')# 最良のハイパーパラメータでモデルをトレーニングするbest_model = LogisticRegression(**best_hyperparams, solver='liblinear')best_model.fit(X_train, y_train)# テストセットでの予測を行うy_pred = best_model.predict(X_test)# 最良のモデルの精度を計算して出力するaccuracy = accuracy_score(y_test, y_pred)print("モンテカルロ法 " + f'最良のモデルの精度

モンテカルロ法では、最も優れたROC-AUCスコアは0.9014であり、最良のハイパーパラメータは{‘C’: 0.1, ‘penalty’: ‘l1’}でした。最良モデルの正確性は0.9016でした。
モンテカルロはまさにデッキからエースを引き当てたようです - これはベースラインモデルとグリッドサーチを使用して調整されたモデルの両方よりも改善されています。Pythonコードを調整してパフォーマンスに影響を与えるかどうかを確認することをお勧めします。ハイパーパラメータスペースを増やしてグリッドサーチ法を改善したり、計算時間をモンテカルロ法と比較したりしてみてください。モンテカルロ法の反復回数を増減させることでパフォーマンスにどのような影響を与えるかを確認してください。
結論
モンテカルロ法は、ソリティアのゲームから生まれたものであり、計算数学とデータサイエンスの景観を確かに変えました。その力は、その単純さと多目的性にあり、比較的簡単に複雑な高次元の問題に取り組むことができます。ダーツゲームで円周率の値を推定することから、機械学習モデルのハイパーパラメータの調整まで、モンテカルロシミュレーションは私たちのデータサイエンスの武器庫で貴重なツールであることが証明されています。
この記事では、モンテカルロ法の起源から理論的な基礎、機械学習への実践的な応用までを旅しました。実世界のデータセットを使用してハイパーパラメータのチューニングを行い、機械学習モデルの最適化に使用する方法を実践的に探求しました。また、他の方法と比較してその効率性と効果を示しました。
しかし、モンテカルロの物語はまだ終わっていません。機械学習とデータサイエンスの限界を押し広げるにつれて、モンテカルロ法は間違いなく重要な役割を果たし続けるでしょう。洗練されたAIアプリケーションを開発したり、複雑なデータを理解したり、単にソリティアのゲームをプレイしたりする場合でも、モンテカルロ法はシミュレーションと近似の力を通じて複雑な問題を解決する能力の証です。
これからも、この方法の美しさに一瞬立ち止まり、シンプルなカードゲームに根付いた方法が世界で最も高度な計算を推進する力について感謝しましょう。モンテカルロ法は確かに高賭けの運と複雑さのゲームであり、これまでのところ、常に勝利しているようです。だから、デッキをシャッフルし続け、カードをプレイし続け、そして覚えておいてください - データサイエンスのゲームでは、モンテカルロ法があなたの穴のエースになるかもしれません。
まとめ
おめでとうございます!最後までたどり着きました!確率の世界に没頭し、複雑なモデルに取り組み、モンテカルロシミュレーションの力に対する新たな感謝を手に入れました。それらが実際に動作する様子を見ました。複雑な問題を管理可能なコンポーネントに単純化し、機械学習タスクのハイパーパラメータを最適化することさえも。
私と同じようにMLの問題解決の微妙な点に没頭することが好きなら、VoAGIとLinkedInでフォローしてください。一緒にAIの迷宮を進む、賢明な解決策を一つずつ探求しましょう。
次の統計的冒険まで、探求し続け、学び続け、シミュレーションし続けましょう!そして、データサイエンスと機械学習の旅で、運が常にあなたの味方であることを祈っています。
注:すべての画像は、特に記載がない限り、著者によるものです。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
