バイナリおよびマルチクラスのターゲット変数のためのSHAP

バイナリおよびマルチクラスのSHAP

カテゴリカルな目標変数を予測するモデルのコードとSHAPプロットの解釈に関するガイド

SHAP値は、モデルの特徴量が予測に対してどのような貢献をしているかを示します。2値の目標変数の場合、これらの値は対数オッズとして解釈します。マルチクラスの目標変数の場合、softmaxを使用します。以下の作業を行います。

• これらの解釈について詳しく説明する
• SHAPプロットを表示するためのコードを提供する
• マルチクラスの目標変数に対してSHAP値を集計する新しい方法を探る

また、このトピックに関するビデオもご覧いただけます。

前回のSHAPチュートリアル

前回のSHAPチュートリアルから続けます。連続的な目標変数に対するSHAPプロットについて詳しく説明します。これらのプロットとその洞察は、カテゴリカルな目標変数に対しても同様です。GitHubで完全なプロジェクトも見つけることができます。

PythonでのSHAPの紹介

SHAPプロットの作成と解釈方法：ウォーターフォール、フォース、平均SHAP、ビースワーム、依存関係

towardsdatascience.com

• GGMLとllama.cppを使用してLlamaモデルを量子化する
• エントロピーを使用した時系列複雑性解析
• 機械学習プロジェクトのロードマップの設計方法

要約すると、SHAPを使用してアワビデータセットを使用して構築したモデルを説明しました。データセットには4,177のインスタンスがあり、以下に特徴量の例を示します。私たちは8つの特徴量を使用してy（アワビの殻にあるリングの数）を予測します。リングはアワビの年齢に関連しています。このチュートリアルでは、yを異なるグループに分割して2値およびマルチクラスの目標変数を作成します。

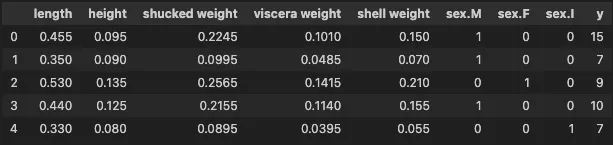
2値の目標変数

連続的な目標変数の場合、各インスタンスには8つのSHAP値があります。図1に示すように、これらを合計し、平均予測E[f(x)]と合わせると、そのインスタンスの予測f(x)が得られます。2値の目標変数の場合も同じ性質がありますが、値を正の予測の対数オッズとして解釈します。

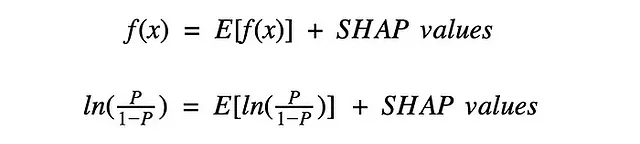
これを理解するために、SHAPプロットに入ってみましょう。まず、2値の目標変数を作成します（行2）。yに基づいて2つのグループを作成します：

• アワビのリングの数が平均以上の場合は1
• それ以外の場合は0

#2値の目標変数の作成y_bin = [1 if y_>10 else 0 for y_ in y]

この目標変数と8つの特徴量を使用してXGBoost分類器を訓練します（行2-3）。このモデルの精度は96.6%でした。

#モデルの訓練model_bin = xgb.XGBClassifier(objective="binary:logistic")model_bin.fit(X, y_bin)

次にSHAP値を計算します（行2-3）。このオブジェクトの形状を出力します（行5）、これは(4177, 8)を示します。したがって、連続的な目標変数と同様に、1つの予測と特徴量ごとに1つのSHAP値があります。後で、マルチクラスの目標変数についてはこれがどのように異なるかを見ていきます。

# SHAP値を取得
explainer = shap.Explainer(model_bin)
shap_values_bin = explainer(X)
print(shap_values_bin.shape) #出力: (4177, 8)

最初のインスタンスに対してウォーターフォールプロットを表示します（行6）。結果は図2で確認できます。コードは連続変数の場合と同じです。数値以外は、ウォーターフォールプロットも似ています。

# 最初のインスタンスに対するウォーターフォールプロット
shap.plots.waterfall(shap_values_bin[0])

今、E[f(x)] = -0.789は4,177個のアワビ全体での平均予測対数オッズを表します。つまり、陽性（1）の予測の対数オッズです。この特定のアワビについて、モデルはリングの数が平均以上である確率を0.3958と予測しました（つまり、P = 0.3958）。これにより、予測される対数オッズはf(x) = ln(0.3958/(1–0.3958)) = -0.423となります。

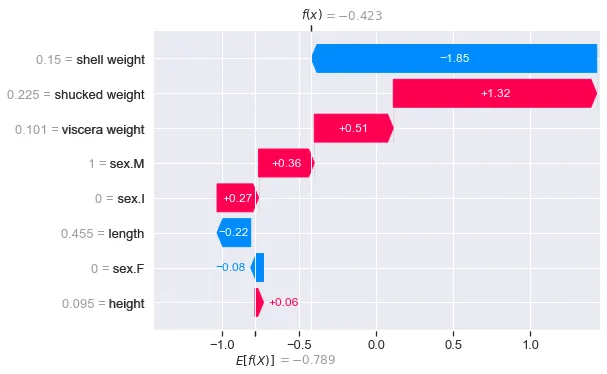
したがって、SHAP値は予測対数オッズと平均予測対数オッズの差を示します。正のSHAP値は対数オッズを増加させます。たとえば、shucked weightは対数オッズを1.32増加させました。つまり、この特徴はモデルが平均以上のリング数を予測する確率を増加させました。同様に、負の値は対数オッズを減少させます。

これらの値を以前と同じように集約することもできます。良いニュースは、ビースワームや平均SHAPなどのプロットの解釈は同じであることです。ただし、対数オッズを扱っていることを覚えておいてください。次に、多クラスの目標変数に対するこの解釈がどのように変わるかを見てみましょう。

多クラスの目標変数

3つのカテゴリ（young（0）、VoAGI（1）、old（2））を持つ新しい目標変数（y_cat）を作成します。前述の通り、この目標変数を予測するためにXGBoost分類器を訓練します（行5-6）。

# カテゴリカルな目標変数を作成
y_cat = [2 if y_>12 else 1 if y_>8 else 0 for y_ in y]
# モデルを訓練
model_cat = xgb.XGBClassifier(objective="binary:logistic")
model_cat.fit(X, y_cat)

このモデルでは、もはや「陽性の予測」とは言えません。これは、最初のインスタンスに対する予測確率を出力することで確認できます（行2）。これにより、[0.2562、0.1571、0.5866]が得られます。この場合、3番目の確率が最も高く、アワビはold（2）と予測されます。SHAPにとっては、陽性クラスの値だけを考慮することはできなくなります。

# 確率予測を取得
model_cat.predict_proba(X)[0]

SHAP値を計算すると（行2-3）、これが確認できます。コードは2値モデルと同じです。ただし、形状を出力すると（行5）、(4177, 8, 3)が得られます。これにより、各インスタンス、特徴量、クラスごとに1つのSHAP値が得られるようになりました。

# SHAP値を取得
explainer = shap.Explainer(model_cat)
shap_values_cat = explainer(X)
print(np.shape(shap_values_cat))

その結果、各クラスのSHAP値を個別のウォーターフォールプロットで表示する必要があります。以下のコードでは、最初のインスタンスに対してこれを行います。

# クラス0のウォーターフォールプロット
shap.plots.waterfall(shap_values_cat[0,:,0])
# クラス1のウォーターフォールプロット
shap.plots.waterfall(shap_values_cat[0,:,1])
# クラス2のウォーターフォールプロット
shap.plots.waterfall(shap_values_cat[0,:,2])

図3はクラス0のウォーターフォールプロットを示しています。値は各特徴量がこのクラスのモデル予測にどのように寄与したかを示しています。これは、このクラスに対する平均予測と比較しています。確率が比較的低い（つまり0.2562）ことがわかります。この低い確率に対して、shucked weight特徴量が最も重要な貢献をしました。

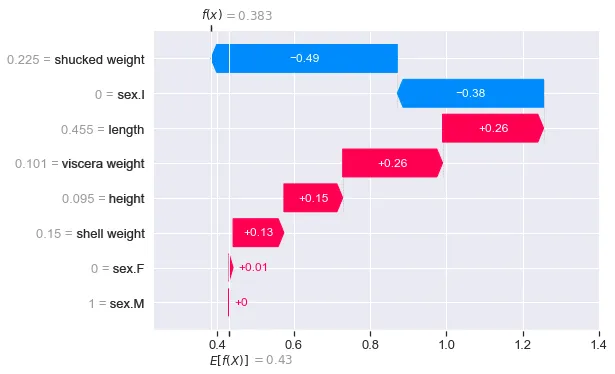
図4は他のクラスの出力を示しています。クラス2に対してf(x) = 1.211が最大であることに気付くでしょう。これは、このクラスの確率も最大であったためです（0.5866）。このインスタンスのSHAP値を分析する際には、このウォーターフォールプロットに焦点を当てることが意味があるかもしれません。これはこのアバロンのクラスの予測です。

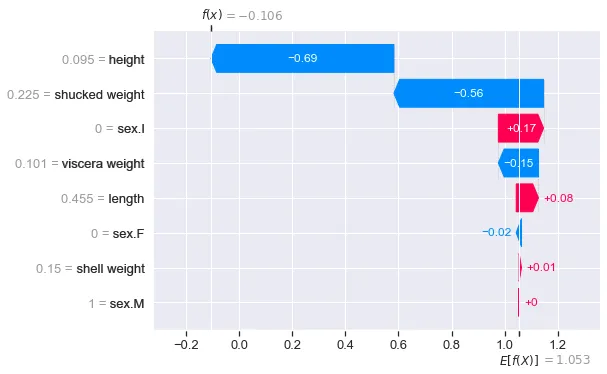
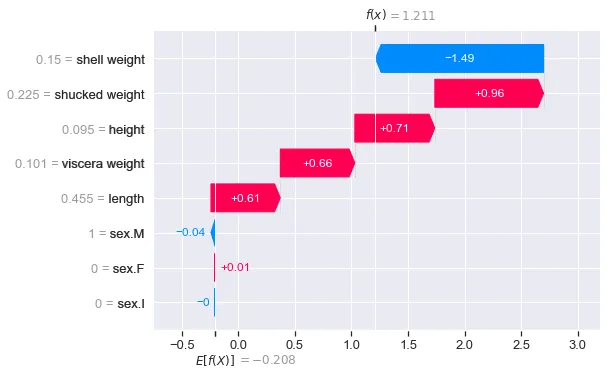
Softmaxによる値の解釈

複数のクラスに対して取り扱っているため、f(x)はsoftmaxで与えられます。以下の関数を使用して、softmax値を確率に変換することができます。 fxは上記のウォーターフォールプロットの3つのf(x)の値を表しています。結果は[0.2562, 0.1571, 0.5866]です。先ほどのインスタンス0の予測確率と同じです！

def softmax(x):    """各スコアのsoftmax値を計算する"""    e_x = np.exp(x - np.max(x))    return e_x / e_x.sum(axis=0)# softmaxを確率に変換するfx = [0.383,-0.106,1.211]softmax(fx)

多クラスのSHAP値の集約

これらのSHAP値は、SHAPプロットのいずれかを使用して集約することができます。ただし、ウォーターフォールと同様に、クラスごとに個別のプロットが存在します。これらを分析することは手間がかかります。特に対象変数に多くのカテゴリがある場合はそうです。そのため、集計の他のアプローチについても説明します。

最初のものは平均SHAPプロットのバージョンです。各クラスごとのSHAP値の絶対平均を計算します（2-4行目）。次に、各クラスと特徴量ごとに棒グラフを作成します。

# 各クラスごとの平均SHAP値を計算mean_0 = np.mean(np.abs(shap_values_cat.values[:,:,0]),axis=0)mean_1 = np.mean(np.abs(shap_values_cat.values[:,:,1]),axis=0)mean_2 = np.mean(np.abs(shap_values_cat.values[:,:,2]),axis=0)df = pd.DataFrame({'small':mean_0,'VoAGI':mean_1,'large':mean_2})# 平均SHAP値をプロットfig,ax = plt.subplots(1,1,figsize=(20,10))df.plot.bar(ax=ax)ax.set_ylabel('平均SHAP',size = 30)ax.set_xticklabels(X.columns,rotation=45,size=20)ax.legend(fontsize=30)

結果は図5に表示されます。1つ注意すべき点は、各棒がすべての予測に対する平均を示していることです。ただし、実際の予測クラスは各ケースで異なる場合があります。そのため、予測されたクラスを説明しないSHAP値により平均が歪む可能性があります。これがVoAGIクラスの平均が小さくなっている理由かもしれません。

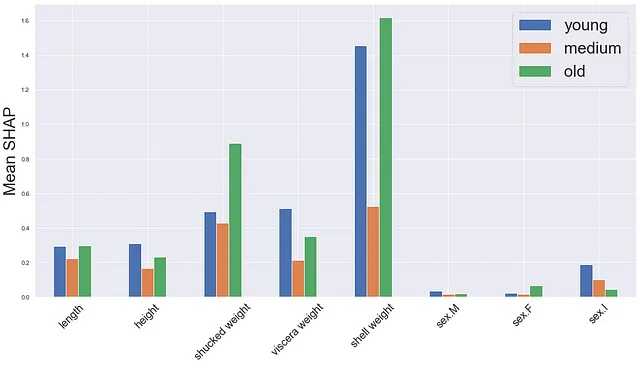
これを回避するために、予測されたクラスのSHAP値に焦点を当てることができます。各インスタンスの予測クラスを取得します（2行目）。新しいセットのshap値（new_shap_values）を作成します。これは元の値をループ処理し、そのインスタンスの予測に対応するセットのみを選択することで行われます（5-7行目）。

# モデルの予測結果を取得preds = model_cat.predict(X)new_shap_values = []for i, pred in enumerate(preds):    # 予測クラスのshap値を取得    new_shap_values.append(shap_values_cat.values[i][:,pred])

次に、元のオブジェクトのSHAP値を置き換えます（2行目）。これにより、形状が（4177, 8）になります。つまり、インスタンスごとに1つのSHAP値のセットに戻ります。

# shap値を置換shap_values_cat.values = np.array(new_shap_values)print(shap_values_cat.shape)

このアプローチの利点は、組み込みのSHAPプロットを簡単に使用できることです。たとえば、図6の平均SHAPプロットです。これらの値は、特徴量が予測クラスへの平均的な貢献を示していると解釈できます。

shap.plots.bar(shap_values_cat)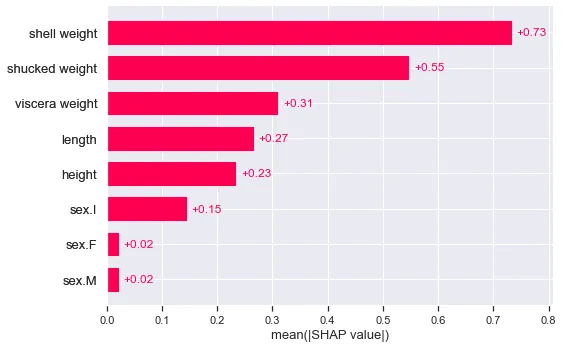

また、ビースワームも使用できます。ただし、SHAP値と特徴量の値の間に明確な関係が見られないことに注意してください。これは、特徴量は予測クラスによって異なる関係を持つためです。年齢が大きいアワビは大きくなります。したがって、たとえば大きな貝の重さは、古い（2）の予測の確率を高めます。若い（0）の予測では逆の関係があります。

shap.plots.beeswarm(shap_values_cat)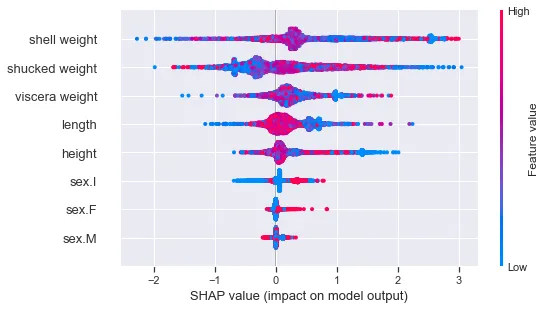

したがって、バイナリおよびマルチクラスターゲット変数のSHAP値の解釈方法が明確になったことを願っています。ただし、それらが対数オッズとソフトマックスで表されている理由について疑問に思うかもしれません。これは、SHAP値が計算される方法に起因します。つまり、線形モデルによって同時に行われることです。バイナリまたはマルチクラスターゲット変数を線形モデルで予測する場合、それぞれロジスティック回帰またはソフトマックス回帰を使用します。これらのリンク関数は微分可能であり、モデルの予測をパラメータと特徴量の線形方程式として定式化することを可能にします。同様に、これらの特性はSHAP値を効率的に推定するために使用されます。

shapについて詳しく学ぶ：

新しいSHAPプロット：バイオリンとヒートマップ

SHAPバージョン0.42.1のプロットがモデルについて教えてくれること

towardsdatascience.com

SHAPの制約事項

特徴量の依存関係、因果推論、および人間のバイアスがSHAPに影響を与える方法

towardsdatascience.com

SHAPを使用してPyTorchイメージ回帰モデルをデバッグする

自動運転車を駆動するモデルを理解し、改善するためにDeepShapを使用する

towardsdatascience.com

この記事がお楽しみいただけたと思います！私の紹介されたメンバーの1人になることで、私をサポートしていただけます🙂

私の紹介リンクでVoAGIに参加する — コナー・オサリバン

VoAGIのメンバーとして、あなたの会費の一部があなたが読んだ作家に送られ、すべてのストーリーに完全アクセスできます…

conorosullyds.medium.com

| Twitter | YouTube | ニュースレター — Python SHAPコースへの無料アクセスをご登録ください

参考文献

Stackoverflow SHAPを使用したマルチクラス分類問題のbase_valueの解釈方法は？https://stackoverflow.com/questions/65029216/how-to-interpret-base-value-of-multi-class-classification-problem-when-using-sha/65034362#65034362

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!