データサイエンスにおける統計学：理論と概要

データサイエンスにおける統計学の理論と概要

 

データサイエンスのインタビューで目立つために統計学をマスターすることに興味はありますか？ インタビューのためだけにそれを行うべきではありません。統計学を理解することで、データからより深く詳細な洞察を得ることができます。

本記事では、データサイエンスの問題解決能力を向上させるために知っておく必要のある最も重要な統計の概念を紹介します。

 

• テキストから音声へ – 大規模な言語モデルのトレーニング
• LLMとデータ分析：ビジネスの洞察を得るためにAIがビッグデータを理解する方法
• 「PhysObjectsに会いましょう：一般的な家庭用品の36.9K個のクラウドソーシングと417K個の自動物理的概念アノテーションを含むオブジェクト中心のデータセット」

統計学の概要

 

統計学について考えると、最初に思い浮かぶのは何ですか？ 頻度、割合、平均など、数値で表される情報を思い浮かべるかもしれません。テレビのニュースや新聞を見ると、世界のインフレデータ、自国の雇用者数と失業者数、通りでの死亡事故のデータ、アンケート調査による各政党の投票割合など、これらの例はすべて統計です。

これらの統計情報の作成は、統計学と呼ばれる学問の最も明白な応用です。統計学は、経験的なデータの収集、解釈、提示のための方法を開発し、研究する科学です。さらに、統計学の領域は、記述統計学と推測統計学の2つの異なる分野に分けることができます。

年次国勢調査、度数分布、グラフ、数値要約は、記述統計学の一部です。 推測統計学では、サンプルと呼ばれる人口の一部に基づいて結果を一般化するための方法のセットを指します。

データサイエンスのプロジェクトでは、ほとんどの時間がサンプルとの取り扱いに費やされます。したがって、機械学習モデルで得られる結果は近似値です。モデルはその特定のサンプルでうまく機能するかもしれませんが、新しいサンプルでは性能が良くなるわけではありません。すべては私たちのトレーニングサンプルに依存し、その特徴をよく一般化するためには代表的なものでなければなりません。

 

グラフと数値要約によるEDA

 

データサイエンスのプロジェクトでは、探索的データ分析（EDA）は最も重要なステップであり、要約統計量とグラフィカルな表現を用いてデータの初期調査を行うことができます。また、パターンの発見、異常値の発見、仮定のチェックにも役立ちます。さらに、データに含まれるエラーを見つけるのにも役立ちます。

EDAでは、主な焦点は変数にあります。変数は2つのタイプに分類されます：

• 数値変数は数値の尺度で測定される変数です。離散的または連続的に分類することができます。離散変数は区別可能な数量です。離散変数の例としては、学位の評価と家族の人数があります。連続変数は、可能な値の集合が有限または無限の区間内にある変数です。例としては身長、体重、年齢があります。
• カテゴリ変数は通常2つ以上のカテゴリで構成される変数です。例えば、職業の状態（雇用中、失業中、求職中）や仕事の種類です。数値変数と同様に、カテゴリ変数は順序尺度と名義尺度の2つの異なるタイプに分けることができます。変数がカテゴリの順序を持つ場合、順序尺度です。例としては、低い、VoAGI、高いレベルの給与があります。カテゴリ変数が順序を持たない場合、名義尺度です。名義変数の例としては、女性と男性の性別があります。

 

一変量データのEDA

 

 

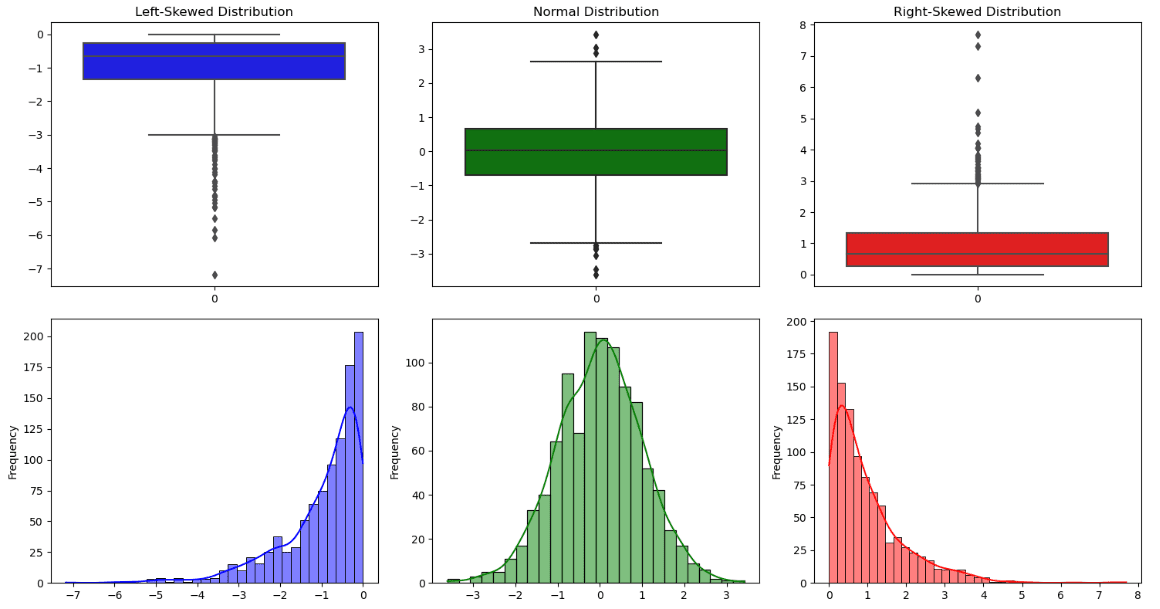
数値変数を理解するためには、通常、各変数の統計情報の概要を得るためにdf.describe()を使用します。出力には、カウント、平均値、標準偏差、最小値、最大値、中央値、第1四分位数、第3四分位数が含まれています。

これらの情報は、ボックスプロットと呼ばれるグラフィカルな表現でも見ることができます。ボックスの横線は中央値を表し、下部ヒンジと上部ヒンジはそれぞれ第1四分位数と第3四分位数に対応します。ボックスが提供する情報に加えて、分布の両側を表す2本の線、ヒゲとも呼ばれる線があります。ヒゲの境界外のすべてのデータポイントは外れ値です。

このプロットから、分布が対称的か非対称的かを観察することも可能です：

• 分布は対称的であるとき、ベル型の形状であり、中央値は平均値とほぼ一致し、ウィスカーの長さも同じです。
• 分布は右に偏った（正偏差）場合、中央値は第三四分位数に近いです。
• 分布は左に偏った（負偏差）場合、中央値は第一四分位数に近いです。

分布の他の重要な側面は、各区間にいくつのデータポイントが含まれるかを数えるヒストグラムから可視化することができます。以下の4つの形状が観察できます：

• 1つのピーク/モード
• 2つのピーク/モード
• 3つ以上のピーク/モード
• 明確なモードがない均一分布

変数がカテゴリカルな場合、最良の方法は、特徴の各要素の頻度表を観察することです。より直感的な可視化のために、変数に応じて垂直または水平バーを使用した棒グラフを使用することができます。

 

二変量データのEDA

 

 

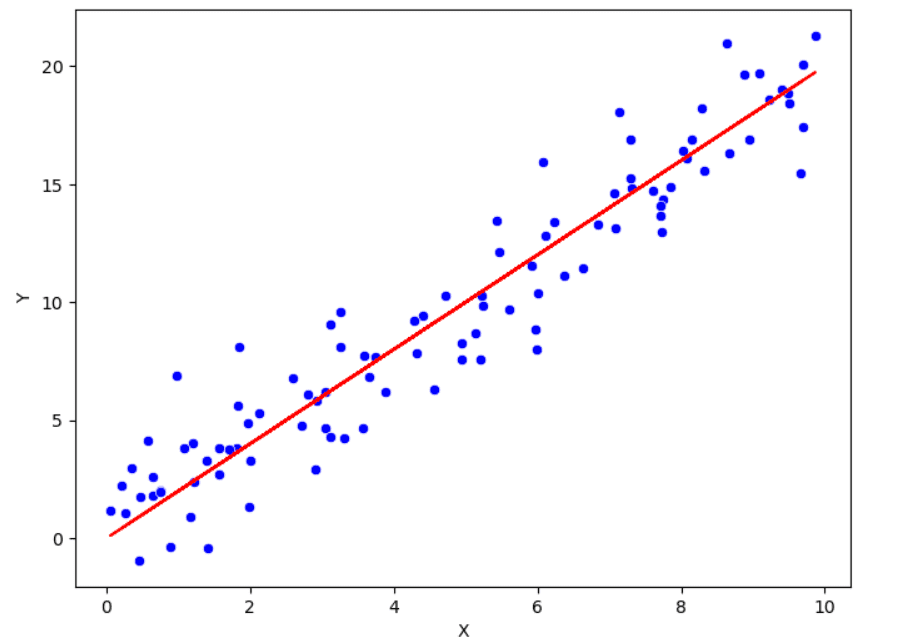
以前に一変量分布を理解するためのアプローチをリストアップしました。今度は、変数間の関係を研究する時です。この目的のために、2つの変数間の線形関係を測るピアソン相関係数を計算することが一般的です。この相関係数の範囲は-1から1の間です。相関の値がこれら2つの極端に近いほど、関係は強くなります。0に近い場合、2つの変数間には弱い関係があります。

相関に加えて、2つの変数間の関係を可視化するための散布図もあります。このグラフィカルな表現では、各点は特定の観測値に対応します。データ内の変動が多い場合にはあまり情報を提供しません。変数のペアからより多くの情報を把握するために、平滑化された線を追加したり、データを変換したりすることがあります。

 

確率分布

 

確率分布の知識はデータを扱う際に重要です。

データサイエンスで最も使用される確率分布は以下の通りです：

• 正規分布
• カイ二乗分布
• 一様分布
• ポアソン分布
• 指数分布

 

正規分布

 

 

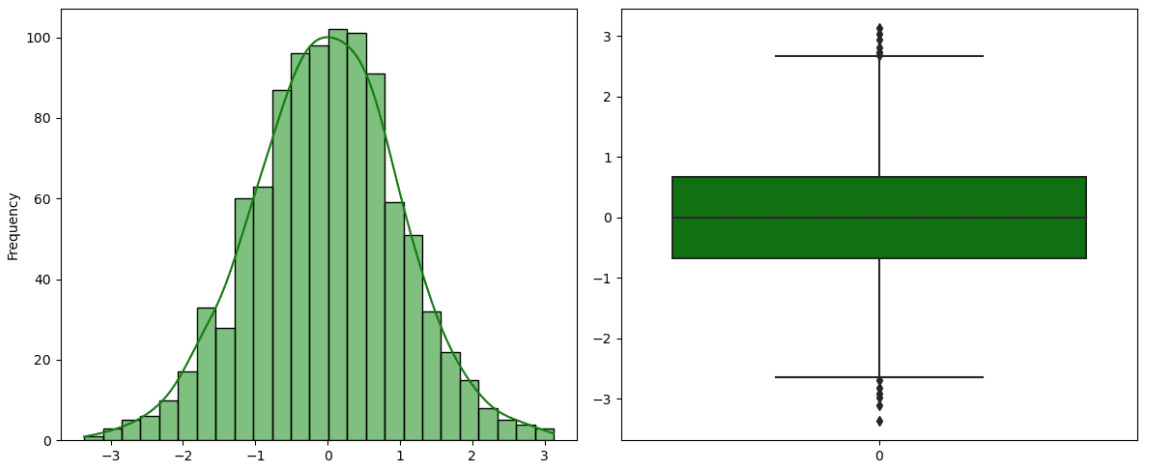
正規分布は、統計学で最も一般的な分布であり、ガウス分布とも呼ばれています。特徴的な形状のため、ベルカーブとして知られており、中央部分が高く、両端に向かって裾野が広がっています。対称的で単峰性であり、ピークを持ちます。また、正規分布には平均値と標準偏差という2つの重要なパラメータがあります。平均値はピークと一致し、曲線の幅は標準偏差で表されます。特に、平均値が0で分散が1である特殊なタイプの正規分布である標準正規分布があります。これは元の値から平均値を引き、標準偏差で割ることで得られます。

 

スチューデントのt分布

 

 

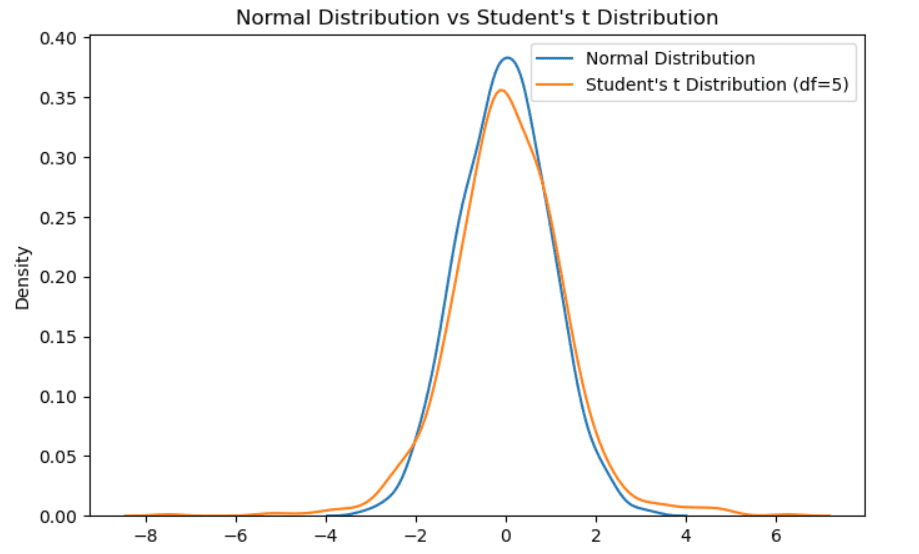
自由度vのt分布とも呼ばれます。標準正規分布と同様、ゼロを中心に対称的で単峰性です。ただし、ガウス分布とは異なり、中央部分の質量が少なく、裾野により多くの質量があります。サンプルサイズが小さい場合に考慮されます。サンプルサイズが増えるほど、t分布は正規分布に収束していきます。

 

カイ二乗分布

 

 

これはガンマ分布の特殊なケースであり、仮説検定や信頼区間での応用でよく知られています。もし、正規分布に従う独立したランダム変数の集合がある場合、それぞれのランダム変数の値を二乗してその値を合計すると、最終的なランダムな値はカイ二乗分布に従います。

 

一様分布

 

 

これはデータサイエンスのプロジェクトでよく見かける人気のある分布です。すべての結果が等しい確率で発生するという考え方です。代表的な例として、６面ダイスを振ることが挙げられます。ダイスの各面が等しい確率で出るため、結果は一様分布に従います。

 

ポアソン分布

 

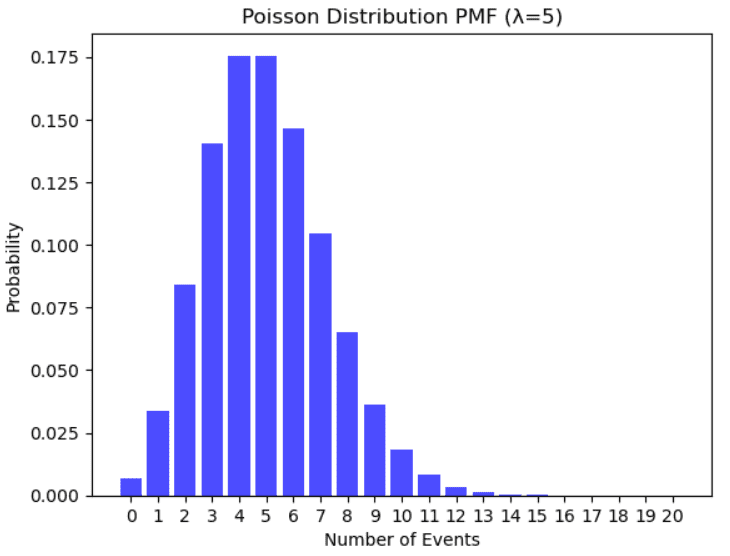ポアソン分布の例。著者によるイラスト。  

これは特定の時間間隔内でランダムに多くの回数発生するイベントの数をモデル化するために使用されます。ポアソン分布に従う例として、100歳以上の人口、システムの1日あたりの障害の数、特定の時間枠でヘルプラインに到着する電話の数などがあります。

 

指数分布

 

指数分布の例。著者によるイラスト。  

これは特定の時間間隔内でランダムに多くの回数発生するイベント間の時間の量をモデル化するために使用されます。例としては、ヘルプラインでの待ち時間、次の地震までの時間、がん患者の残りの生存年数などがあります。

 

仮説検定

 

仮説検定は、サンプルデータに基づいて母集団についての仮説を立て、評価する統計的手法です。つまり、推測統計の一形態です。このプロセスは、検定する必要がある母集団のパラメータに関する仮説、つまり帰無仮説と呼ばれるものから始まります。対立仮説（H1）はその逆の主張を表します。データが仮定と非常に異なる場合、帰無仮説（H0）は棄却され、結果は「統計的に有意」と言われます。     

仮説が指定された後、以下のステップがあります：

• 有意水準を設定します。これは帰無仮説を棄却するために使用される基準です。一般的な値は0.05と0.01です。このパラメータは、帰無仮説が棄却されるまでの実証的な証拠の強さを決定します。  
• 統計量を計算します。これはサンプルから計算される数値です。これは、エラーリスクをできるだけ限定するための意思決定のルールを決定するのに役立ちます。 
• p値を計算します。これは、帰無仮説で指定されたパラメータと異なる統計量を得る確率です。p値が有意水準（例：0.05）以下である場合、帰無仮説を棄却します。p値が有意水準よりも大きい場合、帰無仮説を棄却することはできません。

様々な種類の仮説検定が存在します。データサイエンスのプロジェクトで線形回帰モデルを使用したいとしましょう。線形回帰モデルは正規性、独立性、線形性の強い仮定を持つことで知られています。統計モデルを適用する前に、糖尿病患者の成人女性の体重に関する特徴の正規性をチェックしたいとします。その場合、シャピロ・ウィルク検定が役立ちます。また、PythonのScipyというライブラリには、この検定の実装が含まれています。この検定では、変数が正規分布に従うという帰無仮説があります。p値が有意水準（例：0.05）以下の場合、帰無仮説を棄却します。p値が有意水準よりも大きい場合、変数は正規分布に従うという帰無仮説を受け入れることができます。  

 

最後の考え

 

このイントロダクションが役に立ったと思います。統計を修得することは、理論に続いて実践的な例を学ぶことで可能だと考えています。ここでカバーしていない重要な統計概念もきっとありますが、私はデータサイエンティストとしての経験で役立つと考えた概念に焦点を当てることを選びました。あなたの仕事で役に立った他の統計的手法は知っていますか？洞察に富んだ提案があれば、コメントで教えてください。

参考資料:

• HyperStat オンライン統計テキストブック
• 位置の指標
• データサイエンスで最も使用される確率分布

    Eugenia Anello は現在、イタリアのパドヴァ大学情報工学部の研究員です。彼女の研究プロジェクトは持続的学習と異常検知の組み合わせに焦点を当てています。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!