ソートアルゴリズムの概要：ヒープソート

ソートアルゴリズムの概要：ヒープソート

ヒープデータ構造とソートに使用される方法を学ぶ

はじめに

ヒープは、配列をバイナリツリーベースの形式で表すデータ構造です。ヒープは以下のルールを持ちます：

• 完全性。ヒープの各レベルは要素で完全に埋められています。ただし、最後のレベルは左側から部分的に要素が埋まっている場合があります。
• ヒープルール。親ノードの値は、子ノードの値以下である必要があります。この条件が満たされる場合、ヒープはミンヒープと呼ばれます。親の値が子の値よりも大きい場合、マックスヒープというバリエーションも存在します。

この記事では、ミンヒープの例とコードを提供します。マックスヒープのアルゴリズムのワークフローは非常に似ています。以下にミンヒープの例を示します。

• ソートアルゴリズムの概要：クイックソート
• 「AIイノベーションのためのニューロエボリューションの活用」
• 「Falcon 180B あなたのコンピューターで動作しますか？」

ヒープは通常、配列の形で格納されます。親ノードのインデックスがiの場合、その左の子の位置は2 * i + 1、右の子の位置は2 * i + 2です。逆に、非ルートノードのインデックスがiの場合、親ノードのインデックスは(i – 1) // 2です。この原則に従って、上記のヒープの配列表現を得ることができます：

操作

ヒープは、以下の操作をサポートしています：

• ノードの挿入
• 配列からのヒープの構築
• 最小値を持つノードの抽出
• ソート

ヒープデータ構造は複数の操作を持つため、クラスとして実装する方が実用的です。今のところ、基本的な実装を行います。各操作の後に、対応するコードスニペットが提供されます。

• heapフィールドは、ヒープの形式で入力配列を格納します（後で実装されます）
• _swap()メソッドは、配列の2つのインデックスを取り、それらの値を交換します。
• _number_of_children()メソッドは、ノードが持つ子の数（0、1、または2）を返します。

ノードの挿入

ヒープへの新しい要素は最後の位置に挿入されます。この挿入は、新しい要素が親の値よりも小さい場合にヒープルールを破壊する可能性があります。この問題を避けるために、新しいノードは再帰的に上に伝播し、ヒープルールを破らないようになるまで続けられます。この手順はヒープ化（上向き）と呼ばれます。

上記の図から、値が3のノードを挿入します。

• 挿入後、ヒープルールが破られます。3 < 15（親）なので、要素3と15を交換します。
• ノード3には値が7の新しい親があります。再び、ヒープルールが満たされないため、3と7を交換します。
• ノード3はインデックス2にあり、値が1の親を持っています。3 ≥ 1なので、ヒープルールは正しいです。この段階で挿入手順は終了です。

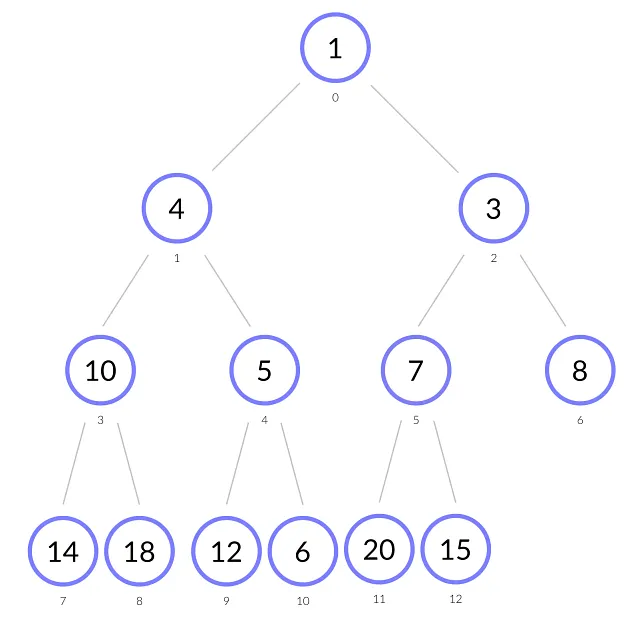
挿入の時間計算量を調べましょう。最悪の場合は、新しいノードを木の下から上のレベルまで伝播する必要がある場合です。任意の木の高さは要素の総数Nに対して対数的であり、各比較にはO(1)の時間がかかるため、最終的な推定結果はO(logN)の時間となります。

• insert() メソッドは値をヒープに追加し、その後、ヒープ化するメソッドを呼び出します。
• _heapify_up() メソッドは、ヒープのルールが正しくなるまで親ノードに再帰的に自身を呼び出します。

ヒープの構築

入力配列の各要素に対して、挿入手順が呼び出されます。これがヒープの構築方法です。

計算量については、各要素に対して O(logN) の時間で動作する関数を呼び出すため、ヒープの構築には O(N * logN) の時間がかかるように思えるかもしれません。しかし、その推定を改善し、合計時間が O(N) であることを数学的に証明することができます。

• build() メソッドの渡された配列に対して、挿入呼び出しを行いヒープを構築します。

最小値のノードの抽出

最小値のノードはヒープの一番上にあります。最小値を抽出し、ヒープの一番上のノードを最後のノードで置き換えます。ヒープのルールが破られるので、この要素を下に伝播します。アルゴリズムは前述の挿入時に使用したものと非常に似ています（要素が上に伝播されました）：各ステップで、現在の要素を最小値を持つ子と交換します。この手続きは、ヒープのルールが破られなくなるか、現在の要素に子がなくなるまで続きます。

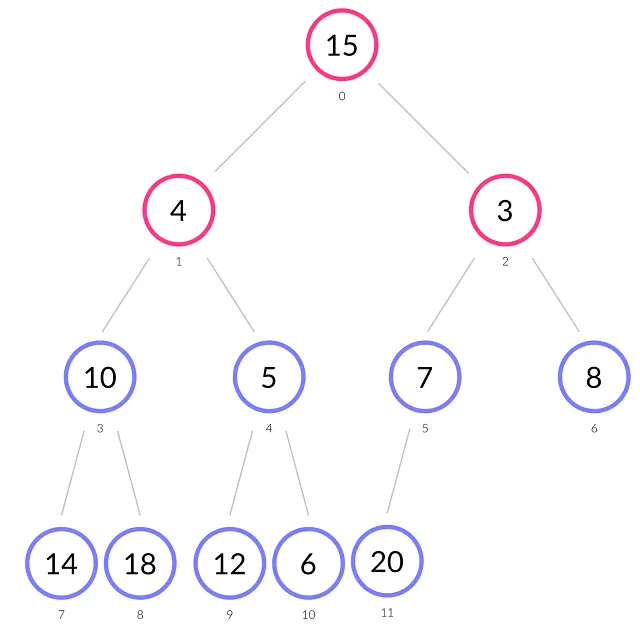
上の図では、値が1のノードが抽出され、値が15の最後のノードがその位置を占めています。

• ノード15がヒープのルールを破っているため、最小の子である3と交換します。
• その後、ノード15には7と8という劣った子があります。再び、最小の子である7と交換します。
• その後、15はインデックス5にあり、唯一の子である20があります。15 ≤ 20 なので、ヒーピファイ手続きを終了します。

挿入セクションのヒーピファイアルゴリズムと同様に、このアルゴリズムも同じ漸近表現を持ち、O(logN) の時間で実行されます。

ソート

ソートは最小値のノードの抽出を介して実装されます。ヒープが空でない間、extract_min() 関数を呼び出し、最小の要素を新しい配列に追加します。これにより、配列はソートされた要素で構成されます。

ヒープにはN個のノードが含まれ、extract_min() はO(logN) の時間で動作するため、ソートの合計時間は O(N * logN) かかります。

結論

ヒープの全ての主要な操作をカバーしました。ヒープデータ構造を使用して配列をソートするには、まずヒープを構築し、それからそれに対してソートメソッドを呼び出す必要があります。ヒープの構築にはO(N) の時間がかかり、ソートにはO(N * logN) の時間がかかり、最終的にはヒープソートの漸近表現が O(N * logN) になります。

Heap クラスの完全な実装は以下に示されています。

特記されていない限り、すべての画像は著者によるものです。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!