ソートアルゴリズムの概要:クイックソート
ソートアルゴリズムの概要:クイックソート
最も効率的なソーティングアルゴリズムを発見する

はじめに
クイックソートはおそらく最も人気のあるソーティングアルゴリズムです。多くの実験では、平均的に他のソーティング方法(マージソートやヒープソートなど)よりも優れたパフォーマンスを示していることが示されています。
クイックソートは、配列を再帰的に二つの部分に分割するというアイデアに基づいています。一つはピボット要素よりも小さい要素を含む部分で、もう一つは大きい要素からなる部分です。この手続きはパーティションと呼ばれます。パーティション関数は、配列の分割された部分に対して再帰的に呼び出され、パーティションする要素が1つだけになるまで続けられます。
パーティション
最初に、ピボット要素を選ぶ必要があります。これは配列の任意の要素にすることができます。この例では、最後の配列要素を選びます。次に、現在の要素をピボットと比較するループを実行します。要素がピボット以下であれば、左側の配列に保持されます。それ以外の場合、要素は右側に移動されます。
まず、iとjの2つのポインタを初期化します。jは最初の要素を指し、iはその1つ前の値j-1を指します。導入された変数iとjによって、以下の不変条件がループ全体で満たされます:
- インデックス[left, i]の要素はピボット以下である。
- インデックス[i + 1, j)の要素はピボットよりも大きい。
ループの終了時に、jはrightと等しくなり、インデックスiは配列を二つの部分に分けます。真の不変条件のおかげで、配列は正しくパーティションされます。
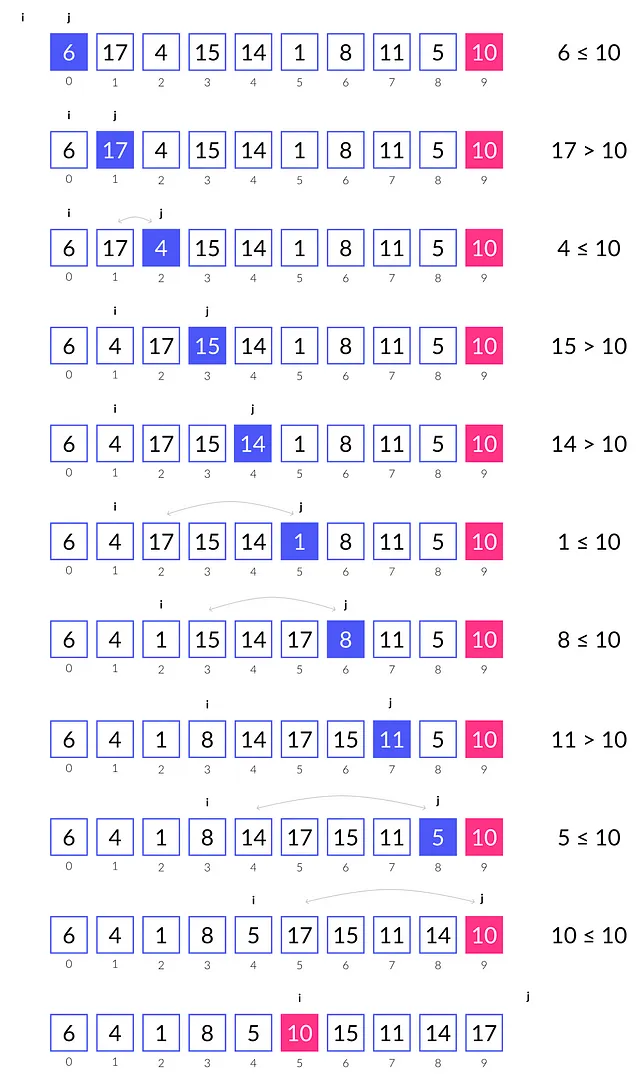
各イテレーションで、jは1増加するため、常に現在の要素を指します。次に、現在の要素array[j]はピボットと比較されます。要素がピボット以下であれば、位置i + 1の要素と交換されます。上記の不変条件によれば、常にarray[i + 1] > ピボットであることがわかります。その結果、ピボット以下の要素は、ピボットよりも大きい要素と左方向に交換されます。このような交換を行うことで、不変条件が破られます。これに対応して、iは1増加します。
array[j] > ピボットの場合、不変条件は依然として正しいため、単純に次のイテレーションに進みます(iの値は変化しません)。
すべてのイテレーションの後、配列は正しくパーティションされます。上記のロジックは以下のコードスニペットで示されています。注目すべきは、ピボット要素のインデックスが返されることです。
パーティション関数
ソート
ソーティングアルゴリズムは再帰的に進行します。まず、前のセクションに基づいて、配列は二つの部分に分割されます。それぞれに対して、パーティション手続きが再帰的に呼び出され、パーティションする要素が1つだけになるまで続けられます。
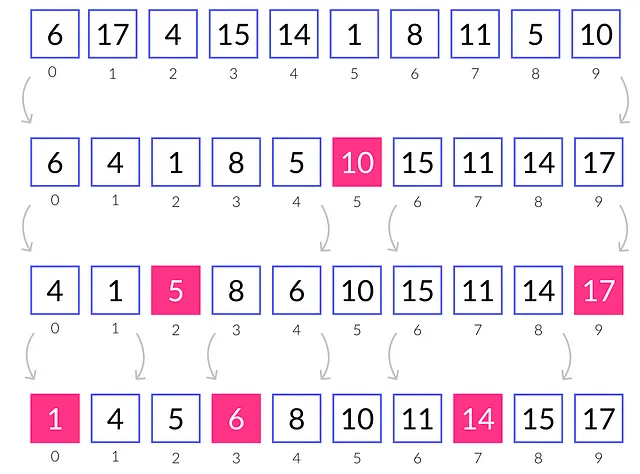
このアルゴリズムの関数は以下のとおりです。
クイックソート関数
計算量
クイックソートの正確な漸近的証明は詳細が多く、比較的複雑なため、すべての側面について深く掘り下げることは避けたいと思います。代わりに、非形式的な証明を提供します。
各パーティション呼び出しの間、配列のすべての要素を線形に通過するため、O(K)の計算量が発生します(ここでKは配列のサイズです)。各パーティション手続きの後、ピボット要素が配列を二等分すると仮定し、両方の部分に対して再帰的にクイックソート関数を呼び出すと、ソートされる要素が1つだけになるまで同じ関数呼び出し構造が生成されます。この構造はマージソートと同じです。

唯一の違いは、マージ関数の代わりにパーティション関数を呼び出すことですが、両者の時間計算量はO(K)と同じです。階層構造も同じであるため、クイックソートの時間計算量はO(N * logN)となります。マージソートの漸近的な証明はこちらで見つけることができます。
ソートアルゴリズム、パート1:マージソート
ソートに関する話題では、マージソートは最も人気のあるアルゴリズムの1つです。これは有名な…
VoAGI.com
上記の証明では、常に配列が2つの等しい半分に分割されると仮定していますが、これは明らかに常に真ではありません。パーティション手順が常に他の要素と1つの要素のみを分離すると仮定しましょう。これにより、パーティション手順が呼び出されるすべての反復において、配列のサイズはN – 1、N – 2、N – 3、…、1になります。算術進行の総和の公式を使用して、このシナリオの合計時間計算量を計算しましょう。
T(N) = O(N) + O(N – 1) + O(N – 2) + O(N – 3) + … + O(1) = O(N * (N + 1) / 2) = O(N²)
結果として、二乗の時間計算量になります。これはクイックソートの最悪のケースです。ただし、このシナリオの発生確率は非常に小さいです。
平均的には、クイックソートはO(N * logN)の時間で動作し、他のソートアルゴリズムよりも優れた性能を発揮します。
クイックソートを内部で使用するシステムを開発すると想像してください。配列の最後の要素を常に選ぶという同じ原則に従うことは良いアイデアではありません。誰かがシステムでピボット要素の選択戦略を見つけ出すと、その人は最悪のパーティションシナリオを引き起こす配列を明示的に入力することができ、その結果としてO(N²)の時間計算量になります。これはシステムの効率を大幅に低下させる可能性があります。そのため、各反復ごとに異なる方法でピボットを選択することが常に良いです。最も一般的な方法の1つは、ランダムにピボットを選択することです。
結論
クイックソート、ソートのためのよく知られたアルゴリズムを学びました。最悪のシナリオでは二次の計算量を持っていますが、実際の場面では他のアルゴリズム(マージソートやヒープソートなど)と比較して、特に大きな配列の場合には通常よりも優れたパフォーマンスを発揮します。
特記しない限り、すべての画像は著者によるものです
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles

