クラスの不均衡:SMOTEからSMOTE-NCおよびSMOTE-Nへ
クラスの不均衡:SMOTEからSMOTE-NCおよびSMOTE-Nへ' Condensed 'クラスの不均衡:SMOTE-NCおよびSMOTE-Nへ
クラスの不均衡問題に対処するための3つのアルゴリズムの探索
前のストーリーでは、単純なランダムオーバーサンプリングとランダムオーバーサンプリングの例(ROSE)アルゴリズムの動作方法を説明しました。さらに重要なことに、クラスの不均衡問題を定義し、それに対する解決策を直感的に導き出しました。クラスの不均衡について明確な理解を確保するために、そのストーリーを確認することを強くお勧めします。
このストーリーでは、SMOTE、SMOTE-NC、SMOTE-Nの3つのアルゴリズムについて考えます。ただし、それに先立ち、前のストーリーで考慮した2つのアルゴリズムが次の実装フレームワークに適合することを指摘することが重要です:
- クラスXに属するデータをアルゴリズムが取得し、Nxの例が必要な場合、オーバーサンプリングによってそのような例を計算する
- 一定の比率のハイパーパラメーターが与えられた場合、各クラスに追加する必要のあるポイントの数を計算する
- 各クラスに対してアルゴリズムを実行し、新たに追加されたすべてのポイントを元のデータと組み合わせて最終的なオーバーサンプリングデータセットを形成する
ランダムオーバーサンプリングとROSEアルゴリズムの両方についても、クラスXのNxの例を生成するためにアルゴリズムが次のように行われることも真実でした:
- クラスXに属するデータからランダムにNxのポイントを置き換えて選択する
- 選択された各ポイントに対してロジックを実行して新しいポイントを生成する(例:複製またはガウス分布を配置してサンプリングするなど)
このストーリーで考慮する他のアルゴリズムも同じフレームワークに適合することがわかります。
SMOTE(Synthetic Minority Oversampling Technique)
したがって、SMOTEが行うことを説明するために、1つの質問に答えるだけで十分です。クラスXからランダムに選択されたNxの例それぞれに対して、どのようなロジックが適用され、Nxの新しい例が生成されるのでしょうか?
答えは次のとおりです:
- ポイントのk個の最近傍を見つける(kはアルゴリズムのハイパーパラメーター)
- その中からランダムに1つを選択する
- ポイントからランダムに選択した最近傍への線分を引く
- その線分上のランダムなポイントを選択する
- 新しいポイントとして返す
数学的には、
- もし点x_iが最近傍の点z_i1、z_i2、…、z_ikを持っている場合
- jが[1,k]の範囲のランダムな数であり
- rが[0, 1]の範囲のランダムな数である場合
それぞれの点x_iに対して、SMOTEは次のように単純に適用することで新しい点x_i’を生成します:

これがSMOTEアルゴリズムが行うことです。点x_iから始めて、ベクトルz_ij – x_iの距離rを歩き、新しい点を配置します。

さらに補足すると、アルゴリズムの動作方法は、論文で説明されている方法とはわずかに異なることにも注意が必要です。特に、著者たちは比率が整数であると仮定しています(整数でない場合は切り捨てます)。クラスXの比率が整数Cの場合、それに属する各ポイントについて、ランダムに置換してC回の回数だけランダムな近傍を選択して、SMOTEのロジックを適用します。 実際には、SMOTEが実装されると、私たちが説明したように、浮動小数点数の比率で動作するように一般化されることが一般的です。つまり、Nxのポイントをランダムに選択してそれぞれにSMOTEを適用します。整数の比率(C=2など)の場合、各ポイントが平均して2回選択されるため、元のアルゴリズムに戻ります。これは、整数の比率でのオーバーサンプリングからランダムオーバーサンプリングに遷移することと、前のストーリーで説明されたものと同じです。
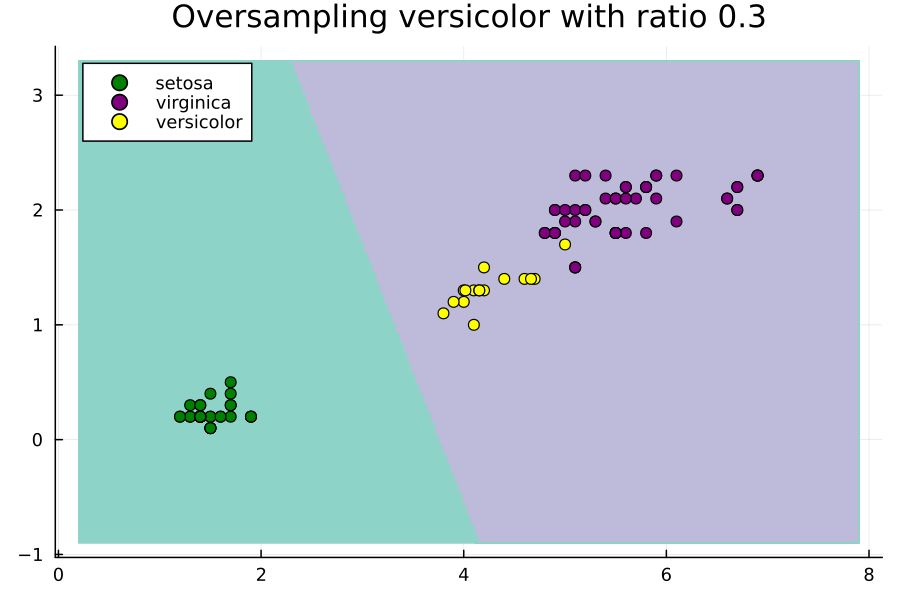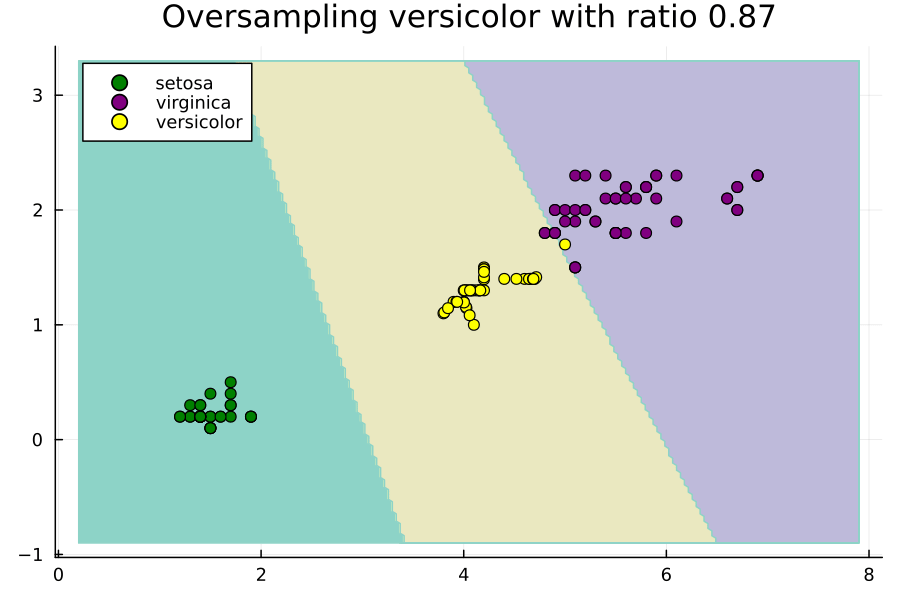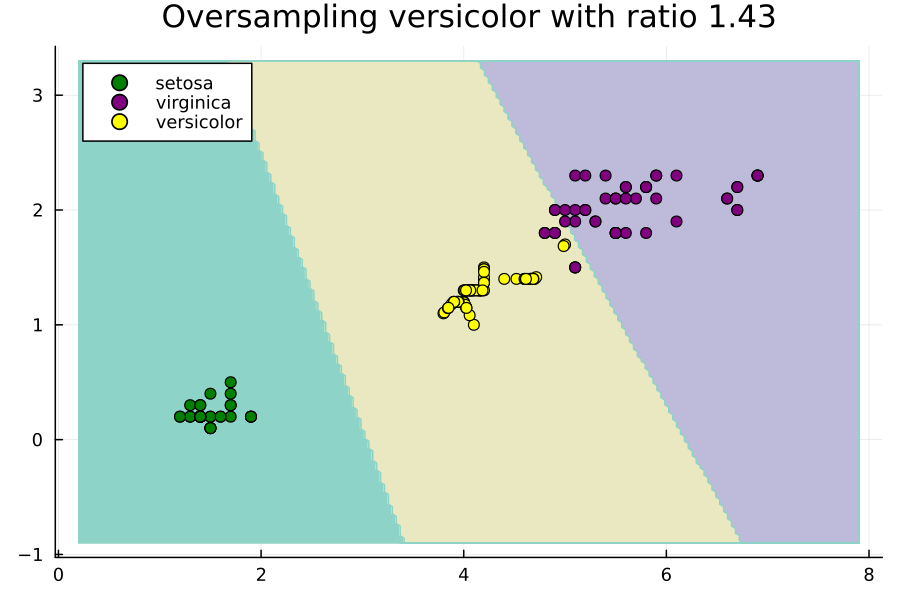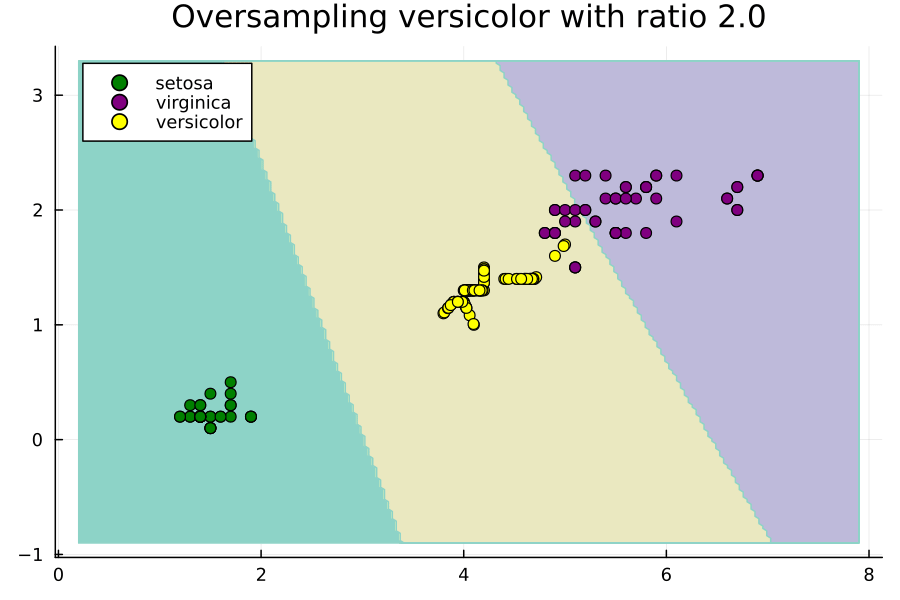
このアニメーションは、Irisデータセットの不均衡な部分集合に対してversicolorクラスのオーバーサンプリング比率を変更することで、SVMの決定領域がどのように変化するかを示しています。ここでの比率は、多数派クラスのサイズに対する相対的なものです。つまり、比率が1.0の場合、versicolorクラスがvirginicaクラスと同じ数の例を持つようにNxを設定します。
なぜSMOTEがROSEよりも優れているのか考えてみるかもしれません。結局のところ、SMOTEのポイント生成のロジックは論文で正当化されていません。一方、ROSEで行われるP(x | y)の推定からサンプリングすることは、はるかに合理的で直感的です。問題の1つは、P(x | y)の良い推定値を得るには多くのデータが必要である可能性があることですが、少数クラスには通常少ないデータがあることはわかっています。データが多くない場合、2つのオプションがあります:
- 過学習の可能性があるため、帯域幅を小さく選択する(random oversamplingと同様)
- それが極端な場合には、単に特徴空間からランダムにポイントを均等に追加することと同等です(つまり、非現実的な例)
考えてみると、SMOTEではこの問題を心配する必要はありません。データを完全に分離するハイパープレーンが存在する場合、SMOTEを適用してもその解決策は存在し続けます。実際、SMOTEがポイントを生成する方法によって、非線形の超曲面がより線形になる可能性があり、モデルが過学習を引き起こすリスクがはるかに低くなるようです。
SMOTE-NC(SMOTE-Nominal Continuous)
ROSEとSMOTEの両方は、単純なランダムオーバーサンプリングよりもはるかに改善された結果を提供するようですが、カテゴリ変数を扱う能力を失うという欠点もあります。SMOTEの著者は、カテゴリ特徴が存在する場合にも対処するために、SMOTEアルゴリズムの拡張を開発するという方法を考えつくほど賢いです。
カテゴリ特徴をエンコードすることでこれを回避できると思うかもしれませんが、SMOTEやROSEはそれらを連続として扱い、無効な値を生成します。たとえば、特徴がバイナリである場合、選択した点の値は新しい点のために0.57になる可能性がありますが、それは0でも1でもありません。四捨五入するのは良くありません。なぜなら、それは0または1をランダムに選ぶことと同等だからです。
SMOTEが新しいポイントを生成する方法を思い出してみましょう:
- 点x_iに最も近い隣接点z_i1、z_i2、…、z_ikを仮定する
- jは[1、k]のランダムな数とする
- rは[0、1]のランダムな数とする
その後、各点x_iに対して、SMOTEは単純に次のように適用して新しい点x_i’を生成します:

明らかなように、カテゴリ特徴が存在する場合には同じ方法を適用することはできません。そのため、次の2つの質問に答えることで拡張する必要があります。
- k最近傍点はどのように見つけられるのか?ユークリッド距離メトリックは連続特徴のみに作用します。
- 新しい点はどのように生成されるのか?SMOTEの方程式はx_i’のカテゴリ部分を生成するためには適用できません。
最初の質問について、著者はカテゴリ部分を考慮に入れるためにユークリッド距離を変更することを提案しました。x_iとz_ijのそれぞれがm個の連続特徴とn個のカテゴリ特徴を含むと仮定すると、変更されたメトリックでは連続特徴が自然に減算されて二乗され、さらに異なるカテゴリ特徴のペアごとに定数のペナルティが追加されます。このペナルティは特に、アルゴリズムの開始時に計算できるすべての連続特徴の分散の中央値です。
例えば、2点x_1とx_2の距離を測定する場合:

ここで、標準偏差の中央値がmである場合、距離は次のようになります:

最後の2つの項は、最後の2つのカテゴリ特徴が異なることを考慮しています。
著者はこのメトリックの正当化を提供していませんが、カテゴリ特徴の距離を測定する最も一般的な方法の1つがハミング距離であることを観察した後に意味をなすかもしれません。それは、カテゴリ特徴の異なるペアごとに1を追加するだけです。ハミング距離が6である場合、2つの点は6つのカテゴリ特徴で異なる値を持っていることを示しています。私たちの場合、1をペナルティとして設定するのは直感的ではないことは明らかです。なぜなら、連続特徴が強く変動する場合、1は合計にとって非常に無視できるものになるからです。2つの連続特徴間の平均二乗差をペナルティとして使用すると、この問題を回避できるはずです。なぜなら、連続特徴の分散が大きい場合、ペナルティも大きく、無視できないからです。唯一の注意点は、著者が分散の中央値を使用しており、その平均ではないことです。これは外れ値に対する堅牢性によって正当化されるかもしれません。
2番目の質問に答えることは、変更された距離尺度を使用してk最近傍を見つけた後は、非常に簡単です。通常どおり、SMOTEの方程式を使用して新しい点の連続部分を生成することができます。新しい点のカテゴリ部分を生成するためには、k最近傍のカテゴリ部分のモードを単純に取るのが合理的です。つまり、最も一般的な値が優勢になるように、近傍の値がカテゴリ部分で投票します。
したがって、SMOTE-NCが新しい点を生成するために行うことは次の通りです…
- 点のk最近傍を見つける(kはアルゴリズムのハイパーパラメータである)(変更されたユークリッド距離を使用する)
- それらの中からランダムに1つを選ぶ
- 点からその近傍までの連続特徴空間上の線分を引く
- その線分上の点をランダムに選ぶ
- それを新しい点の連続部分とする
- k最近傍のカテゴリ部分のモードを新しい点のカテゴリ部分とする
SMOTE-N(SMOTE-Nominal)
カテゴリ特徴量が関与していない場合、SMOTE-NCはSMOTEになることは明らかです。なぜなら、ペナルティがゼロであり、生成のモードステップがスキップされるからです。ただし、連続特徴量が関与していない場合、アルゴリズムは不安定な状況にあります。なぜなら、連続特徴がないためペナルティが定義されていないからです。回避策として、それを1などに設定し、通常通りにアルゴリズムを操作することもできますが、最近傍の計算時に容易に多くのタイが生じるでしょう。1つの点と別の10の点とのハミング距離が7である場合、それらは本当にその点に等しく近いのでしょうか?それとも、7つの特徴量が異なるという共通点を持っているだけですか?
SMOTE-Nは、純粋にカテゴリカルなデータに対処するために著者が論文で提案している別のアルゴリズムです。イタリック体の質問に否定的に反応し、カテゴリカル特徴量に対して別の距離尺度を使用します。k最近傍が見つかったら、モード計算によって新しい点が決定されます。ただし、この場合、点自体も計算に関与します。
したがって、SMOTE-NでK-NNを実行するために使用される距離尺度を説明するだけで十分です。この尺度は「修正値距離尺度」と呼ばれ、2つの特徴ベクトル間で以下のように動作します。各カテゴリ値を、クラスごとの周波数で全クラスの周波数で割ったKの長さのベクトルVでエンコードします。
- 各カテゴリ値を、Kの長さのベクトルVでエンコードする。ここで、Kはクラスの数です。V[i]はi番目のクラスにおけるその値の周波数を、全クラスの周波数で割ったものです。
- 今や、任意のカテゴリベクトルは、長さkのq個のベクトルのテンソルで表されます。
- そのテンソルで表される任意の2つのカテゴリベクトル間の距離を計算するには、長さkのベクトルの各ペアのマンハッタン距離を計算し、その結果のL2ノルムを取る。
例として、次の2つのカテゴリベクトル間の距離を求めたいとします。

3つのクラスがあると仮定して、それらをエンコードした後、以下のようになるとします。

ベクトルの各ペアのマンハッタン距離を計算すると、以下のようになります。

これにより、L2ノルムを取ると1.428になります。
正確に言うと、論文では大きさにL1ノルムまたはL2ノルムのいずれかを使用することができると指摘していますが、アルゴリズムにどちらを使用するかは決まっていません(ここではL2を選びました)。
なぜこれがプレーンなハミング距離を使用するよりも優れているのか、という質問に対しては、明確な答えは著者自身が正当化していません。ただし、わずかな直感を紹介するために、ハミング距離ではKNNの距離計算中に多くのタイが生じることがしばしばあると述べました。3つのカテゴリベクトルがあると仮定しましょう。

ここでは、ハミング距離はx_2とx_3がx_1にとても近いと示唆しています。なぜなら、両方の場合、ハミング距離は1だからです。一方、修正された値の差異メトリックは、どの値がクラスにどのように分布しているかを見てから、どちらがより近いかを決定します。B2の各クラスの頻度が[0.3、0.2、0.5]であり、B3の頻度が[0.1、0.9、0]であり、B1の頻度が[0.25、0.25、0.5]であるとします。この場合、MVDMはB1がB3よりもB2にはるかに近いため、x_3がx_1にとても近いと示唆します。確率的な観点から言えば、未知のクラスを持つ新しい点を収集する場合、カテゴリがB2またはB3であるかどうかはクラスを予測するのにあまり役に立たず、この意味では似ているか交換可能です。
したがって、SMOTE-Nアルゴリズムの要点は次のとおりです:
- 修正された値の差異メトリックを使用して、点のk個の最近傍を見つける(kはアルゴリズムのハイパーパラメータです)
- 新しい点を生成するために、最近傍(自身の点を含む)のカテゴリ値のモードを返す
以上です!SMOTE、SMOTE-N、SMOTE-NCがそれぞれどのように動作するかが明確になったはずです。次回まで、さようなら。
参考文献:
[1] N. V. Chawla, K. W. Bowyer, L. O.Hall, W. P. Kegelmeyer, “SMOTE: synthetic minority over-sampling technique,” Journal of artificial intelligence research, 321–357, 2002.
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
